湖北省武汉市蔡甸区2021年数学中考二模试卷

试卷更新日期：2021-12-07 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的倒数是（）

A、 $3$ B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、-3

查看试题解析
2. 掷一个质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数.下列事件是必然事件的是（）

A、掷两次骰子，朝上的一面的点数和大于1 B、掷一次骰子，朝上的一面的点数为7 C、掷一次骰子，朝上的一面的点数为4 D、掷两次骰子，朝上的一面的点数都是3

查看试题解析
3. 拼图是一种广受欢迎的智力游戏，需要将形态各异的组件拼接在一起，下列拼图组件是中心对称图形的为（）

A、 B、 C、 D、

查看试题解析
4. 计算 ${(- a^{2})}^{3}$ 的结果是（）

A、 $- a^{6}$ B、 $a^{6}$ C、 $- a^{5}$ D、 $a^{5}$

查看试题解析
5. 如图，是由若干个同样大小的立方体搭成的几何体的俯视图，小正方形中的数字表示该位置立方体的个数，则这个几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
6. 2020年某市初中学业水平实验操作考试，要求每名学生从物理、化学、生物三个学科中随机抽取一科参加测试，小明和小颖都抽到生物学科的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{9}$

查看试题解析
7. 对于函数 $y = \frac{6}{x}$ ，下列说法错误的是（）

A、它的图象分布在一、三象限 B、它的图象既是轴对称图形又是中心对称图形 C、当x>0时，y的值随x的增大而增大 D、当x<0时，y的值随x的增大而减小

查看试题解析
8. 小明同学利用“描点法”画某个一次函数的图象时，列出的部分数据如下表：

$x$

…

-2

-1

0

1

2

…

$y$

…

4

1

-2

-6

-8

…

经过认真检查，发现其中有一个函数值计算错误，这个错误的函数值是（）

A、2 B、1 C、-6 D、-8

查看试题解析
9. 如图， $⊙ O$ 的半径为 $4$ ，点 $P$ 是 $⊙ O$ 外的一点， $P O = 10$ ，点 $A$ 是 $⊙ O$ 上的一个动点，连接 $P A$ ，直线 $l$ 垂直平分 $P A$ ，当直线 $l$ 与 $⊙ O$ 相切时， $P A$ 的长度为（）

A、10 B、 $\frac{21}{2}$ C、11 D、 $\frac{43}{4}$

查看试题解析
10. 在平面直角坐标系中，若一个正比例函数 $y = k x$ 的图象经过 $A (a ， 1)$ ， $B (1 ， b)$ 两点，反比例函数 $y = \frac{m^{2} + m}{x}$ 的图象经过点 $(a ， b)$ ，则 $m - \frac{1}{m}$ 的值为（）

A、-1 B、1 C、±1 D、-2

查看试题解析

二、填空题

11. 计算 $\sqrt{{(- \frac{1}{2})}^{2}}$ 的结果是．

查看试题解析

12. 在一次中学生田径运动会上，参加男子跳高的17名运动员的成绩如下表所示.

成绩/ $m$	1.50	1.60	1.65	1.70	1.75	1.80
人数	1	4	4	5	2	1

则这些运动员成绩的中位数为.

查看试题解析

13. 方程 $\frac{x}{x + 1} = \frac{1}{2 x + 2} + 2$ 的解是

查看试题解析
14. 如图，海上有一灯塔P，位于小岛A北偏东60°方向上，一艘轮船从北小岛A出发，由西向东航行 $24nmile$ 到达B处，这时测得灯塔P在北偏东30°方向上，如果轮船不改变航向继续向东航行，当轮船到达灯塔P的正南方，此时轮船与灯塔P的距离是 $n mile$ .（结果保留一位小数， $\sqrt{3} \approx 1.73$ ）

查看试题解析
15. 如图，已知二次函数y=ax²+bx+c（a≠0）的图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0），下列说法：①bc＜0；② $\frac{c}{a}$ =﹣3；③4a+2b+c＜0；④若t为任意实数，x=﹣1+t时的函数值大于x=﹣1﹣t时的函数值.其中正确的序号是.

查看试题解析
16. 在矩形 $A B C D$ 中， $A B = 3$ ， $B C = 4$ ，点 $E$ 是 $A D$ 上一动点，过点 $E$ 作 $E F // B D$ 交 $A B$ 于 $F$ ，将 $△ A E F$ 沿 $E F$ 折叠，点 $A$ 的对应点 $A^{'}$ 落在 $B C$ 边上时， $A E$ 的长为

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} x - 3 \leq 0 ① \\ 5 (x - 1) + 6 > 4 x ② \end{array}$ 请按下列步骤完成解答：

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来；

(4)、原不等式组的解集为.

查看试题解析
18. 已知 $A B // C D$ ， $E G$ ， $H F$ 分别是 $∠ A E F$ ， $∠ E F D$ 的角平分线.求证： $E G // H F$ .

查看试题解析
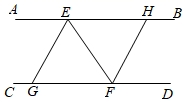19. 随着信息技术的迅猛发展，人们购物的支付方式更加多样、便捷，为调查大学生购物支付方式，某大学一份调查问卷，要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：

(1)、这次活动共调查了人；在扇形统计图中，表示“支付宝”支付的扇形圆心角的度数为

(2)、将条形统计图补充完整；

(3)、若该大学有10000名学生，请你估计购物选择用支付宝支付方式的学生约有多少人？

查看试题解析
20. 如图，在下列 $8 \times 8$ 的网格中，横、纵坐标均为整点的数叫做格点， $△ A B C$ 的顶点的坐标分别为 $A (3 ， 0)$ ， $B (0 ， 4)$ ， $C (4 ， 2)$ .

⑴直接写出 $△ A B C$ 的形状；

⑵要求在下图中仅用无刻度的直尺作图：将 $△ A B C$ 绕点 $B$ 逆时针旋转角度 $2 α$ 得到 $△ A_{1} B C_{1}$ ，其中 $α = ∠ A B C$ ， $A$ ， $C$ 的对应点分别为 $A_{1}$ ， $C_{1}$ ，请你完成作图；

⑶在网格中找一个格点 $G$ ，使得 $C_{1} G ⊥ A B$ ，并直接写出 $G$ 点的坐标；

⑷作点 $C_{1}$ 关于 $B C$ 的对称点 $D$ .

查看试题解析
21. $R t △ A B C$ 中， $∠ C = 90 °$ ， $O$ 为 $A B$ 上一点，以 $O$ 为圆心， $O A$ 为半径的圆与 $B C$ 相切于点 $D$ .

(1)、求证： $A D$ 平分 $∠ B A C$ ；

(2)、连接 $D E$ ，若 $A B = 2 B D$ ，求 $\cos ∠ C D E$ 的值.

查看试题解析
22. 空气净化器越来越被人们认可，某商场购进A、B两种型号的空气净化器，如果销售5台A型和10台B型空气净化器的销售总价为20000元，销售10台A型和5台B型空气净化器的销售总价为17500元.

(1)、求每台A型空气净化器和B型空气净化器的销售单价；

(2)、该商场计划一次购进两种型号的空气净化器共100台，其中B型空气净化器的进货量不超过A型空气净化器的2倍，设购进A型空气净化器 $m$ 台，这100台空气净化器的销售总价最大时，该公司购进A型、B型空气净化器各多少台？

(3)、在（2）的条件下，若A型空气净化器每台的进价为800元，B型空气净化器每台的进价 $z$ （元）满足 $z = - 10 m + 700$ 的关系式，则销售完这批空气净化器能获取的最大利润是多少元？

查看试题解析
23. 如图， $△ A B C$ 中，点 $D$ 在 $B C$ 边上，且 $∠ A D B = 90 ° + \frac{1}{2} ∠ C A D$ .

(1)、求证： $A D = A C$ ；

(2)、点 $E$ 在 $A B$ 边上，连接 $C E$ 交 $A D$ 于点 $F$ ，且 $∠ C F D = ∠ C A B$ ， $A E = B D$ ，
①求 $∠ A B C$ 的度数；

②若 $A B = 8$ ， $D F = 2 A F$ ，直接写出 $E F$ 的长.

查看试题解析
24. 已知抛物线 $C_{1} ： y = a x^{2} - 4 a x + c$ 经过点 $C (4 ， 3)$ ，与 $x$ 轴交于 $A (- 2 ， 0)$ ， $B$ 两点.

(1)、求抛物线 $C_{1}$ 的解析式；

(2)、如图1， $D$ 为抛物线 $C_{1}$ 上 $A$ ， $C$ 之间的动点，过点 $D$ 作 $D E ⊥ x$ 轴于点 $E$ ， $D F ⊥ O C$ 于点 $F$ ，求 $D E + D F$ 的最大值；

(3)、如图2，平移抛物线 $C_{1}$ 的顶点到原点，得到抛物线 $C_{2}$ ，直线 $y = x + b$ 交抛物线 $C_{2}$ 于 $P$ ， $Q$ 两点，已知点 $H (0 ， 1)$ ，连接 $P H$ ， $Q H$ 分别交抛物线 $C_{2}$ 于另一点 $N$ ， $M$ ，求证：直线 $M N$ 经过一个定点.

查看试题解析

$x$	…	-2	-1	0	1	2	…
$y$	…	4	1	-2	-6	-8	…