江苏省无锡市惠山区2021-2022学年七年级上学期数学期中考试试卷

试卷更新日期：2021-12-07 类型：期中考试

进入出卷网下载

一、单选题

1. “疫情防控，我们在一起”：每个人都是疫情防控的重要一环.下面是人民日报发布的疫情防控宣传图，上有图案和文字说明，其中图案是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列根式中是最简二次根式的是（）

A、 $\sqrt{\frac{2}{3}}$ B、 $\sqrt{3}$ C、 $\frac{4}{\sqrt{2}}$ D、 $\sqrt{8}$

查看试题解析
3. 如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（）

A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD

查看试题解析
4. 过点A作直线AB的垂线，符合要求的作图痕迹是（）

A、 B、 C、 D、

查看试题解析
5. “三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角，这个三等分角仪由两根有槽的棒 $O A$ ， $O B$ 组成，两根棒在 $O$ 点相连并可绕 $O$ 转动， $C$ 点固定， $O C = C D = D E$ ，点 $D$ ， $E$ 可在槽中滑动，若 $∠ B D E = 75 °$ ，则 $∠ O$ 的度数是（）

A、 $15 °$ B、 $20 °$ C、 $25 °$ D、 $30 °$

查看试题解析
6. a，b是两个连续整数，若a＜ $\sqrt{5}$ ＜b，则a，b分别是（）

A、1，3 B、3，2 C、2，3 D、3，4

查看试题解析
7. 如图，一根长为a的木棍（AB），斜靠在与地面（OM）垂直的墙上，设木棍的中点为P，若木棍A端沿墙下滑，且B端沿地面向右滑动，在滑动的过程中OP的长度（）

A、减小 B、增大 C、不变 D、先减小再增大

查看试题解析
8. 如图，图中的阴影部分是由5个小正方形组成的一个图形，若在图中的方格里再涂黑一个正方形，使整个阴影部分成为轴对称图形，涂法有（）

A、3种 B、4种 C、5种 D、6种

查看试题解析
9. 小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线.”他这样做的依据是（）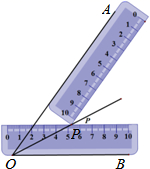

A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确

查看试题解析
10. 如图，在边长为3的正方形ABCD中，请画出以A为一个顶点，另两个顶点在正方形ABCD边上的等腰三角形，且有一条边长为2.满足条件的等腰三角形有（）个.

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

11. 要使二次根式 $\sqrt{x - 3}$ 有意义，则x的取值范围是．

查看试题解析
12. 化简 $\sqrt{12} =$ ．

查看试题解析
13. 2021年10月8日，市场监管总局根据《中华人民共和国反垄断法》的规定，对美团在中国境内网络餐饮外卖平台服务市场滥用市场支配地位的行为处以34.42亿元的罚款，近似数34.42亿精确到位.

查看试题解析
14. 若等腰三角形的一个内角为 50° ，则这个等腰三角形的顶角为.

查看试题解析
15. 有一个数值转换器，原理如图：当输入x为81时，输出的y的值是.

查看试题解析
16. 如图，在锐角△ABC中，∠A=80°，DE和DF分别垂直平分边AB、AC，则∠DBC的度数为°．

查看试题解析
17. 如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，已知EH=EB=3，AE=4，则CH的长是

查看试题解析
18. 如图，在Rt△ABC中，∠BAC=90°，AB=2，M为边BC上的点，连接AM.如果将△ABM沿直线AM翻折后，点B恰好落在边AC的中点处，那么点M到AC的距离是.

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{25} - \sqrt[3]{64} - {(- 1)}^{2021}$ ；

(2)、 $| \sqrt{3} - 2 | - \sqrt{{(- 3)}^{2}} - \sqrt[3]{- 27}$ .

查看试题解析
20. 求下列各式中x的值：

(1)、（x﹣2）²＝4；

(2)、（x+1）³﹣64＝0.

查看试题解析
21. 已知：如图，C是AB的中点，AE＝BD，∠A＝∠B.
求证：∠ACE＝∠BCD.

查看试题解析
22. 阅读下列材料，然后回答问题.
在进行二次根式运算时，形如 $\frac{2}{\sqrt{3} - 1}$ 一样的式子，我们可以将其进一步化简： $\frac{2}{\sqrt{3} - 1}$ ＝ $\frac{2 (\sqrt{3} + 1)}{(\sqrt{3} - 1) (\sqrt{3} + 1)}$ ＝ $\sqrt{3} + 1$ ，以上这种化简的步骤叫做分母有理化.

(1)、请用上述的方法化简 $\frac{2}{\sqrt{7} - \sqrt{5}}$ ；

(2)、利用上面的解法，化简： $\frac{3}{1 + \sqrt{2}} + \frac{3}{\sqrt{2} + \sqrt{3}} + \frac{3}{\sqrt{3} + \sqrt{4}} + \dots + \frac{3}{\sqrt{99} + \sqrt{100}}$ .

查看试题解析
23.

(1)、如图（1），在△ABC，AB=AC，O为△ABC内一点，且OB=OC，求证：直线AO垂直平分BC.以下是小明的证题思路，请补全框图中的分析过程.

要证直线AO垂直平分BC，只要证点A点O都在BC的垂直平分线上，只要证

= ， =

(2)、如图（2），在△ABC中，AB=AC，点D、E分别在AB、AC上，且BD=CE.请你只用无刻度的直尺画出BC边的垂直平分线（不写画法，保留画图痕迹）.

(3)、如图（3），在五边形ABCDE中，AB=AE，BC=DE，∠B=∠E，请你只用无刻度的直尺画出CD边的垂直平分线，并说明理由.

查看试题解析
24. 如图，在△ABC中，点D在AB上，且CD=CB，E为BD的中点，F为AC的中点，连接EF交CD于点M，连接AM.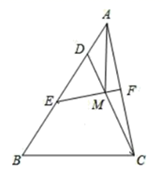

(1)、求证：EF= $\frac{1}{2} A C$ ；

(2)、若EF⊥AC，求证：AM+DM=CB.

查看试题解析
25. 阅读理解：如图1，在△ABC的边AB上取一点P，连接CP，可以把△ABC分成两个三角形，如果这两个三角形都是等腰三角形，我们称点P是△ABC的边AB上的完美点.

解决问题：

(1)、如图2，△ABC中，∠ACB＝90°，试找出边AB上的完美点P，并说明理由.

(2)、如图3，已知∠A＝36°，△ABC的顶点B在射线l上，点P是边AB上的完美点，请认真分析所有符合要求的点B，直接写出相应的∠B的度数.

查看试题解析
26. 在△ABC中，∠BAC＝90°，AB＝AC，∠ABC＝∠ACB＝45°，在△ABC外侧作∠ACM，使得∠ACM＝ $\frac{1}{2}$ ∠ABC，点D是射线CB上的动点，过点D作直线CM的垂线，垂足为E，交直线AC于F.

(1)、当点D与点B重合时，如图1所示，线段DF与EC的数量关系是；

(2)、当点D运动到CB延长线上某一点时，线段DF和EC是否保持上述数量关系？请在图2中画出图形，并说明理由.

查看试题解析