江苏省南通市如皋市2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期:2021-12-07 类型:期中考试
一、单选题
-
1. 在下列“禁毒”“和平”“志愿者”“节水”这四个标志中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 如图, ,点 , , 在同一直线上,若 , ,则 的长为( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 如图, ,点 , , 在同一直线上,若 , ,则 的长为( ) A、3 B、8 C、10 D、114. 如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是( )
A、3 B、8 C、10 D、114. 如图,用纸板挡住部分直角三角形后,能画出与此直角三角形全等的三角形,其全等的依据是( ) A、 B、 C、 D、5. 等边三角形的两条中线相交所成的锐角为( )A、 B、 C、 D、6. 已知 , ,则 的值为( )A、5 B、9 C、13 D、177. 如图,在 中, ,点 是 内一点,且 ,若 ,则 的度数为( )
A、 B、 C、 D、5. 等边三角形的两条中线相交所成的锐角为( )A、 B、 C、 D、6. 已知 , ,则 的值为( )A、5 B、9 C、13 D、177. 如图,在 中, ,点 是 内一点,且 ,若 ,则 的度数为( )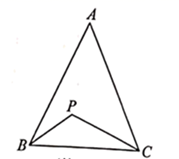 A、 B、 C、 D、8. 如图,在 中, ,点 在边 上,且 ,若 , ,则 的长为( )
A、 B、 C、 D、8. 如图,在 中, ,点 在边 上,且 ,若 , ,则 的长为( ) A、3 B、2.5 C、2 D、19. 如图,已知Rt△OAB,∠OAB=50°,∠AOB=90°,O点与坐标系原点重合,若点P在x轴上,且△APB是等腰三角形,则点P的坐标可能有( ).
A、3 B、2.5 C、2 D、19. 如图,已知Rt△OAB,∠OAB=50°,∠AOB=90°,O点与坐标系原点重合,若点P在x轴上,且△APB是等腰三角形,则点P的坐标可能有( ).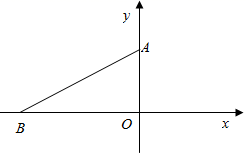 A、1个 B、2个 C、3个 D、4个10. 定义关于 , 的新运算: ,其中 , 为正整数.例如,已知 ,则 .若 ,则 的结果为( )A、 B、 C、 D、
A、1个 B、2个 C、3个 D、4个10. 定义关于 , 的新运算: ,其中 , 为正整数.例如,已知 ,则 .若 ,则 的结果为( )A、 B、 C、 D、二、填空题
-
11. 点 关于 轴对称的点的坐标为.12. 计算: .13. 如图, 中, , , 平分 ,交 于点 .若 ,则 的长为.
 14. 如图,在 中,直线 垂直平分 ,垂足为 ,交 于点 ,若 的周长为 , ,则 的长为.
14. 如图,在 中,直线 垂直平分 ,垂足为 ,交 于点 ,若 的周长为 , ,则 的长为. 15. 如图,小明用 块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放一个等腰直角三角尺 ,点 在 上,点 , 分别与木墙的顶端重合,则两堵木墙之间的距离为 .
15. 如图,小明用 块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放一个等腰直角三角尺 ,点 在 上,点 , 分别与木墙的顶端重合,则两堵木墙之间的距离为 . 16. 如图,在 中, , , ,以A为圆心,以适当的长为半径作弧,交 于点 ,交 于点 .分别以 , 为圆心,以大于 的长为半径作弧,两弧在 的内部相交于点 ,作射线 ,交 于点 ,点 在 边上, ,连接 ,则 的周长为.
16. 如图,在 中, , , ,以A为圆心,以适当的长为半径作弧,交 于点 ,交 于点 .分别以 , 为圆心,以大于 的长为半径作弧,两弧在 的内部相交于点 ,作射线 ,交 于点 ,点 在 边上, ,连接 ,则 的周长为.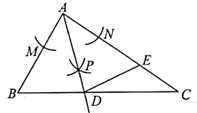 17. 小丽在计算 时,把 写成 后,发现可以连续运用平方差公式进行计算.用类似方法计算: .18. 如图, , 在 的同侧, , , ,点 为 的中点,连接 , , ,若 ,则 的最大值为.
17. 小丽在计算 时,把 写成 后,发现可以连续运用平方差公式进行计算.用类似方法计算: .18. 如图, , 在 的同侧, , , ,点 为 的中点,连接 , , ,若 ,则 的最大值为.
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 先化简,再求值: ,其中 , .21. 如图①、图②、图③都是 的正方形网格,每个小正方形的顶点称为格点.A, ,C均为格点.在给定的网格中,按下列要求画图:
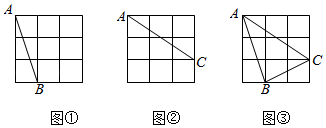 (1)、在图①中,画一条不与 重合的线段 ,使 与 关于某条直线对称,且M,N为格点.(2)、在图②中,画一条不与 重合的线段 ,使 与 关于某条直线对称,且P,Q为格点.(3)、在图③中,画一个 ,使 与 关于某条直线对称,且D,E,F为格点.22. 已知AB=AC,BD=CE,求证:∠B=∠C.
(1)、在图①中,画一条不与 重合的线段 ,使 与 关于某条直线对称,且M,N为格点.(2)、在图②中,画一条不与 重合的线段 ,使 与 关于某条直线对称,且P,Q为格点.(3)、在图③中,画一个 ,使 与 关于某条直线对称,且D,E,F为格点.22. 已知AB=AC,BD=CE,求证:∠B=∠C. 23. 已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、 D.求证:PC=PD.
23. 已知:∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM上滑动,两直角边分别与OA、OB交于C、 D.求证:PC=PD. 24. 如图,正方形 的边长为 ,点 在 上,四边形 是边长为 的正方形,连接 , .
24. 如图,正方形 的边长为 ,点 在 上,四边形 是边长为 的正方形,连接 , . (1)、用含 , 的代数式表示: , 的面积=;(2)、若 的面积为 ,两个正方形的面积之和为60,求 的长.25. 在等边 的两边 , 所在直线上分别有两点 , ,点 为 外一点,且 , , .(1)、如图1,点 , 在边 , 上, ,求 的长;
(1)、用含 , 的代数式表示: , 的面积=;(2)、若 的面积为 ,两个正方形的面积之和为60,求 的长.25. 在等边 的两边 , 所在直线上分别有两点 , ,点 为 外一点,且 , , .(1)、如图1,点 , 在边 , 上, ,求 的长; (2)、如图2,点 , 在边 , 上, ,试猜想 , , 之间的数量关系,并加以证明;
(2)、如图2,点 , 在边 , 上, ,试猜想 , , 之间的数量关系,并加以证明;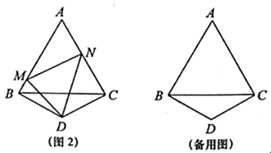 (3)、当点 , 在 , 的延长线上时,若等边 的周长为 , 的长为 ,则 的周长为(用含有 , 的代数式表示).26. 如图
(3)、当点 , 在 , 的延长线上时,若等边 的周长为 , 的长为 ,则 的周长为(用含有 , 的代数式表示).26. 如图
(了解概念)如图1,已知 , 为直线 同侧的两点,点 为直线 的一点,连接 , ,若 ,则称点 为点 , 关于直线 的“等角点”.
(1)、(理解运用)如图2,在 中, 为 上一点,且与点 关于直线 对称,连接 并延长至点 ,判断点 是否为点 , 关于直线 的“等角点”,并说明理由;
(2)、(拓展提升)如图2,在(1)的条件下,若 , ,点 是射线 上一点,且点 , 关于直线 的“等角点”为点 ,请利用尺规在图2中确定点 的位置,并求出 的度数;
(3)、如图3,在 中, , 的平分线交于点 ,点 到 的距离为 ,直线 垂直平分边 ,点 为点 , 关于直线 的“等角点”,连接 , ,当 时, 的值为.