浙教版数学七上第5章 一元一次方程 优生综合题特训
试卷更新日期：2021-12-07 类型：复习试卷
一、综合题
-
1.(1)、几个人共同种一批树苗，如果每入种13棵，则缺4棵树苗：如果每人种11棵，又剩下6棵树苗未种。求这批树苗的棵数．(2)、小红：我不小心把老师留的作业题弄丢了，只记得式子是8-a+b-c．小明：我告诉你，a的相反数是-3，b的绝对值是7，c的相反数和绝对值都是它本身。请根据对话求8-a+b-c的值．2. 在数轴上点A表示数a ， 点B表示数b ， 点C表示数c；a是最大的负整数，a、b、c满足|a+b|+（c﹣5）2＝0．
(1)、填空：a＝ ， b＝ ， c＝；(2)、P为数轴上一动点，其对应的数是x ， 当P在线段AC上，且PA+PB+PC＝7时，求x的值．(3)、若点P ， Q分别从A ， C同时出发，匀速相向运动，点P的速度为3个单位/秒，点Q的速度为1个单位/秒．当点P运动到C后迅速以原速返回A；点Q运动至B点后停止运动，同时P点也停止运动．求在此运动过程中P ， Q的相遇点在数轴上对应的数．3. 某市为鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过40立方米时，按2元/立方米计费；月用水量超过40立方米时，其中的40立方米仍按2元/立方米收费，超过部分按3元/立方米计费．(1)、小华家四月份用水26立方米，五月份用水52立方米，请帮小华计算一下他家这两个月一共应交多少元水费？(2)、小华家六月份交水费170元，请帮小华计算一下他家这个月用水量多少立方米？4. 如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB＝14．动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．
(1)、写出数轴上点B表示的数 ， 点P表示的数（用含t的代数式表示）；(2)、动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？(3)、若点D是数轴上一点，点D表示的数是x ， 请你探索式子|x+6|+|x﹣8|是否有最小值？如果有，直接写出最小值；如果没有，说明理由．5. 如图所示，观察数轴，请回答．
(1)、点C与点D的距离为 ， 点B与点D的距离为；点B与点E的距离为 ， 点C与点A的距离为；(2)、发现：在数轴上，如果点M与点N分别表示数m ， n ， 则它们之间的距离可表示为MN=（用m ， n表示）；(3)、利用发现的结论，逆向思维解决下列问题：①数轴上表示x的点P与 B之间的距离是1，则x的值是 ▲ ；
②|x+3|=2，则x= ▲ ；
③数轴上是否存在点P ， 使点P到点B、点C的距离之和为11？若存在，请求出x的值；若不存在，说明理由．
6. 如图，已知线段AB ， 按下列要求完成画图和计算：
(1)、延长线段AB到点C ， 使BC＝3AB（尺规作图，不写作法，保留作图痕迹）；(2)、在（1）的条件下，如果点D为线段BC的中点，且AB＝2，求线段AD的长度；(3)、在以上的条件下，若点P从A点出发，以每秒1个单位长度的速度向点C移动，到点C时停止．设点P的运动时间为t秒，是否存在某时刻t ， 使得PB＝PA﹣PC？若存在，求出时间t：若不存在，请说明理由．7. 数轴上有A、B、C三个小球，分别对应的数是a、b、c，且满足a是绝对值最小的正整数，B球在原点的左侧且到原点的距离是5，C球在A球的右侧，且到B球的距离是到A球距离的4倍，三个球都在数轴上同时开始运动，A球向左运动，运动速度为每秒2个单位长度，B、C两球向右运动，运动速度分别为每秒4个单位长度和1个单位长度.(1)、a=；b=；c=.(2)、小球A碰到B后按原来的速度立刻返回，B球仍按原速原方向继续前行，请问：小球A在何时何地遇到小球B；当B追上C时停止运动，此时A球所在的位置在哪里？（要有解答过程）
(3)、在（2）的条件下，整个运动过程中何时三个球中的一个球到另外两个球的距离相等.（直接写出结果）.8. 周末小甬陪爸爸去陶瓷商城购买一些茶壶和一些茶杯了了解情况后发现甲、乙两家商店都 在出售两种同样品牌的茶壶和茶杯， 定价相同，茶显每把定价40元，茶杯每只定价5元，且两家 都有优惠，甲商店买一送一大酬宾(买一把茶壶送一只茶杯)，乙商店全场九折，小甬的爸爸需茶壸 5把，茶杯 只(不少于 5 只).(1)、分别用含有 的代数式表示在甲、乙两家商店购买所需的费用；(2)、当 时， 在甲、乙哪个商店购买付款较少? 请说明理由；(3)、若小甬的爸爸准备了1800元钱，在甲、乙哪个商店购买的茶杯多?请说明理由.9. 如图，数轴上有两点A、B，对应的数分别为-4，2，点P为数轴上一动点，其对应的数为x.
(1)、若点P到点A、点B的距离相等，求点P对应的x的值.(2)、数轴上是否存在点P，使得点P到点A、点B的距离之和为8？若存在，请求出x的值；若不存在，说明理由.(3)、点A、B分别以2个单位长度/分，1个单位长度/分的速度向右运动，同时点P以2.5个单位长度/分的速度从O点向左运动，当遇到A时，点P立即以同样的速度向右运动，并不停往返于点A与点B之间，当点A与点B重合时，A、B、P同时停止运动，求此过程中点P所经过的总路程是多少？10. 如图，已知数轴上有 三点，分别表示有理数 ，动点 从点 出发，以每秒1个单位的速度向终点 移动，当点 运动到 点时，点 从 点出发，以每秒3个单位的速度向 点运动.
(1)、 点出发3秒后所到的点表示的数为 ， 此时 两点的距离为.(2)、问当点 从点 点出发几秒钟时，能追上点 ？(3)、问当点 从点 点出发几秒钟时，点 和点 相距2个单位长度？直接写出此时点 在数轴上表示的有理数.11. 解方程：(1)、(2)、12. 如图，在数轴上，点A，B表示的数分别为 ，2，线段AB的中点为M.点P以2个单位长度/秒的速度从点A出发，向数轴的正方向运动.同时，动点Q以1个单位长度/秒的速度从点B出发，向数轴的负方向运动.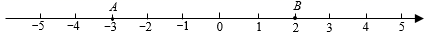
(1)、线段AB的长度为个单位长度，点M表示的数为.(2)、当点Q运动到点M时，点P运动到点N，则MN的长度为个单位长度.(3)、设点P运动的时间为t秒.是否存在这样的t，使PA+QA为7个单位长度？如果存在，请求出t的值和此时点P表示的数；如果不存在，请说明理由.13. 肖坝社区惠民水果店第一次用615元从水果批发市场购进甲、乙两种不同品种的苹果，其中甲种苹果的重量比乙种苹果重量的2倍多15千克，甲、乙两种苹果的进价和售价如下表：甲
乙
进价（元/千克）
5
8
售价（元/千克）
10
15
(1)、惠民水果店第一次购进的甲、乙两种苹果各多少千克？(2)、惠民水果店第二次以第一次的进价又购进甲、乙两种苹果，其中甲种苹果的重量不变，乙种苹果的重量是第一次的3倍；甲种苹果按原价销售，乙种苹果打折销售．第二次甲、乙两种苹果都售完后获得的总利润为735元，求第二次乙种苹果按原价打几折销售？14. 如图所示，数轴上一动点A向左移动2个单位长度到达点B，再向右移动5个单位长度到达点C点.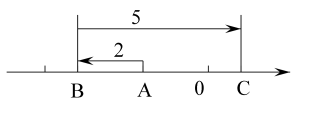
(1)、求动点A所走过的路程及A、C之间的距离.(2)、若C表示的数为1，则点A表示的数为.15. 如图，已知数轴上点A表示的数为8，B是数轴上一点，且AB=14．动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．
(1)、写出数轴上点B表示的数 ， 点P表示的数（用含t的代数式表示）；(2)、动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时追上点Q？(3)、若点D是数轴上一点，点D表示的数是x，请你探索式子 是否有最小值？如果有，直接写出最小值；如果没有，说明理由．16. 如图一根木棒放在数轴上，数轴的1个单位长度为1cm，木棒的左端与数轴上的点A重合，右端与点B重合．
(1)、若将木棒沿数轴向右水平移动，则当它的左端移动到点B时，它的右端在数轴上所对应的数为20；若将木棒沿数轴向左水平移动，则当它的右端移动到A点时，则它的左端在数轴上所对应的数为5，由此可得到木棒长为cm．(2)、图中点A所表示的数是 ， 点B所表示的数是 ．(3)、由题（1）（2）的启发，请你能借助“数轴”这个工具帮助小红解决下列问题：一天，小红去问曾当过数学老师现在退休在家的爷爷的年龄，爷爷说：“我若是你现在这么大，你还要40年才出生；你若是我现在这么大，我已经122岁，是老寿星了，哈哈！”，请求出爷爷现在多少岁了？
17. 某工厂车间有28个工人，生产 零件和 零件，每人每天可生产 零件18个或 零件12个（每人每天只能生产一种零件），一个 零件配两个 零件，且每天生产的 零件和 零件恰好配套．工厂将零件批发给商场时，每个 零件可获利10元，每个 零件可获利5元．(1)、求该工厂有多少工人生产 零件？(2)、因市场需求，该工厂每天要多生产出一部分 零件供商场零售使用，现从生产 零件的工人中调出多少名工人生产 零件，才能使每日生产的零件总获利比调动前多600元？18. 平移和翻折是初中数学两种重要的图形变化(1)、平移运动①把笔尖放在数轴的原点处，先向负方向移动3个单位长度，再向正方向移动2个单位长度，这时笔尖的位置表示什么数？
用算式表示以上过程及结果是.
． ． ． ．
②一机器人从原点 开始，第1次向左跳1个单位，紧接着第2次向右跳2个单位，第3次向左跳3个单位，第4次向右跳4个单位， ，依次规律跳，当它跳2021次时，落在数轴上的点表示的数是 ．
(2)、翻折变换：①若折叠纸条，表示-1的点与表示3的点重合，则表示2021的点与表示的点重合；
②若数轴上 、 两点之间的距离为2022（A在 的左侧，且折痕与①折痕相同），且 、 两点经折叠后重合，则 点表示 ， 点表示 ．
③若数轴上折叠重合的两点的数分别为a、b ，折叠中间点表示的数为 ． （用含有a、b 的式子表示）
19. 公园门票价格规定如下表：购票张数
张
张
张以上
每张票的价格
元
元
元
某校七年级（1）（2）两个班共 人去游园其中（1）班有 多人，不足 人，经估算，如果两个班都以班为单位各自购票，则一共应付 元．
(1)、如果两班联合起来，作为一个团体购票，可省多少钱．(2)、求两班各有多少学生．(3)、如果七年级（1）班单独组织去游园，如果你作为组织者如何购票最省钱，通过计算说明理由．20. 暑假期间德强学校准备粉刷教学楼，粉刷总面积为 平方米，甲、乙两个装饰公司承担了该粉刷任务，已知甲装饰公司每名工人每天粉刷的面积比乙装饰公司每名工人每天粉刷的面积多 平方米，甲装饰公司 名工人一天粉刷的面积等于乙装饰公司 名工人一天粉刷的面积．(1)、求乙装饰公司每名工人每天粉刷面积多少平方米．(2)、若乙装饰公司参与粉刷教学楼的工人比甲装饰公司参与粉刷教学楼的工人多 人，甲装饰公司每天比乙装饰公司多粉刷 ，求甲装饰公司有多少人参与粉刷教学楼．(3)、在（2）的条件下，甲、乙两个装饰公司合作粉刷 天后，因乙装饰公司另有任务调走了部分工人去外地，同时甲装饰公司调来了 台机器人参与粉刷教学楼，此机器人每天粉刷 平方米，由于某种原因甲装饰公司工人的工作效率降低了 ，乙装饰公司未被调走的工人工作效率不变，结果恰好按原计划时间完成粉刷任务，若甲、乙两个装饰公司粉刷费用均为 元/平方米，求甲、乙两个装饰公司各自应获得粉刷费用多少元．21. 某种产品的形状是长方体，长为 ，它的展开图如图：
(1)、求该长方体的宽和高；(2)、某厂家要为该产品做一个包装纸箱，使每箱能装2件这种产品，并且要求没有空隙且要使该纸箱所用材料尽可能少（厚度忽略不计），请求出该纸箱的体积.22. 小林和小明设计了一个小游戏程序：开始时两人的屏幕上显示的数分别是a和 ，每按一次屏幕，小林的屏幕上的数就会加上a，同时小明的屏幕上的数就会加上1，且均显示化简后的结果．如下表就是按一次后及两次后屏幕显示的结果．开始数
按1次后
按2次后
按3次后
按4次后
按5次后
小林
a
小明
根据以上的信息回答问题：
(1)、从开始起按5次后，①两人屏幕上显示的结果是：小林 ▲ ；小明 ▲ ；
②判断这两个结果的大小，并说明理由．
(2)、是否存在一个a的值，使得每次按完屏幕后，小林的屏幕上的数，总是小于小明的屏幕上的数，若存在，请直接写出所有满足条件的a的取值范围；若不存在，请说明理由23. 已知A，B两地之间有一条长240千米的公路．甲车从A地出发匀速开往B地，甲车出发两小时后，乙车从B地出发匀速开往A地，两车同时到达各自的目的地．两车行驶的路程之和y(千米)与甲车行驶的时间x(时)之间的函数关系如图所示．
(1)、甲车的速度为千米/时，a的值为(2)、求乙车的速度．(3)、当甲、乙两车相距100千米时，求甲车行驶的时间．24. 某县2021以来受持续干旱影响，河道来水偏少，已严重影响生产和生活用水，自来水厂推行阶梯水价，引导人们节约用水，调整后的用水价格如下：每月用水量（吨）
单价（元/吨）
不超过20的部分
1.5
超过20不超过30的部分
2
超过30的部分
3
(1)、小明家5月份的用水量为23吨，小明家5月份的水费是多少？(2)、小明家1月份水费的均价为1.75元/吨，求小明家1月份的用水量？(3)、小明家3、4两个月的总用水量为56吨（4月份用水较少），3、4两个月的水费合计93元，请问小明家3、4月份的用水量分别是多少？