浙教版数学七上第3章实数优生综合题特训

试卷更新日期：2021-12-07 类型：复习试卷

进入出卷网下载

一、综合题

1. 阅读下面的文字，解答问题：
大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部地写出来，于是小明用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：∵ $\sqrt{4}$ ＜ $\sqrt{7}$ ＜ $\sqrt{9}$ ，即2＜ $\sqrt{7}$ ＜3，∴ $\sqrt{7}$ 的整数部分为2，小数部分为（ $\sqrt{7}$ ﹣2）．

请解答：

(1)、 $\sqrt{15}$ 的整数部分是，小数部分是；

(2)、已知（ $2 + \sqrt{6}$ ）的小数部分为 $a$ ，（ $5 - \sqrt{6}$ ）的小数部分为 $b$ ，计算 $a + b$ 的值．

查看试题解析
2. 如图1，这是由8个同样大小的立方体组成的魔方，体积为64．

(1)、求出这个魔方的棱长．

(2)、图中阴影部分是一个正方形ABCD，求出阴影部分的面积及其边长．

(3)、把正方形ABCD放到数轴上，如图2，使得A与﹣1重合，那么D在数轴上表示的数为．

查看试题解析
3. 因为 $\sqrt{1} < \sqrt{3} < \sqrt{4}$ ，即 $1 < \sqrt{3} < 2$ ，所以 $\sqrt{3}$ 的整数部分为1，小数部分为 $\sqrt{3} - 1$ ．类比以上推理解答下列问题：

(1)、求 $\sqrt{11}$ 的整数部分和小数部分．

(2)、若m是 $11 - \sqrt{11}$ 的小数部分，n是 $11 + \sqrt{11}$ 的小数部分，且 ${(x + 1)}^{2} = m + n$ ，求x的值．

查看试题解析
4. 下列8个实数：－2，0， $\sqrt{3}$ ， $\sqrt{9}$ ， $\frac{1}{3}$ ，(－2)³ ， (－3)² ， π．

(1)、属于无理数的有：；
属于负整数的有：．

(2)、求题中所列8个实数中的最大数与最小数的乘积．

查看试题解析
5. 已知a，b分别是4+ $\sqrt{3}$ 的整数部分和小数部分．

(1)、分别写出a，b的值；

(2)、求b²+2a的值．

查看试题解析
6. 阅读下列信息材料：
信息1：因为无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来比如：π、 $\sqrt{2}$ 等，而常用的“…”或者“≈”的表示方法都不够百分百准确.

信息2：2.5的整数部分是2，小数部分是0.5，可以看成2.5﹣2得来的；

信息3：任何一个无理数，都可以夹在两个相邻的整数之间，如2＜ $\sqrt{5}$ ＜3，是因为 $\sqrt{4}$ ＜ $\sqrt{5}$ ＜ $\sqrt{9}$ ：根据上述信息，回答下列问题：

(1)、 $\sqrt{13}$ 的整数部分是，小数部分是.

(2)、10+ $\sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为a＜10+ $\sqrt{3}$ ＜b则a+b＝.

(3)、若 $\sqrt{30}$ ﹣3＝x+y，其中x是整数，且0＜y＜1，请求x﹣y的相反数.

查看试题解析
7. 若 $\frac{a}{3}$ 和 $\frac{2 a - 9}{3}$ 是某数的平方根．

(1)、求a的值；

(2)、求这个数的平方根．

查看试题解析
8. 已知 $2 a + 3$ 的立方根是3， $a + b - 1$ 的算术平方根是4， $c$ 是 $\sqrt{11}$ 的整数部分．

(1)、求 $a$ ， $b$ ， $c$ 的值．

(2)、求 $a - 4 b + 3 c$ 的平方根．

查看试题解析
9. 阅读材料： $∵ 2 < \sqrt{6} < 3 ， ∴ \sqrt{6}$ 的整数部分为2， $\sqrt{6}$ 的小数部分为 $\sqrt{6} - 2$ .
解决问题：

(1)、填空： $\sqrt{73}$ 的小数部分是；

(2)、已知a是 $\sqrt{19} - 4$ 的整数部分，b是 $\sqrt{19} - 4$ 的小数部分，求代数式 ${(a + 1)}^{3} + {(b + 4)}^{2}$ 的值；

(3)、已知：m是 $2 + \sqrt{3}$ 的整数部分，n是其小数部分，求 $m - n$ 的相反数.

查看试题解析
10. 已知2a+3的立方根是3，a+b﹣1的算术平方根是4，c是 $\sqrt{11}$ 的整数部分.

(1)、求a，b，c的值.

(2)、求a﹣4b+3c的平方根.

查看试题解析
11. 若一个数m的两个不同的平方根是2a+22和3a-7．

(1)、求这个数m；

(2)、求 $\sqrt{19 + a}$ 的平方根．

查看试题解析
12. 求下列各数的平方根．

(1)、( $- \frac{5}{4}$ )²

(2)、 $\sqrt{441}$

查看试题解析
13. 求下列各数的立方根：

(1)、 $- \frac{125}{512}$

(2)、27

(3)、-0.000 729

查看试题解析
14. 在数轴上表示出下列无理数．

(1)、 $- \sqrt{10}$ ；

(2)、 $\sqrt{8}$

查看试题解析
15. 如图所示，直径为1的圆从原点沿数轴向左滚动一周，圆上与原点重合的点O到达O'，设点O'表示的数为a。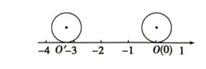

(1)、求a的值。

(2)、求-(a- $\sqrt{16}$ )-π的算术平方根。

查看试题解析
16.

(1)、计算： $\sqrt{36} - \sqrt{{(- 3)}^{2}} + \sqrt{\frac{1}{4}} -^{3} \sqrt{8}$

(2)、计算： $| \sqrt{3} - 2 | - | \sqrt{2} - 1 | + | \sqrt{2} - \sqrt{3} |$

(3)、已知(2x-1)²-9=0，求x的值

查看试题解析

17. 根据下表回答下列问题：

x	16.0	16.1	16.2	16.3	16.4	16.5	16.6	16.7	16.8	16.9	17.0
x²	256.00	259.21	262.44	265.69	268.96	272.25	275.56	278.89	282.24	285.61	289.00

(1)、268.96的平方根是多少？

(2)、

\sqrt{270}

在表中的哪两个数之间？为什么？

(3)、表中与

\sqrt{260}

最接近的是哪个数？

查看试题解析

18. 求下列各式中x的值：

(1)、(2x-1)³-27=0；

(2)、(x+3)²=16．

查看试题解析
19. 通过估算比较大小：

(1)、 $\frac{\sqrt{99} - 7}{2}$ 与 $\frac{8}{5}$ ；

(2)、 $\frac{^{3} \sqrt{10} - 7}{3}$ 与 $\frac{1}{3}$

查看试题解析
20. 喜欢探索数学知识的小明遇到一个新的定义：对于三个互不相等的正整数，若其中任意两个数乘积的算术平方根都是整数，则称这三个数为“老根数”，其结果中最小的整数称为“最小算术平方根”，最大的整数称为“最大算术平方根”.例如：1，4，9这三个数， $\sqrt{1 \times 4}$ ＝2， $\sqrt{1 \times 9}$ ＝3， $\sqrt{4 \times 9}$ ＝6，其结果分别为2，3，6都是整数，所以1，4，9这三个数称为“老根数”，其中“最小算术平方根”是2，“最大算术平方根”是6.

(1)、请证明：2，8，50这三个数是“老根数”，并求出任意两个数乘积的最小算术平方根与最大算术平方根；

(2)、已知16，a，36这三个数是“老根数”，且任意两个数乘积的算术平方根中，最大算术平方根是最小算术平方根的2倍，求a的值.

查看试题解析

21. 根据下表回答问题：

$x$	16	16.1	16.2	16.3	16.4	16.5	16.6	16.7	16.8
$x^{2}$	256	259.21	262.44	265.69	268.96	272.25	275.56	278.89	282.24

(1)、265.69的平方根是；

(2)、

\sqrt{262.44} =

，

\sqrt{28224} =

，

\sqrt{2.5921} =

；

(3)、设

\sqrt{270}

的整数部分为

a

，求

- 4 a

的立方根.

查看试题解析

22. 一个正数 $x$ 的两个不同的平方根分别是 $2 a - 1$ 和 $- a + 2$ ．

(1)、求 $a$ 和 $x$ 的值；

(2)、求 $3 x + 2 a$ 的平方根．

查看试题解析

浙教版数学七上第3章 实数 优生综合题特训

一、综合题

浙教版数学七上第3章实数优生综合题特训