浙教版数学七上第2章有理数的运算优生综合题特训-在线组卷题库

1. 阅读下面文字．

对于 $(- 5 \frac{5}{6}) + (- 9 \frac{2}{3}) + 17 \frac{3}{4} + (- 3 \frac{1}{2})$ 可以如下计算：

原式 $= [(- 5) + (- \frac{5}{6})] + [(- 9) + (- \frac{2}{3})] + (17 + \frac{3}{4}) + [(- 3) + (- \frac{1}{2})]$

$= [(- 5) + (- 9) + 17 + (- 3)] + [(- \frac{5}{6}) + (- \frac{2}{3}) + \frac{3}{4} + (- \frac{1}{2})]$

$= 0 + (- 1 \frac{1}{4})$ $= - 1 \frac{1}{4}$

上面这种方法叫拆项法，类比上面的方法计算．

(1)、

(- 2020 \frac{2}{3}) + 2019 \frac{3}{4} + (- 2018 \frac{5}{6}) + 2017 \frac{1}{2}

；

(2)、

(- 1 \frac{1}{2}) + (- 2000 \frac{5}{6}) + 4000 \frac{3}{4} + (- 1999 \frac{2}{3})

．

查看试题解析

2. 有理数a、b、c在数轴上的位置如图，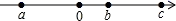

(1)、判断正负，用“＞”或“＜”填空：c－b0，a＋b0，a－c0.

(2)、化简：|c－b|＋|a＋b|－2|a－c|.

查看试题解析

3. 有理数a、b、c在数轴上的位置如图，

(1)、用“＞”或“＜”填空：c－b0，a＋b0，a－c0；

(2)、化简：|c－b|＋2|a＋b|－|a－c|.

查看试题解析

4. 将连续的偶数2，4，6，8，…排成如下表，并用一个十字形框架框住其中的五个数，请你仔细观察十字形框架中的数字的规律，并回答下列问题：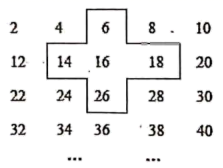

(1)、十字框中的五个数的和等于 .

(2)、若将十字框上下左右移动，可框住另外的五个数，设中间的数为x，用代数式表示十字框中的五个数的和是 .

(3)、在移动十字框的过程中，若框住的五个数的和等于2020，这五个数从小到大依次，，，， .

(4)、框住的五个数的和能等于2019吗？

查看试题解析

5. 观察下面三行数：

﹣2，4，﹣8，16，﹣32，64 …①

0，6，﹣6，18，﹣30，66…②

﹣1，2，﹣4，8，﹣16，32…③

(1)、第①行数按什么规律排列？

(2)、第②③行数与第①行数有什么关系？

(3)、取每行数的第十个数，计算这三个数的和.

查看试题解析

6. 计算：

(1)、计算：12﹣(-6)+(﹣7)-15

(2)、计算：﹣5+（-12）-11-|﹣

\frac{1}{2}

|

(3)、计算：（-2）³+（-3）×[

{(- \frac{1}{2})}^{2}

×4]÷（﹣2）

(4)、﹣1²⁰²¹+

\frac{5}{2}

÷

\frac{5}{8}

﹣

\frac{2}{3}

×（﹣18）

(5)、观察下列各式：

- $1 \times \frac{1}{2}$ =-1+ $\frac{1}{2}$ ，- $\frac{1}{2} \times \frac{1}{3} =$ - $\frac{1}{2} + \frac{1}{3}$ ，- $\frac{1}{3} \times \frac{1}{4} =$ - $\frac{1}{3} + \frac{1}{4}$ ，……

①根据上述规律写出第5个等式是 ▲ ；

②规律应用：计算（- $1 \times \frac{1}{2}$ ）+（- $\frac{1}{2} \times \frac{1}{3}$ ）+（- $\frac{1}{3} \times \frac{1}{4}$ ）+…+（- $\frac{1}{2020} \times \frac{1}{2021}$ ）

③拓展应用：（直接写出结果）

$1 \times \frac{1}{3}$ + $\frac{1}{3} \times \frac{1}{5}$ + $\frac{1}{5} \times \frac{1}{7}$ +…+ $\frac{1}{2019} \times \frac{1}{2021}$ = ▲

查看试题解析

7. 阅读：已知正整数a、b、c ，显然，当同底数时，指数大的幂也大，若对于同指数，不同底数的两个幂

a^{b}

和

c^{b}

，当

a > c

时，则有

a^{b} > c^{b}

，根据上述材料，回答下列问题．

(1)、比较大小：

5^{20}

4^{20}

（填写>、<或=）．

(2)、比较

2^{33}

与

3^{22}

的大小（写出比较的具体过程）．

(3)、计算

4^{2021} \times {0.25}^{2020} - 8^{2021} \times {0.125}^{2020}

．

查看试题解析

8. 下面是小明的计算过程，请仔细阅读．

计算：（–15）÷（ $\frac{1}{3}$ –3– $\frac{2}{3}$ ）×6．

解：原式=（–15）÷（– $\frac{25}{6}$ ）×6…………第一步

=（–15）÷（–25）…………第二步

= $- \frac{3}{5}$ …………第三步

并解答下列问题．

(1)、解答过程是否有错？若有在第几步，并说明不符合题意原因；

(2)、请写出正确的计算过程．

查看试题解析

9. 数学老师布置了一道思考题“计算：（

- \frac{1}{12}

）

\div (\frac{1}{3} - \frac{5}{6})

”，小明仔细思考了一番，用了一种不同的方法解决了这个问题．

小明的解法：原式的倒数为（ $\frac{1}{3} - \frac{5}{6}$ ） $\div (- \frac{1}{12}) =$ （ $\frac{1}{3} - \frac{5}{6}$ ）×（﹣12）＝﹣4+10＝6，

所以（ $- \frac{1}{12}$ ） $\div (\frac{1}{3} - \frac{5}{6}) = \frac{1}{6}$ ．

(1)、请你判断小明的解答是否正确，并说明理由．

(2)、请你运用小明的解法解答下面的问题．

计算：（ $- \frac{1}{24}$ ） $\div (\frac{1}{3} - \frac{1}{6} + \frac{3}{8})$ ．

查看试题解析

10. 已知五个数分别为：

- 5 ， | - 1.5 | ， 0 ， - 3 \frac{1}{2} ， - (- 2) ， 5 ， - 2

(1)、在数轴上表示下列各数，并按从小到大的顺序用“<”把这些数连接起来；

(2)、选择哪三个数相乘可得到最大乘积？乘积最大的是多少？

查看试题解析

11. 概念学习

规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等，类比有理数的乘方，我们把2÷2÷2记作2₃ ，读作“2的3次商”，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）记作（﹣3）₄ ，读作“﹣3的4次商”.一般地，我们把n个a（a≠0）相除记作a_n ，读作“a的n次商”.

(1)、初步探究
直接写出结果：2₃＝；

(2)、关于除方，下列说法错误的是；

①任何非零数的2次商都等于1；②对于任何正整数n，（﹣1）_n＝﹣1；③3₄＝4₃；④负数的奇数次商结果是负数，负数的偶数次商结果是正数.

(3)、深入思考
我们知道，有理数的减法运算可以转化为加法运算，除法运算能够转化为乘法运算，那么有理数的除方运算如何转化为乘方运算呢？例：

2_{4} = 2 \div 2 \div 2 \div 2 = 2 \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = {(\frac{1}{2})}^{2}

.
试一试：仿照上面的算式，将下列运算结果直接写成乘方（幂）的形式（﹣3）₄＝；

{(\frac{1}{7})}_{5}

＝；

(4)、想一想：将一个非零有理数a的n次商写成幂的形式等于；

(5)、算一算：

5_{2} \div {(- \frac{1}{2})}_{4} \times {(- \frac{1}{3})}_{5} + {(- \frac{1}{4})}_{3} \times \frac{1}{4}

＝.

查看试题解析

12. 某集团公司对所属甲.乙两分厂下半年经营情况记录（其中“+”表示盈利，“﹣”表示亏损，单位：亿元）如下表.

月份	七月份	八月份	九月份	十月份	十一月份	十二月份
甲厂	-0.2	-0.4	+0.5	0	+1.2	+1.3
乙厂	+1.0	-0.7	-1.5	+1.8	-1.8	0

(1)、计算八月份乙厂比甲厂多亏损多少亿元？

(2)、分别计算下半年甲、乙两个工厂平均每月盈利或亏损多少亿元？

查看试题解析

13. 阅读下面解题过程：

计算： $(- 15) \div (\frac{1}{3} - \frac{3}{2} - 3) \times 6$

解：原式= $(- 15) \div (- \frac{25}{6}) \times 6$ （第①步）

= $(- 15) \div (- \frac{25}{6}) \times 6$ （第②步）

=(－15)÷(－25)（第③步）

= $- \frac{3}{5}$ （第④步）

(1)、上面解题过程中有错误的步骤是．（填序号）

(2)、请写出正确的解题过程．

查看试题解析

14. 列式计算：

(1)、一个数与

- \frac{3}{4}

的差为

\frac{1}{2}

，求这个数；

(2)、

- \frac{9}{4}

除以一个数的商为

- 9

，求这个数.

查看试题解析

15. 阅读下面题目解题过程：

计算： $(- 15) \div (\frac{1}{3} - \frac{1}{2}) \times 6$

$= (- 15) \div (- \frac{1}{6}) \times 6$ ①

$= (- 15) \div (- 1)$ ②

$= - 15$ ③

回答：

(1)、上面解题过程中有两个错误，第一处是，第二处是（填序号）；

(2)、改正：

查看试题解析

16. 如图，在数轴上点A表示数a，点B示数b，点C表示数c，b是最小的正整数，且a、c满足|a+2|+(c-6)²=0．

(1)、a= ， b= ， c=

(2)、若将数轴折叠，使得点A与点C重合，则数轴上折痕所表示的数为，点B与数出表示的点重合，原点与数表示的点重合．

(3)、动点P、Q同时从原点出发，点P向负半轴运动，点Q向正半轴运动，点Q的速度是点P速度的3倍，2秒钟后，点P到达点A．

①点P的速度是每秒 ▲ 个单位，则点Q的速度是每秒 ▲ 个单位．

②点Q到达点C后，改变方向，按原速度向负半轴方向运动．求再经过几秒钟，点P与点Q能相遇．

③在②的条件下，点Q改变方向后，直接写出又经过几秒钟点P与点Q相距3个单位.

查看试题解析

17. 已知10×10²＝1000＝10³ ，

10²×10²＝10000＝10⁴ ，

10²×10³＝100000＝10⁵.

(1)、猜想10⁶×10⁴＝， 10^m×10ⁿ＝.（m，n均为正整数）

(2)、运用上述猜想计算下列式子：

①（1.5×10⁴）×（1.2×10⁵）；

②（﹣6.4×10³）×（2×10⁶）.

查看试题解析

18. 2021年7月24日，东京奥运会十米气步枪决赛中，中国选手杨倩为中国代表队摘得首金，其中最后10枪的成绩如下表所示：

序号	①	②	③	④	⑤	⑥	⑦	⑧	⑨	⑩
环数	10.2	10.8	10.0	10.6	10.6	10.5	10.7	10.6	10.7	9.8

若以10.5环为基准，记录相对环数，超过的环数记为正数，不足的环数记为负数，则上述成绩可表示为：

序号	①	②	③	④	⑤	⑥	⑦	⑧	⑨	⑩
相对环数	-0.3	0.3	-0.5	0.1	0.1	0		0.1	0.2

(1)、请填写表中的两个空格：、

(2)、这10枪中，与10.5环偏差最大的那次射击的序号为；

(3)、请计算这10枪的总成绩。

查看试题解析

19. 某粮库1月7日到9日这3天内进出库的吨数记录如下（“+”表示进库，“﹣”表示出库）：

日期	1月7日	1月8日	1月9日
进出库情况	+26，﹣38	﹣20，+34	﹣32，﹣15

(1)、经过这3天进出库后，粮库管理员结算时发现粮库里结存480吨粮食，那么3天前粮库里的存量有多少吨？

(2)、如果进库出库的装卸费都是每吨10元，那么这3天要付出多少装卸费？

查看试题解析

20. 某市居民使用自来水按如下标准收费（水费按月缴纳）

居民月用水量	不超过10m³的部分	超过10m³但不超过18m³的部分	超过18m³的部分
单价	2元/m³	3元/m³	4元/m³

(1)、某用户一个月用了15m³水，求该用户这个月应缴纳的水费；

(2)、设某户月用水量为n立方米，当n＞18时，求该用户应缴纳的水费（用含n的代数式表示）；

(3)、甲、乙两用户一个月共用水36m³ ，已知甲用户缴纳的水费超过了20元．设甲用户这个月用水xm³ ，则甲、乙两用户一个月共缴纳的水费为多少元？（用含x的代数式表示）．

查看试题解析

21. 用激光技术测得地球和月球之间的距离为377985654.32米，请按要求分别取得这个数的近似值，并分别写出相应的有效数字.

(1)、精确到千位；

(2)、精确到千万位；

(3)、精确到亿位.

查看试题解析

22. 李先生在2019年10月第2周星期五股市收盘时，以每股9元的价格买进某公司的股票1000股，在11月第2周的星期一至星期五，该股票每天收盘时每股的涨跌（单位：元）情况如下表：

时间	星期一	星期二	星期三	星期四	星期五
每股涨跌/元	0	-0.32	+0.47	-0.21	+0.56

注：表中记录的数据为每天收盘价格与前一天收盘价格的变化量，星期一的数据是与上星期五收盘价格的变化量．

(1)、请你判断在11月的第2周内，该股票价格收盘时，价格最高的是哪一天？

(2)、在11月第2周内，求李先生购买的股票每股每天平均的收盘价格．（结果精确到百分位）

查看试题解析

23. 用四舍五入法按要求取近似数：

(1)、2367890(精确到十万位);

(2)、29524（精确到千位);

(3)、4.2046(精确到千分位)

(4)、3.102(精确到百分位).

查看试题解析

浙教版数学七上第2章 有理数的运算优生综合题特训

一、综合题

浙教版数学七上第2章有理数的运算优生综合题特训