山东省济南市长清区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-07 类型:期中考试
一、单选题
-
1. 方程 的解是( )A、 B、 C、 D、无实数根2. 如图所示,圆柱的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 不透明布袋中装有除颜色外完全相同的1个红球和2个白球,搅匀后从中摸出一个球是白球的概率是( )A、 B、 C、 D、4. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、5. a, b,c,d 是成比例线段,若 a = 3cm, b = 2cm,c = 6cm,则线段d的长为( )A、3cm B、4cm C、5cm D、6cm6. 如图所示,某校数学兴趣小组利用标杆BE测量物的高度,已知标杆BE高1.5m,测得AB=1.2m,AC=14m,则建筑物CD的高是( )
3. 不透明布袋中装有除颜色外完全相同的1个红球和2个白球,搅匀后从中摸出一个球是白球的概率是( )A、 B、 C、 D、4. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、5. a, b,c,d 是成比例线段,若 a = 3cm, b = 2cm,c = 6cm,则线段d的长为( )A、3cm B、4cm C、5cm D、6cm6. 如图所示,某校数学兴趣小组利用标杆BE测量物的高度,已知标杆BE高1.5m,测得AB=1.2m,AC=14m,则建筑物CD的高是( ) A、17.5m B、17m C、16.5m D、18m7. 关于x的一元二次方程(m﹣1)x2﹣2x﹣1=0有两个不相等的实数根,则实数m的取值范围是( )A、m>0且m≠1 B、m>0 C、m≥0且m≠1 D、m≥08. 在一个不透明的袋子里装有红球、黄球共 个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在 左右,则袋子中红球的个数最有可能是( )A、5 B、10 C、12 D、159. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( )
A、17.5m B、17m C、16.5m D、18m7. 关于x的一元二次方程(m﹣1)x2﹣2x﹣1=0有两个不相等的实数根,则实数m的取值范围是( )A、m>0且m≠1 B、m>0 C、m≥0且m≠1 D、m≥08. 在一个不透明的袋子里装有红球、黄球共 个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在 左右,则袋子中红球的个数最有可能是( )A、5 B、10 C、12 D、159. 如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程s之间的变化关系用图象刻画出来,大致图象是( ) A、
A、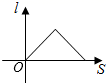 B、
B、 C、
C、 D、
D、 10. 在一次同学聚会上,参加的每个人都与其他人握手一次,共握手95次,设参加这次同学聚会的有x人,可得方程( )A、x(x﹣1)=190 B、x(x﹣1)=380 C、x(x﹣1)=95 D、(x﹣1)2=38011. 图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 ( )
10. 在一次同学聚会上,参加的每个人都与其他人握手一次,共握手95次,设参加这次同学聚会的有x人,可得方程( )A、x(x﹣1)=190 B、x(x﹣1)=380 C、x(x﹣1)=95 D、(x﹣1)2=38011. 图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面 ( )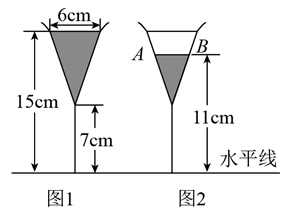 A、 B、 C、 D、12. 如图,在矩形ABCD中, , .将矩形ABCD对折,得到折痕MN后展开;连接MC,将 沿CM折叠,点D的对应点为E,ME与BC的交点为F;P是线段BN上一点,连接MP,将四边形AMPB沿MP折叠,点B的对应点为G,当AM与EM重合时FE的长是( )
A、 B、 C、 D、12. 如图,在矩形ABCD中, , .将矩形ABCD对折,得到折痕MN后展开;连接MC,将 沿CM折叠,点D的对应点为E,ME与BC的交点为F;P是线段BN上一点,连接MP,将四边形AMPB沿MP折叠,点B的对应点为G,当AM与EM重合时FE的长是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知4a=3b,则 = .14. 如图所示,转盘被分成面积相等的8份,小强随机转动转盘一次,则指针指到偶数的概率是 .
 15. 已知关于x的一元二次方程x2﹣mx+6=0.其中一个解x=3,则m的值为 .16. 某一时刻,身高1.6m的小明在阳光下的影长是0.6m,同一时刻同一地点测得旗杆的影长是3m,则该旗杆的高度是 m.17. 如图,在一幅长80cm,宽50cm的长方形风景画的四周镶上一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是5400cm2 , 则金色纸边的宽为cm.
15. 已知关于x的一元二次方程x2﹣mx+6=0.其中一个解x=3,则m的值为 .16. 某一时刻,身高1.6m的小明在阳光下的影长是0.6m,同一时刻同一地点测得旗杆的影长是3m,则该旗杆的高度是 m.17. 如图,在一幅长80cm,宽50cm的长方形风景画的四周镶上一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是5400cm2 , 则金色纸边的宽为cm. 18. 如图,四边形ABCD是正方形,AB=6,E是BC中点,连接DE,DE的垂直平分线分别交AB、DE、CD于M、O、N,连接EN,过E作EF⊥EN交AB于F.下列结论中,正确结论是 . (填序号)
18. 如图,四边形ABCD是正方形,AB=6,E是BC中点,连接DE,DE的垂直平分线分别交AB、DE、CD于M、O、N,连接EN,过E作EF⊥EN交AB于F.下列结论中,正确结论是 . (填序号)①△BEF∽△CNE;②MN=3 ;③BF= AF;④△BEF的周长是12.

三、解答题
-
19. 解方程:x2﹣4x=3.20. 如图,l1∥l2∥l3 , AB=5,DE=4,EF=8,求AC的长.
 21. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示.
21. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示.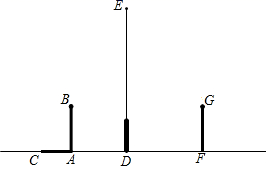 (1)、请你通过画图确定灯泡所在的位置.(2)、如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.22. 已知:如图,在正方形ABCD中,P是BC上的点,Q是CD上的点,且AQ⊥PQ,△ADQ与△QCP是否相似?并证明你的结论.
(1)、请你通过画图确定灯泡所在的位置.(2)、如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.22. 已知:如图,在正方形ABCD中,P是BC上的点,Q是CD上的点,且AQ⊥PQ,△ADQ与△QCP是否相似?并证明你的结论. 23. 如图,O为原点,B,C两点坐标分别为(3,−1) ,(2,1).
23. 如图,O为原点,B,C两点坐标分别为(3,−1) ,(2,1). (1)、以O为位似中心在y轴左侧将ΔOBC放大两倍,并画出图形;(2)、分别写出B,C两点的对应点B′,C′的坐标;(3)、已知M(x,y)为ΔOBC内部一点,写出M的对应点M′的坐标.24. 汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2016年盈利1500万元,到2018年盈利2160万元,且从2016年到2018年,每年盈利的年增长率相同.(1)、求每年盈利的年增长率;(2)、若该公司盈利的年增长率继续保持不变,那么2019年该公司盈利能否达到2500万元?25. 2019年12月以来,湖北省武汉市部分医院陆续发现不明原因肺炎病例,现已证实该肺炎为一种新型冠状病毒感染的肺炎,其传染性较强.为了有效地避免交叉感染,需要采取以下防护措施:①戴口罩;②勤洗手;③少出门;④重隔离;⑤捂口鼻;⑥谨慎吃.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.
(1)、以O为位似中心在y轴左侧将ΔOBC放大两倍,并画出图形;(2)、分别写出B,C两点的对应点B′,C′的坐标;(3)、已知M(x,y)为ΔOBC内部一点,写出M的对应点M′的坐标.24. 汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2016年盈利1500万元,到2018年盈利2160万元,且从2016年到2018年,每年盈利的年增长率相同.(1)、求每年盈利的年增长率;(2)、若该公司盈利的年增长率继续保持不变,那么2019年该公司盈利能否达到2500万元?25. 2019年12月以来,湖北省武汉市部分医院陆续发现不明原因肺炎病例,现已证实该肺炎为一种新型冠状病毒感染的肺炎,其传染性较强.为了有效地避免交叉感染,需要采取以下防护措施:①戴口罩;②勤洗手;③少出门;④重隔离;⑤捂口鼻;⑥谨慎吃.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.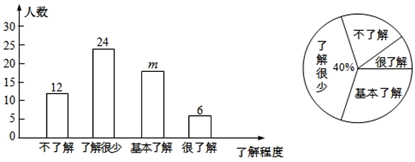
请你根据上面的信息,解答下列问题
(1)、本次共调查了名员工,条形统计图中 ;(2)、若该公司共有员工1000名,请你估计不了解防护措施的人数;(3)、在调查中,发现有4名员工对防护措施很了解,其中有3名男员工、1名女员工.若准备从他们中随机抽取2名,让其在公司群内普及防护措施,求恰好抽中一男一女的概率.26. 如图,在Rt△ABC中,AC=4cm,BC=3cm,点P由点B出发沿BA的方向向点A匀速运动,速度为1cm/s,同时点Q由A出发沿AC方向向点C匀速运动,速度为1cm/s,连接PQ.设运动的时间为t(s),其中0<t<4.解答下列问题: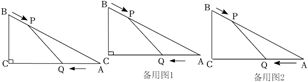 (1)、AP= , AQ=;(用含t的代数式麦示)(2)、当t为何值时,以P、Q、A为顶点的三角形与△ABC相似?(3)、点P、Q在运动过程中,△APQ能否成为等腰三角形?若能,求出此时t的值;若不存在,请说明理由.27. 如图
(1)、AP= , AQ=;(用含t的代数式麦示)(2)、当t为何值时,以P、Q、A为顶点的三角形与△ABC相似?(3)、点P、Q在运动过程中,△APQ能否成为等腰三角形?若能,求出此时t的值;若不存在,请说明理由.27. 如图 (1)、(问题发现)如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为;(2)、(拓展研究)在(1)的条件下,如果正方形CDEF绕点C旋转,当点B,E,F三点共线时,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;(3)、(问题发现)当正方形CDEF旋转到B,E,F三点共线时,求线段AF的长.
(1)、(问题发现)如图1,在Rt△ABC中,AB=AC=4,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为;(2)、(拓展研究)在(1)的条件下,如果正方形CDEF绕点C旋转,当点B,E,F三点共线时,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;(3)、(问题发现)当正方形CDEF旋转到B,E,F三点共线时,求线段AF的长.