山东省滨州市无棣县2021-2022学年九年级上学期期中考试数学试题
试卷更新日期:2021-12-07 类型:期中考试
一、单选题
-
1. 下列图形中,是中心对称图形但不是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 用公式法解一元二次方程 时,化方程为一般式,当中的a,b,c依次为( )A、3,﹣4,8 B、3,﹣4,﹣8 C、3,4﹣8 D、3,4,83. 抛物线 的顶点坐标是( )A、 B、 C、 D、4. 若函数 是关于x的二次函数,则m的值是( )A、2 B、-1或3 C、3 D、5. 点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )A、40° B、100° C、40°或140° D、40°或100°6. 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A按逆时针方向旋转到△AB'C'的位置,使得CC′∥AB,则∠BAB′=( )
2. 用公式法解一元二次方程 时,化方程为一般式,当中的a,b,c依次为( )A、3,﹣4,8 B、3,﹣4,﹣8 C、3,4﹣8 D、3,4,83. 抛物线 的顶点坐标是( )A、 B、 C、 D、4. 若函数 是关于x的二次函数,则m的值是( )A、2 B、-1或3 C、3 D、5. 点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )A、40° B、100° C、40°或140° D、40°或100°6. 如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A按逆时针方向旋转到△AB'C'的位置,使得CC′∥AB,则∠BAB′=( ) A、30° B、35° C、40° D、50°7. 若关于x的一元二次方程 有实数根,则实数k的取值范围是( )A、 B、 C、 且 D、8. 如图,PA,PB分别与⊙O相切于A,B两点,若∠C=65°,则∠P的度数为( )
A、30° B、35° C、40° D、50°7. 若关于x的一元二次方程 有实数根,则实数k的取值范围是( )A、 B、 C、 且 D、8. 如图,PA,PB分别与⊙O相切于A,B两点,若∠C=65°,则∠P的度数为( ) A、65° B、130° C、50° D、100°9. 如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧 的长等于( )
A、65° B、130° C、50° D、100°9. 如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧 的长等于( ) A、 B、 C、 D、10. 关于x的一元二次方程 的一个根为0,则实数a的值为( )A、-1 B、0 C、1 D、-1或111. 如图,已知抛物线 与 轴分别交于 、 两点,将抛物线 向上平移得到 ,过点 作 轴交抛物线 于点 ,如果由抛物线 、 、直线 及 轴所围成的阴影部分的面积为 ,则抛物线 的函数表达式为( )
A、 B、 C、 D、10. 关于x的一元二次方程 的一个根为0,则实数a的值为( )A、-1 B、0 C、1 D、-1或111. 如图,已知抛物线 与 轴分别交于 、 两点,将抛物线 向上平移得到 ,过点 作 轴交抛物线 于点 ,如果由抛物线 、 、直线 及 轴所围成的阴影部分的面积为 ,则抛物线 的函数表达式为( ) A、 B、 C、 D、12. 已知抛物线y= x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( ,3),P是抛物线y= x2+1上一个动点,则△PMF周长的最小值是( )
A、 B、 C、 D、12. 已知抛物线y= x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( ,3),P是抛物线y= x2+1上一个动点,则△PMF周长的最小值是( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
13. 菱形ABCD的一条对角线长为6,边AB的长是方程 的一个根,则菱形ABCD的周长为14. 新冠病毒传染性很强,如不注重个人防疫,有一个人感染,经过两轮传染后共有144人会被感染.若设平均每轮传染x人,则可列方程为 .15. 已知抛物线y=x2+mx+9的顶点在x轴上,则m的值为.16. 如图,已知圆O为 的内切圆,切点分别为D、E、F,且 , , ,则圆O的半径为 .
 17. 已知二次函数y=x2+2mx+2,当x>2时,y的值随x值的增大而增大,则实数m的取值范围是 .18. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
17. 已知二次函数y=x2+2mx+2,当x>2时,y的值随x值的增大而增大,则实数m的取值范围是 .18. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0. 其中,正确的结论有 .

三、解答题
-
19. 小敏与小霞两位同学解方程 的过程如下框:
小敏:
两边同除以 ,得
,
则 .
小霞:
移项,得 ,
提取公因式,得 .
则 或 ,
解得 , .
你认为他们的解法是否正确?若正确请在框内打“√”;若不正确请在框内打“×”,并写出你的解答过程.
20. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.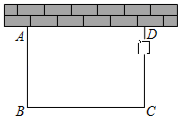 21. 如图,在 中, , 于点 , 于点 .
21. 如图,在 中, , 于点 , 于点 .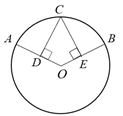 (1)、求证: ;(2)、若 , ,求四边形 的面积.22. 为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价 (单位:万元)成一次函数关系.
(1)、求证: ;(2)、若 , ,求四边形 的面积.22. 为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价 (单位:万元)成一次函数关系.
(1)、求年销售量 与销售单价 的函数关系式;(2)、根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?23. 如图, 与等边 的边 , 分别交于点 , , 是直径,过点 作 于点 .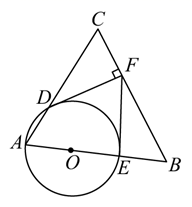 (1)、求证: 是 的切线;(2)、连接 ,当 是 的切线时,求 的半径 与等边 的边长 之间的数量关系.24. 如图,已知抛物线 与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC.
(1)、求证: 是 的切线;(2)、连接 ,当 是 的切线时,求 的半径 与等边 的边长 之间的数量关系.24. 如图,已知抛物线 与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC. (1)、求A、B、C三点的坐标;(2)、若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当线段PM的长度最大时,求点M的坐标;(3)、在(2)的条件下,当线段PM的长度最大时,在抛物线的对称轴上有一点Q,使得△CNQ为直角三角形,直接写出点Q的坐标.
(1)、求A、B、C三点的坐标;(2)、若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当线段PM的长度最大时,求点M的坐标;(3)、在(2)的条件下,当线段PM的长度最大时,在抛物线的对称轴上有一点Q,使得△CNQ为直角三角形,直接写出点Q的坐标.