辽宁省营口市鲅鱼圈区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-12-07 类型：期中考试

进入出卷网下载

一、单选题

1. 下面几种中式窗户图形既是轴对称又是中心对称的是（）

A、 B、 C、 D、

查看试题解析
2. 若关于x的一元二次方程kx²+2x–1=0有实数根，则实数k的取值范围是

A、k≥–1 B、k>–1 C、k≥–1且k≠0 D、k>–1且k≠0

查看试题解析
3. 如图，BC是 $⊙ O$ 的直径，A，D是 $⊙ O$ 上的两点，连接AB，AD，BD，若 $∠ A D B = 70^{°}$ ，则 $∠ A B C$ 的度数是（）

A、20° B、70° C、30° D、90°

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $2 \sqrt{3} - \sqrt{3} = 2$ C、 $2 \sqrt{3} \times 3 \sqrt{3} = 6 \sqrt{3}$ D、 $\sqrt{6} \div \sqrt{2} = \sqrt{3}$

查看试题解析
5. 如图，矩形 $A B C D$ 的对角线交于点 $O$ ，若 $∠ A C B = 30 °$ ， $A B = 2$ ，则 $O C$ 的长为（）

A、2 B、3 C、 $2 \sqrt{3}$ D、4

查看试题解析
6. 为了解某市参加中考的25000名学生的身高情况，抽查了其中1200名学生的身高进行统计分析.下列叙述正确的是（）

A、25000名学生是总体 B、1200名学生的身高是总体的一个样本 C、每名学生是总体的一个个体 D、以上调查是全面调查

查看试题解析
7. 如图， $P A$ 、 $P B$ 为⊙O的切线，切点分别为A、B， $P O$ 交 $A B$ 于点C， $P O$ 的延长线交⊙O于点D．下列结论不一定成立的是（）

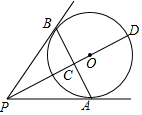A、 $△ B P A$ 为等腰三角形 B、 $A B$ 与 $P D$ 相互垂直平分 C、点A，B都在以 $P O$ 为直径的圆上 D、 $P C$ 为 $△ B P A$ 的边 $A B$ 上的中线

查看试题解析
8. 已知一次函数y=（a+1）x+b的图象如图所示，那么a的取值范围是（）

A、 $a > 1$ B、 $a < - 1$ C、 $a > - 1$ D、 $a < 0$

查看试题解析
9. 如图，等腰直角三角形ABC的直角顶点C与平面直角坐标系的坐标原点O重合，AC，BC分别在坐标轴上，AC=BC=1，△ABC在x轴正半轴上沿顺时针方向作无滑动的滚动，在滚动过程中，当点C第一次落在x轴正半轴上时，点A的对应点A₁的横坐标是（）

A、2 B、3 C、1+ $\sqrt{2}$ D、2+ $\sqrt{2}$

查看试题解析
10. 如图，二次函数y=ax²+bx+c(a≠0)的图象与x轴交于A、B两点，与y轴交于点C，对称轴是直线x=-1，点B的坐标为(1，0)．下面的四个结论：①AB=4；②b²-4ac>0；③ab<0；④a-b+c<0，其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 在网络上搜索“奔跑吧,兄弟”,能搜索到与之相关的结果为35 800 000个,将35 800 000用科学记数法表示为 .

查看试题解析
12. 已知一组数据：18，17，13，15，17，16，14，17，则这组数据的中位数与众数分别是．

查看试题解析
13. 若分式 $\frac{2 a + 3}{a - 1}$ 有意义，则a的取值范围是．

查看试题解析
14. 某市为绿化环境计划植树2400棵，实际劳动中每天植树的数量比原计划多20%，结果提前8天完成任务．若设原计划每天植树x棵，则根据题意可列方程为．

查看试题解析
15. 如图，在△ABC 中，AC＝BC，∠ACB＝90°，点 D 在 BC 上，BD＝3，DC＝1，点 P 是 AB 上的动点，则 PC+PD 的最小值为

查看试题解析
16. 如图，在矩形ABCD中，AD＝8，AB＝4，将矩形ABCD折叠，使点A与点C重合，折痕为MN．给出以下四个结论：①△CDM≌△CEN；②△CMN是等边三角形；③CM＝5；④BN＝3．其中正确的结论序号是．

查看试题解析

三、解答题

17. 解方程：

(1)、 $(x - 3) (x - 1) = 3$ ．

(2)、 $3 x^{2} - 2 x - 2 = 0$ ．

查看试题解析
18. 先化简，再求值： $\frac{x - 3}{x^{2} - 4} \div (x + 2 - \frac{x^{2} - 2 x + 2}{x - 2})$ ，其中 $x = \sqrt{5} - 2^{- 1} - \frac{3}{2}$ ．

查看试题解析
19. 学校为了了解全校1600名学生对“初中学生带手机上学”现象的看法，在全校随机抽取了若干名学生进行问卷调查．问卷给出了四种看法供学生选择，每人只能选一种，且不能不选．将调查结果整理后，绘制成如图①、图②所示的条形统计图与扇形统计图(均不完整)．

(1)、在这次调查中，一共抽取了多少名学生？

(2)、补全条形统计图和扇形统计图；

(3)、估计全校有多少名学生对“初中学生带手机上学”现象持“不赞同”的看法．

查看试题解析
20. 防疫期间，某公司购买 $A 、 B$ 两种不同品牌的免洗洗手液，若购买A种10件， $B$ 种5件，共需130元；若购A种5件， $B$ 种10件，共需140元．

(1)、 $A 、 B$ 两种洗手液每件各多少元？

(2)、若购买 $A 、 B$ 两种洗手液共100件，且总费用不超过900元，则A种洗手液至少需要购买多少件？

查看试题解析
21. $△ A B C$ 与 $△ C D E$ 都是等边三角形，连接AD、BE．

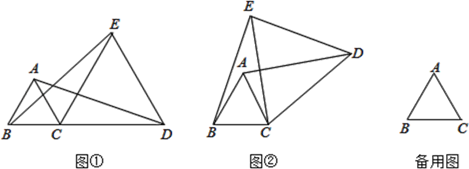(1)、如图①，当点B、C、D在同一条直线上时，则 $∠ B C E =$ 度；

(2)、将图①中的 $△ C D E$ 绕着点C逆时针旋转到如图②的位置，求证： $A D = B E$ ．

查看试题解析
22. 某经销商销售一种产品，这种产品的成本价为10元/件，规定销售价不低于成本价，且不高于35元，市场调查发现，该产品每天的销售量 $y$ （件）与销售价 $x$ （元/件）满足一次函数关系，如图所示．

(1)、求 $y$ 与 $x$ 之间的函数关系式；

(2)、若经销商想要每天获得550元的利润，销售价应该定为多少？

(3)、设每天的销售利润为 $w$ （元），当销售价为多少元时，每天获得的利润最大，最大利润是多少？

查看试题解析
23. 如图，△ABD是⊙O的内接三角形，E是弦BD的中点，点C是⊙O外一点，且∠DBC＝∠A＝60°，连接OE并延长与⊙O相交于点F，与BC相交于点C．

(1)、求证：BC是⊙O的切线；

(2)、若⊙O的半径为6cm，求弦BD的长．

查看试题解析
24. 在等腰Rt△ABC中，AB＝AC，∠BAC＝90°

(1)、如图1，D，E是等腰Rt△ABC斜边BC上两动点，且∠DAE＝45°，将△ABE绕点A逆时针旋转90后，得到△AFC，连接DF
①求证：△AED≌△AFD；

②当BE＝3，CE＝7时，求DE的长；

(2)、如图2，点D是等腰Rt△ABC斜边BC所在直线上的一动点，连接AD，以点A为直角顶点作等腰Rt△ADE，当BD＝3，BC＝9时，求DE的长．

查看试题解析
25. 已知抛物线 $y = a x^{2} + b x + 8 (a \neq 0)$ 经过点A(-3，-7)，B(3，5)，顶点为点E，抛物线的对称轴与直线AB交于点C．

(1)、求直线AB的解析式和抛物线的解析式．

(2)、在抛物线上A，E两点之间的部分(不包含A，E两点)，是否存在点D，使得 $S_{△ D A C} = 2 S_{△ D C E}$ ？若存在，求出点D的坐标；若不存在，请说明理由．

(3)、若点P在抛物线上，点Q在x轴上，当以点A，E，P，Q为顶点的四边形是平行四边形时，直接写出满足条件的点P的坐标．

查看试题解析