辽宁省朝阳市2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-07 类型:期中考试
一、单选题
-
1. 在下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 关于 一元二次方程 的一个根是0,则 的值为( )A、1或-1 B、1 C、-1 D、03. 设A( , ),B( , ),C(3, )是抛物线 上的三点,则 , , 的大小关系为( )A、 B、 C、 D、4. 方程 的根的情况是( )A、只有一个实数根 B、没有实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 二次函数 的图象的开口方向,对称轴和顶点坐标为( )A、开口向上,对称轴为直线 ,顶点 B、开口向上,对称轴为直线 ,顶点(1,5) C、开口向下,对称轴为直线 ,顶点(1, ) D、开口向上,对称轴为直线 ,顶点(1, )6. 如图, 中, , cm, cm,动点 从点 出发沿 边以 cm /秒的速度向点 移动,点 从点 出发,沿 边以 cm /秒的速度向点 移动,如果点 , 分别从点 , 同时出发,在运动过程中,设点 的运动时间为 ,则当 的面积为 cm2时, 的值( )
2. 关于 一元二次方程 的一个根是0,则 的值为( )A、1或-1 B、1 C、-1 D、03. 设A( , ),B( , ),C(3, )是抛物线 上的三点,则 , , 的大小关系为( )A、 B、 C、 D、4. 方程 的根的情况是( )A、只有一个实数根 B、没有实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 二次函数 的图象的开口方向,对称轴和顶点坐标为( )A、开口向上,对称轴为直线 ,顶点 B、开口向上,对称轴为直线 ,顶点(1,5) C、开口向下,对称轴为直线 ,顶点(1, ) D、开口向上,对称轴为直线 ,顶点(1, )6. 如图, 中, , cm, cm,动点 从点 出发沿 边以 cm /秒的速度向点 移动,点 从点 出发,沿 边以 cm /秒的速度向点 移动,如果点 , 分别从点 , 同时出发,在运动过程中,设点 的运动时间为 ,则当 的面积为 cm2时, 的值( ) A、2或3 B、2或4 C、1或3 D、1或47. 如图,抛物线 与 轴交于点 ,其对称轴为直线 ,结合图象分析下列结论:① ;② ;③当 时, 随 的增大而增大;④一元二次方程 的两根分别为 , ;⑤若 为方程 的两个根,则 且 ,其中正确的结论有( )个.
A、2或3 B、2或4 C、1或3 D、1或47. 如图,抛物线 与 轴交于点 ,其对称轴为直线 ,结合图象分析下列结论:① ;② ;③当 时, 随 的增大而增大;④一元二次方程 的两根分别为 , ;⑤若 为方程 的两个根,则 且 ,其中正确的结论有( )个. A、2 B、3 C、4 D、58. 如图,在 中, , , .点P是 边上的一个动点,过点P作 交直角边于点D,设 为x, 的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A、2 B、3 C、4 D、58. 如图,在 中, , , .点P是 边上的一个动点,过点P作 交直角边于点D,设 为x, 的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、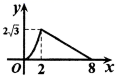 D、
D、 9. 二次函数 的大致图象如图所示,关于该二次函数,下列说法错误的是( )
9. 二次函数 的大致图象如图所示,关于该二次函数,下列说法错误的是( ) A、函数有最小值 B、对称轴是直线 C、当 时,y随x的增大而减小 D、当 时,10. 在平面直角坐标系中,一个蜘蛛最初在点 ( 是常数,且 ),第一次爬到射线 绕 点逆时针旋转 方向上的 点,且 ;第二次爬到射线 绕 点逆时针旋转 方向上的 点,且 ;…;第 次爬行到 点的坐标是( )
A、函数有最小值 B、对称轴是直线 C、当 时,y随x的增大而减小 D、当 时,10. 在平面直角坐标系中,一个蜘蛛最初在点 ( 是常数,且 ),第一次爬到射线 绕 点逆时针旋转 方向上的 点,且 ;第二次爬到射线 绕 点逆时针旋转 方向上的 点,且 ;…;第 次爬行到 点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在平面直角坐标系中,点P(﹣3,1)关于坐标原点中心对称的点P′的坐标是.12. 一元二次方程x2﹣x=0的根是 .13. 若 是关于x的一元二次方程,则m的取值范围是.14. 将抛物线 先向左平移1个单位后所得到的新抛物线的解析式为 .15. 如图,已知线段 的长为 ,以 为边在 的下方作正方形 .取 边上一点 ,以 为边在 的上方作正方形 .过 作 丄 ,垂足为 点.若正方形 与四边形 的面积相等,则 的长为 .
 16. 退休的李老师借助自家15米的院墙和总长度为30米的围栏,在院墙外设计一个矩形花圃种植花草.为方便进出,他在如图所示的位置安装了一个1米宽的门,如果设和墙相邻的一边长为x米,花圃面积为y平方米,则y与x之间的函数关系式为 .
16. 退休的李老师借助自家15米的院墙和总长度为30米的围栏,在院墙外设计一个矩形花圃种植花草.为方便进出,他在如图所示的位置安装了一个1米宽的门,如果设和墙相邻的一边长为x米,花圃面积为y平方米,则y与x之间的函数关系式为 .
三、解答题
-
17. 解方程: .18. 如图,矩形绿地的长、宽各增加 ,写出扩充后的绿地的面积y与x的关系式.
 19. 在如图所示的网格中按要求画出图形,并回答问题:
19. 在如图所示的网格中按要求画出图形,并回答问题:
⑴画出 以点O为旋转中心顺时针旋转 后的 ;
⑵画出 关于点O的中心对称图形 .
20. 对于实数u、v,定义一种运算“*”为: .若关于x的方程 有两个相等的实数根,求满足条件的实数a的值.21. 已知二次函数y=(m2﹣2)x2﹣4mx+n的图象的对称轴是直线x=2,且最高点在直线y= x+1上,求这个二次函数的表达式.22. 某种病毒传播非常快,如果一个人被感染,经过两轮感染后就会有121个人被感染.(1)、每轮感染中平均一个人会感染几个人?(2)、若病毒得不到有效控制,3轮感染后,被感染的人会不会超过1300人?23. 某宾馆有50间相同的客房,当房间的定价为每天180元时,房间会全部住满.统计表明:当房价每上调10元时,就会有一个房间空闲,宾馆需对有客人居住的房间每天支出20元的各种费用.设该宾馆房价上调x元(x为10的正整数倍)时,相应的住房数为y间.(1)、求y与x的函数关系式.(2)、房价为多少时,宾馆的利润最大?最大利润是多少?(3)、若老板决定每住进去一间房就捐出a元(0<a≤40)给当地福利院,同时要保证房间定价在180元至360元之间波动时(包括两端点),利润随x的增大而增大,求a的取值范围.24. 中, , , ,点 从点 开始沿边 向终点 以 的速度移动,与此同时,点 从点 开始沿边 向终点 以 的速度移动.如果 、 分别从 、 同时出发,当点 运动到点 时,两点停止运动.设运动时间为 秒. (1)、填空: , (用含 的代数式表示);(2)、当 为何值时, 的长度等于 ?(3)、是否存在 的值,使得 的面积等于 ?若存在,请求出此时 的值;若不存在,请说明理由.25. 如图,已知二次函数 的图象经过点 ,且对称轴是直线 .该函数图象和x轴交于B,C两点(点B在点C的左侧).
(1)、填空: , (用含 的代数式表示);(2)、当 为何值时, 的长度等于 ?(3)、是否存在 的值,使得 的面积等于 ?若存在,请求出此时 的值;若不存在,请说明理由.25. 如图,已知二次函数 的图象经过点 ,且对称轴是直线 .该函数图象和x轴交于B,C两点(点B在点C的左侧). (1)、求该函数解析式;(2)、求B,C两点的坐标;(3)、点P是直线AC下方抛物线上的一个动点,过点P作 ,垂足为Q,求PQ的最大值.
(1)、求该函数解析式;(2)、求B,C两点的坐标;(3)、点P是直线AC下方抛物线上的一个动点,过点P作 ,垂足为Q,求PQ的最大值.