辽宁省本溪市2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-12-07 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各组数中，互为倒数的是（）

A、-3和 $\frac{1}{3}$ B、2和-2 C、 $\sqrt{3}$ 和 $\frac{\sqrt{3}}{3}$ D、 $| - \sqrt{2} |$ 和 $\sqrt{2}$

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $a^{3} + 2 a^{3} = 3 a^{3}$ C、 $m^{2} \cdot m^{3} = m^{6}$ D、 ${(- 2 a^{3})}^{2} = - 4 a^{6}$

查看试题解析
3. 下列图形，是轴对称图形但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图所示的几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 下列说法中错误的是（）

A、两条对角线互相垂直且平分的四边形是菱形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直、平分且相等的四边形是正方形 D、两条对角线互相平分的四边形是平行四边形

查看试题解析
6. 一个不透明的袋子里装有黄球18个和红球若干，小明通过多次摸球试验后发现摸到红球的频率稳定在0.4左右，则袋子里有红球（）个

A、12 B、15 C、18 D、24

查看试题解析
7. 如图，在 $△ A B C$ 中点A的坐标为 $(3 ， 6)$ ，以原点O为位似中心，将 $△ A B C$ 位似缩小后得到 $△ A^{'} B^{'} C^{'}$ ．若点 $A^{'}$ 的坐标为 $(1 ， 2)$ ， $△ A^{'} B^{'} C^{'}$ 的面积为1，则 $△ A B C$ 的面积为（）

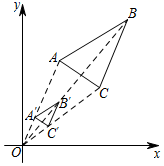A、3 B、6 C、9 D、12

查看试题解析
8. 如图，在菱形ABCD中， $A B = 4$ ， $∠ B A D = 120 °$ ， $△ A E F$ 为等边三角形点E，F分别在菱形的边BC，CD上滑动，且E，F不与B，C，D重合，则四边形AECF的面积是（）

A、4 B、 $4 \sqrt{3}$ C、8 D、 $8 \sqrt{3}$

查看试题解析
9. 如图，有一块锐角三角形材料，边 $B C = 60 mm$ ，高 $A D = 45 mm$ ，要把它加工成矩形零件，使其边在BC上，其余两个顶点分别在AB，AC上，且 $E H = 2 E F$ ，则这个矩形零件的长为（）

A、32mm B、36mm C、40mm D、44mm

查看试题解析
10. 如图1，四边形ABCD中， $A B / / C D$ ， $∠ B = 90 °$ ， $A C = A D$ ．动点Р从点B出发，沿折线 $B - A - D - C$ 方向以 $a$ 单位/秒的速度匀速运动，在整个运动过程中， $△ B C P$ 的面积S与运动时间t（秒）的函数图象如图2所示，则四边形ABCD的面积是（）

A、75 B、80 C、85 D、90

查看试题解析

二、填空题

11. 某红外线波长为0.00000094米，数字0.00000094用科学记数法表示为．

查看试题解析
12. 分解因式： $3 a^{3} - 27 a b^{2} =$ .

查看试题解析
13. 如果关于 $x$ 的一元二次方程 $(m - 2) x^{2} + 2 x + 1 = 0$ 有两个不相等的实数根，那么 $m$ 的取值范围为.

查看试题解析
14. 在一次中学生田径运动会上，参加男子跳高的14名运动员成绩如下表所示：

成绩/m

1.50

1.61

1.66

1.70

1.75

1.78

人数

2

3

2

1

5

1

则这些运动员成绩的中位数是.

查看试题解析
15. 如图，一飞镖游戏板由大小相等的小正方形格子构成，向游戏板随机投掷一枚飞镖，击中黑色区域的概率是．

查看试题解析
16. 如图所示，在Rt $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 6$ ，CM是斜边AB上的中线，E、F分别为MB、BC的中点，若 $E F = 2.5$ ，则 $△ E B F$ 的面积为．

查看试题解析
17. 在矩形ABCD中， $A B = 5$ ， $B C = 12$ ．点P在矩形ABCD的对角线BD上，点E在边BC上，满足 $△ P B E ∽ △ D B C$ ，若 $△ A P D$ 是等腰三角形，则PE的长为．

查看试题解析
18. 如图，点P是边长为2的正方形ABCD的对角线BD上的动点，过点P分别作 $P E ⊥ B C$ 于点E， $P F ⊥ D C$ 于点F，连接AP并延长，交射线BC于点H，交射线DC于点M，连接EF交AH于点G，当点P在BD上运动时（不包括B、D两点），以下结论：① $A H ⊥ E F$ ；② $M F = M C$ ；③ $E F^{2} = P M \cdot P H$ ；④EF的最小值是 $\sqrt{2}$ ．其中正确的是．（把你认为正确结论的序号都填上）

查看试题解析

三、解答题

19. 先化简，再求值： $(\frac{3}{a + 1} - a + 1) \div \frac{a^{2} - 4 a + 4}{a + 1}$ ，其中 $a$ 是4的平方根．

查看试题解析
20. 学完统计知识后，小明对同学们最近一周的睡眠情况进行随机抽样调查，得到他们每日平均睡眠时长 $t$ （单位：小时）的一组数据，将所得数据分为四组（A： $t < 8$ ；B： $8 \leq t < 9$ ；C： $9 \leq t < 10$ ；D： $t \geq 10$ ），并绘制成如下两幅不完整的统计图．

根据以上信息，解答下列问题：

(1)、小明一共抽样调查了名同学；在扇形统计图中，表示D组的扇形圆心角的度数为；

(2)、将条形统计图补充完整；

(3)、小明所在学校共有I400名学生，估计该校最近一周大约有多少名学生睡眠时长不足8小时?

(4)、A组的四名学生是2名男生和2名女生，若从他们中任选2人了解最近一周睡眠时长不足8小时的原因，试求恰好选中1名男生和I名女生的概率．

查看试题解析
21. 茶为国饮，茶文化是中国传统文化的重要组成部分，这也带动了茶艺、茶具、茶服等相关文化的延伸及产业的发展，在“春季茶叶节”期间，某茶具店老板购进了A、B两种不同的茶具．若购进A种茶具1套和B种茶具2套，需要250元：若购进A种茶具3套和B种茶具4套需要600元．

(1)、A、B两种茶具每套进价分别为多少元？

(2)、由于茶具畅销，茶具店老板决定再次购进A、B两种茶具共80套茶具厂对这两种类型的茶具进行了价格调整，A种茶具的进价比第一次购进时提高了8%，B种茶具的进价按第一次购进时进价的八折．如果茶具店老板此次用于购进A、B两种茶具的总费用不超过6240元，则茶具店老板最多能购进A种茶具多少套？

查看试题解析
22. 在 $▱ A B C D$ 中，AE平分 $∠ B A D$ ，交BC于点E，BF平分 $∠ A B C$ ，交AD于点F，AE与BF交于点O，连接EF、OC．

(1)、求证：四边形ABEF是菱形；

(2)、若点E为BC的中点，且 $B C = 8$ ， $∠ A B C = 60 °$ ，求OC的长．

查看试题解析
23. 九年级活动小组计划利用所学的知识测量操场旗杆高度.测量方案如下：如图，小卓在小越和旗杆之间的直线BM上平放一平面镜，在镜面上做了一个标记，这个标记在直线BM上的对应位置为点C，镜子不动，小卓看着镜面上的标记，他来回走动，走到点D时看到旗杆顶端点A在镜面中的像与镜面上的标记点C重合，这时测得小卓眼睛与地面的高度ED＝1.5米，CD＝1米，然后在阳光下，小越从D点沿DM方向走了15.8米到达F处此时旗杆的影子顶端与小越的影子顶端恰好重合，测得FG＝1.6米，FH＝3.2米，已知AB⊥BM，ED⊥BM，GF⊥BM若测量时所使用的平面镜的厚度忽略不计，请你根据图中提供的相关信息求出旗杆的高AB.

查看试题解析
24. 某环保公司研发了甲、乙两种智能设备，可将垃圾处理变为新型清洁燃料．某垃圾处理厂从环保公司购入以上两种智能设备若干，已知购买甲型智能设备花费360万元，购买乙型智能设备花费480万元，购买的两种设备数量相同，且两种智能设备的单价和为140万元．

(1)、求甲、乙两种智能设备单价；

(2)、垃圾处理厂利用智能设备生产燃料棒，并将产品出售．已知每吨燃料棒的成本为100元．调查发现，若燃料棒售价为每吨200元，平均每天可售出350吨，而当销售价每降低1元，平均每天可多售出5吨．垃圾处理厂想使这种燃料棒的销售利润平均每天达到36080元，且保证售价在每吨200元基础上降价幅度不超过8%，求每吨燃料棒售价应为多少元？

查看试题解析
25. 在 $△ A B C$ 中， $B A = B C$ ， $∠ A B C = α (0 ° < α < 180 °)$ ，点P为直线BC上一动点（不与点B、C重合），连接AP，将线段AP所在的直线绕点P顺时针旋转 $α$ 得到直线PM，再将线段AC所在的直线绕点C顺时针旋转 $α$ 得到直线CN，直线PM与直线CN相交于点Q．

(1)、当点P在线段BC上，当 $α = 60 °$ 时，如图1，直接判断 $\frac{B P}{C Q}$ 的大小，

(2)、当点P在线段BC上，当 $\frac{B C}{A C} = k$ 时，如图2，试判断线段 $\frac{B P}{C Q}$ 的大小，并说明理由；

(3)、当点P在直线BC上，当 $α = 90 °$ ， $A C = 8 \sqrt{2}$ ， $A P = 17$ 时，请利用备用图探究 $△ P C Q$ 面积的大小（直接写出结果即可）．

查看试题解析
26. 如图1，在平面直角坐标系中，直线AB： $y = - 3 x + 3$ 分别与y轴、x轴交于AB两点，直线AC交x轴于点C，且满足 $C O = 2 A O$ ．

(1)、求直线AC的表达式；

(2)、如图2，若点P为线段AC上一个动点，过点P作 $P D ⊥ x$ 轴，垂足为D，PD与直线AB交于点Q，当 $△ A P Q$ 的面积等于7时，求点P的坐标；

(3)、如图3，在（2）同的条件下，将 $△ C P D$ 沿x轴向右平移，记平移后的 $△ C P D$ 为 $△ C^{'} P^{'} D^{'}$ ，连接 $A P^{'}$ ， $B P^{'}$ ，当 $△ P^{'} A B$ 为直角三角形时，直接写出点 $P^{'}$ 的坐标．

查看试题解析

成绩/m	1.50	1.61	1.66	1.70	1.75	1.78
人数	2	3	2	1	5	1