辽宁省鞍山市铁东区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-07 类型:期中考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、三角形 B、等边三角形 C、平行四边形 D、菱形
-
2. 如果(x﹣y﹣2)(x﹣y+1)=0,那么x﹣y=( )A、2 B、﹣1 C、2或﹣1 D、﹣2或1
-
3. 如图所示,将△AOB绕点O按逆时针方向旋转45°后得到△A'OB',若∠AOB=15°,那么∠AOB'的度数是( )
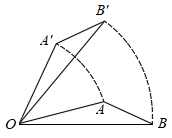 A、15° B、30° C、45° D、60°
A、15° B、30° C、45° D、60° -
4. 把方程x2+x=3(x﹣2)化成ax2+bx+c=0的形式,则a,b,c的值分别为( )A、1,﹣2,2 B、1,﹣3,6 C、1,﹣2,6 D、1,4,6
-
5. 如图,在平面直角坐标系中,点A坐标为(3,1),则sinα的值为( )
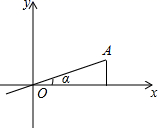 A、 B、 C、 D、
A、 B、 C、 D、 -
6. 函数y=﹣(x﹣2)2+1的图象可以由函数y=﹣x2的图象通过( )得到A、向左平移1个单位,再向上平移2个单位 B、向左平移1个单位,再向下平移2个单位 C、向右平移2个单位,再向上平移1个单位 D、向右平移2个单位,再向下平移1个单位
-
7. 如图,△ABC∽△ADE,且BC=2DE,则S四边形BEDC:S△ABC的值为( )
 A、1:4 B、3:4 C、2:3 D、1:2
A、1:4 B、3:4 C、2:3 D、1:2 -
8. 已知点A(x1 , y1),B(x2 , y2),C(x3 , y3)都在二次函数y=﹣x2+2x﹣1的图象上,且x1<x2<1<x3 , 则下列结论可能成立的是( )A、y1<y2<y3<0 B、0<y1<y2<y3 C、y1<y2<0<y3 D、y3<y2<y1<0
二、填空题
-
9. 在平面直角坐标系中,点M(﹣2,4)关于原点对称的点的坐标是 .
-
10. 某商场八月份销售额为100万元,十月份的销售额为121万元,求这个商场九、十月销售额的平均增长率,若设平均增长率为x,则可列方程为 .
-
11. 如图AB∥CD∥EF,若 , ,则 .

-
12. 若一元二次方程x2﹣4x﹣2=0的两个实数根为m,n,则 的值为 .
-
13. 《九章算术》中记载了一种测距的方法.如图,有座塔在河流北岸的点E处,一棵树位于河流南岸的点A处,从点A处开始,在河流南岸立4根标杆,以这4根标杆为顶点,组成边长为10米的正方形 ,且A,D,E三点在一条直线上,在标杆B处观察塔E,视线 与边 相交于点F,如果测得 米,那么塔与树的距离 为米.
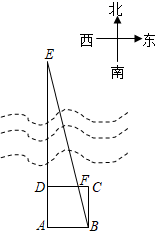
-
14. 若二次函数y=x2+3x+c的图象经过点A(0,c),过点A作x轴的平行线,与抛物线交于点B,则线段AB的长为 .
-
15. 二次函数y=ax2+bx+c(a≠0)的图象经过(﹣1,0),(0,4),(t,4)三点,当t≥3时,一元二次方程ax2+bx+c=n一定有实数根,则n的取值范围是 .
-
16. 如图,△ABC绕点B顺时针旋转得到△DBE,点A与点D对应,点C与点E对应,DB,DE分别与AC边交于G,F两点,连接BF,若DE垂直平分BC,下列结论:①∠E=30°;②BF⊥BE;③△ABG∽△DBF;④GF•BD=DG•BF.其中结论正确的是 . (填序号即可)
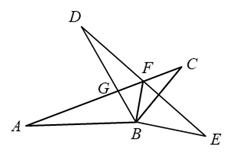
三、解答题
-
17. 解方程:(1)、x2+2x﹣7=0.(2)、2x2﹣3x+1=0.
-
18. 如图,已知△ABC三个顶点的坐标分别是A(2,4),B(1,2),C(4,1).按下列要求画出图形,并回答问题.
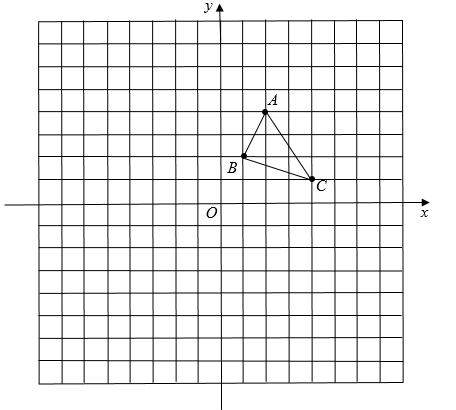
⑴画出△ABC绕点O逆时针旋转90°后得到的△A1B1C1 , 并写出点A1坐标.
⑵以O为位似中心,相似比为2,在y轴左侧将△ABC放大,得到△A2B2C2 , 在网格中画出△A2B2C2 .
-
19. 已知关于x的方程x2+kx+k-2=0,证明不论k为什么实数,这个方程总有两个不相等实数根.
-
20. 如图,在△ABC中,∠C=90°,∠A=45°,tan∠DBC= ,AB=4 ,求AD的长.
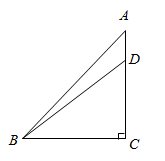
-
21. 已知二次函数y=x2﹣4x+3.
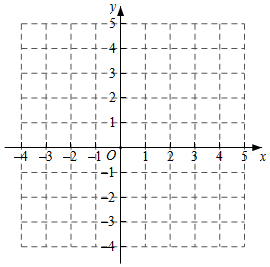 (1)、在平面直角坐标系xOy中,描出二次函数图象的顶点A,与x轴的交点B、C,并画出此二次函数的图象(不必列表);(2)、根据图象,直接写出当x<4时y的取值范围.
(1)、在平面直角坐标系xOy中,描出二次函数图象的顶点A,与x轴的交点B、C,并画出此二次函数的图象(不必列表);(2)、根据图象,直接写出当x<4时y的取值范围. -
22. 如图,将矩形ABCD绕着点C按顺时针方向旋转得到矩形FECG,点B与点E对应,点E恰好落在AD边上,BH⊥CE交于点H,求证:AB=BH.
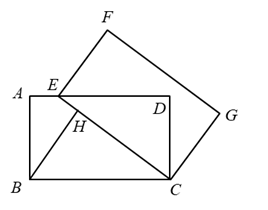
-
23. 如图,在Rt△ACB中,∠ACB=90°,点D为AB边上一点,且BC=CD,过D作DE⊥AB交AC于E.
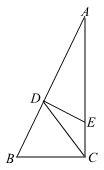 (1)、求证:△CDE∽△CAD;(2)、若BC=2,CE=1,求AD的长.
(1)、求证:△CDE∽△CAD;(2)、若BC=2,CE=1,求AD的长. -
24. 某水果捞店销售一款成本为12元/份的水果捞,若以30元/份的价格出售,每周可售出150份,“十一”黄金周降价促销,若销售单价每降低1元,则每周可多售出15份(销售单价不低于25元/份),设该款水果捞的销售单价为x元/份,“十一”黄金周的销售利润为y元.(1)、当销售单价为多少元/份时,“十一”黄金周的销售利润为2880元.(2)、当销售单价为多少元/份时,“十一”黄金周的销售利润最大,最大利润为多少元?
-
25. 如图,在平行四边形ABCD中,AD=AC,∠ADC=α,点E为射线BA上一动点,且AE<AB,连接DE,将线段DE所在直线绕点D顺时针旋转α交BA延长线于点H,DE所在直线与射线CA交于点G.
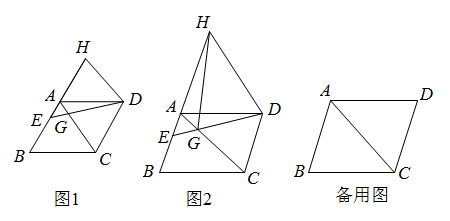 (1)、如图1,当α=60°时,求证:△ADH≌△CDG;(2)、当α≠60°时,
(1)、如图1,当α=60°时,求证:△ADH≌△CDG;(2)、当α≠60°时,①如图2,连接HG,求证:△ADC∽△HDG;
②若AB=9,BC=12,AE=3,请直接写出EG的长.
-
26. 如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与y轴交于点B(0,2),与x轴交于D,C(2,0)两点,点P为抛物线上一动点.
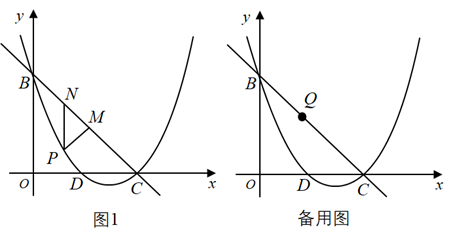 (1)、求抛物线的解析式.(2)、如图1,点P在直线BC下方抛物线上运动,PM⊥BC交于M,PN∥y轴交BC于N,当△PMN的周长最大时,求点P坐标.(3)、平面内一点Q(1,1),连接PB,PC,PQ,若PQ恰好平分∠BPC,请直接写出点P的横坐标.
(1)、求抛物线的解析式.(2)、如图1,点P在直线BC下方抛物线上运动,PM⊥BC交于M,PN∥y轴交BC于N,当△PMN的周长最大时,求点P坐标.(3)、平面内一点Q(1,1),连接PB,PC,PQ,若PQ恰好平分∠BPC,请直接写出点P的横坐标.
