江西省吉安市2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-07 类型:期中考试
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 如图,下列四个条件中,能判定平行四边形ABCD为菱形的是( )
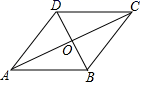 A、∠ADB=90° B、OA=OB C、OA=OC D、AB=BC3.
A、∠ADB=90° B、OA=OB C、OA=OC D、AB=BC3.如图所示,随机闭合开关K1 , K2 , K3中的两个,则能让两盏灯泡同时发光的概率为( )
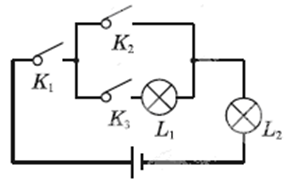 A、 B、 C、 D、4. 已知线段AB的长度为2,点C是线段AB的黄金分割点,则AC的长度为( )A、 B、 C、 或 D、 或5. 关于x的一元二次方程 有实数根,则k的取值范围是( )A、 B、 且 C、 D、 且6. 如图所示,在平面直角坐标系xOy中,将矩形OABC沿OB对折,使点A落在点 处,若点B的坐标为 ,则点 的坐标为( )
A、 B、 C、 D、4. 已知线段AB的长度为2,点C是线段AB的黄金分割点,则AC的长度为( )A、 B、 C、 或 D、 或5. 关于x的一元二次方程 有实数根,则k的取值范围是( )A、 B、 且 C、 D、 且6. 如图所示,在平面直角坐标系xOy中,将矩形OABC沿OB对折,使点A落在点 处,若点B的坐标为 ,则点 的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
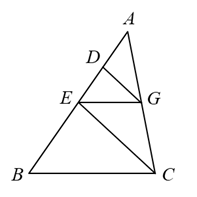
7. 若 ,则 .8. 已知 是一元二次方程 的两个根,且 ,则 .9. 如图所示,已知D为 边AB上一点, ,DE∥BC,交AC于E, ,则 .
 10. 从 三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率是 .11. 如图所示,在正方形ABCD中,点P在AC上, , ,垂足分别为E,F, ,则DP的长为 .
10. 从 三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率是 .11. 如图所示,在正方形ABCD中,点P在AC上, , ,垂足分别为E,F, ,则DP的长为 . 12. 在菱形ABCD中, , ,点P是射线BC上一动点,(不与B,C重合),连接PA,PD,当 是等腰三角形时,BP的长为 .
12. 在菱形ABCD中, , ,点P是射线BC上一动点,(不与B,C重合),连接PA,PD,当 是等腰三角形时,BP的长为 .三、解答题
-
13.(1)、解方程(2)、如图所示, 中, 求证:
 14. 已知 、 、 是 的三边长,且 .(1)、求 的值;(2)、若 的周长为90,求各边的长.15. 如图所示,四边形ABCD是正方形, 是等边三角形,请仅用无刻度的直尺分别按下列要求做图(保留作图痕迹).
14. 已知 、 、 是 的三边长,且 .(1)、求 的值;(2)、若 的周长为90,求各边的长.15. 如图所示,四边形ABCD是正方形, 是等边三角形,请仅用无刻度的直尺分别按下列要求做图(保留作图痕迹). (1)、在图1中,作CD的中点M.(2)、在图2中,在CD边上作一点N,使 .16. 已知关于x的一元二次方程ax2+bx+1=0(a≠0)有两个相等的实数根,求 的值.17. 已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形,
(1)、在图1中,作CD的中点M.(2)、在图2中,在CD边上作一点N,使 .16. 已知关于x的一元二次方程ax2+bx+1=0(a≠0)有两个相等的实数根,求 的值.17. 已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形,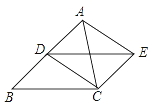 (1)、求证:四边形ADCE是平行四边形;
(1)、求证:四边形ADCE是平行四边形;
(2)、当△ABC满足什么条件时,平行四边形ADCE是矩形?18. 如图,有两部不同型号的手机(分别记为A,B)和与之匹配的2个保护盖(分别记为a,b)散乱地放在桌子上. (1)、若从手机中随机取一部,再从保护盖中随机取一个,求恰好匹配的概率;(2)、若从手机和保护盖中随机取两个,用画树状图法或列表法求恰好匹配的概率.19. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)、若从手机中随机取一部,再从保护盖中随机取一个,求恰好匹配的概率;(2)、若从手机和保护盖中随机取两个,用画树状图法或列表法求恰好匹配的概率.19. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.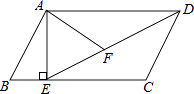 (1)、求证:△ADF∽△DEC;
(1)、求证:△ADF∽△DEC;
(2)、若AB=8,AD=6 ,AF=4 ,求AE的长.
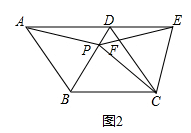
20. 因魔幻等与众不同的城市特质,以及抖音等新媒体的传播,重庆已成为国内外游客最喜欢的旅游目的地城市之一.著名“网红打卡地”磁器口在2018年五一长假期间,接待游客达20万人次,预计在2020年五一长假期间,接待游客将达28.8万人次.在磁器口老街,美食无数,一家特色小面店希望在五一长假期间获得好的收益,经测算知,该小面成本价为每碗6元,借鉴以往经验:若每碗卖25元,平均每天将销售300碗,若价格每降低1元,则平均每天多销售30碗.(1)、求出2018至2020年五一长假期间游客人次的年平均增长率;(2)、为了更好地维护重庆城市形象,店家规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天利润6300元?21.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
 (1)、证明:PC=PE;(2)、求∠CPE的度数;(3)、
(1)、证明:PC=PE;(2)、求∠CPE的度数;(3)、如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
 22. 如图,四边形ACDE是证明勾股定理时用到的图形,a,b,c是Rt△ABC和Rt△BED边长,易知AE= c,这时我们把关于x的形如ax2+ cx+b=0的一元二次方程称为“勾系一元二次方程”.
22. 如图,四边形ACDE是证明勾股定理时用到的图形,a,b,c是Rt△ABC和Rt△BED边长,易知AE= c,这时我们把关于x的形如ax2+ cx+b=0的一元二次方程称为“勾系一元二次方程”.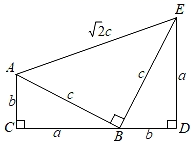 (1)、写出一个“勾系一元二次方程” .(2)、求证:关于x的“勾系一元二次方程”ax2+ cx+b=0必有实数根.(3)、若x=﹣1是“勾系一元二次方程”ax2+ cx+b=0的一个根,且△ABC的面积是25,求四边形ACDE的周长.23. 如图所示,点B坐标为 ,点A坐标为 ,动点P从点O开始沿OB以每秒1个单位长度的速度向点B移动,动点Q从点B开始沿BA以每秒2个单位长度的速度向点A移动,如果P,Q分别从O,B同时出发,用t(秒)表示移动的时间 .
(1)、写出一个“勾系一元二次方程” .(2)、求证:关于x的“勾系一元二次方程”ax2+ cx+b=0必有实数根.(3)、若x=﹣1是“勾系一元二次方程”ax2+ cx+b=0的一个根,且△ABC的面积是25,求四边形ACDE的周长.23. 如图所示,点B坐标为 ,点A坐标为 ,动点P从点O开始沿OB以每秒1个单位长度的速度向点B移动,动点Q从点B开始沿BA以每秒2个单位长度的速度向点A移动,如果P,Q分别从O,B同时出发,用t(秒)表示移动的时间 . (1)、用含t的式子来表示 . .(2)、当t为何值时,以点P、B、Q为顶点的三角形与 相似?(3)、若四边形OPQA的面积为y,试写出y与t的函数关系式,并求出t取何值时,四边形OPQA的面积最小?(4)、在y轴上是否存在点E,使点P、Q在移动过程中,以B、E、Q、P为顶点的四边形的面积是一个常数?若存在请求出点E的坐标;若不存在,请说明理由.
(1)、用含t的式子来表示 . .(2)、当t为何值时,以点P、B、Q为顶点的三角形与 相似?(3)、若四边形OPQA的面积为y,试写出y与t的函数关系式,并求出t取何值时,四边形OPQA的面积最小?(4)、在y轴上是否存在点E,使点P、Q在移动过程中,以B、E、Q、P为顶点的四边形的面积是一个常数?若存在请求出点E的坐标;若不存在,请说明理由.