黑龙江省齐齐哈尔市拜泉县2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-07 类型:期中考试
一、单选题
-
1. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
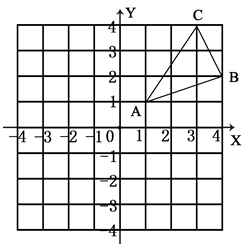
D、 2. 二次函数 的顶点坐标是( )A、(1,-3) B、(-1,-3) C、(1,3) D、(-1,3)3. 在平面直角坐标系中,点P(﹣1,2)关于原点的对称点的坐标为( )A、(﹣1,﹣2) B、(1,﹣2) C、(2,﹣1) D、(﹣2,1)4. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 如图,在⊙O中,A,B,D为⊙O上的点,∠AOB=52°,则∠ADB的度数是( )
2. 二次函数 的顶点坐标是( )A、(1,-3) B、(-1,-3) C、(1,3) D、(-1,3)3. 在平面直角坐标系中,点P(﹣1,2)关于原点的对称点的坐标为( )A、(﹣1,﹣2) B、(1,﹣2) C、(2,﹣1) D、(﹣2,1)4. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 如图,在⊙O中,A,B,D为⊙O上的点,∠AOB=52°,则∠ADB的度数是( ) A、104° B、52° C、38° D、26°6. 抛物线y=x2﹣2x+m与x轴有两个交点,则m的取值范围为( )A、m>1 B、m=1 C、m<1 D、m<47. 用配方法解一元二次方程 ,此方程可变形为( )A、 B、 C、 D、8. 二次函数y=x2﹣8x+1的最小值是( )
A、104° B、52° C、38° D、26°6. 抛物线y=x2﹣2x+m与x轴有两个交点,则m的取值范围为( )A、m>1 B、m=1 C、m<1 D、m<47. 用配方法解一元二次方程 ,此方程可变形为( )A、 B、 C、 D、8. 二次函数y=x2﹣8x+1的最小值是( )
A、4 B、﹣15 C、﹣4 D、159. 若关于x的一元二次方程(m﹣1)x2+x﹣1=0有实数根,则m的取值范围是( )A、m< B、m 且m≠1 C、m 且m≠1 D、m> 且m≠110. 如图,△ABC中,∠C=70°,∠B=30°,将△ABC绕点A顺时针旋转后,得到△AB´C´,且C´在边BC上,则∠B´C´B的度数为( ) A、30° B、40° C、46° D、60°
A、30° B、40° C、46° D、60°二、填空题
-
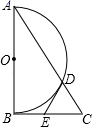
11. 二次函数y=﹣2x2+4x+1图象的开口方向是.12. 在你认识的图形中,写出一个既是轴对称又是中心对称的图形名称:.13. 方程(x﹣5)2=0的根是 .14. 若正六边形的外接圆半径长为4,则它的边长等于 .15. △ABC的两边长分别为2和3,第三边的长是方程x2-8x+15=0的根,则△ABC的周长是 .16. 如图, 是 的切线,切点为 是 的直径, 交 于点 ,连接 ,若 ,则 的度数为 .
 17. 抛物线 中,若y随x的增大而增大,则x的取值范围是 .18. 如图,CD是⊙O的直径,弦AB⊥CD,连接OA,OB,BD,若∠AOB=100°,则∠ABD =度.
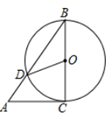
17. 抛物线 中,若y随x的增大而增大,则x的取值范围是 .18. 如图,CD是⊙O的直径,弦AB⊥CD,连接OA,OB,BD,若∠AOB=100°,则∠ABD =度.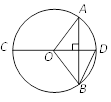 19. 有一扇形的铁皮,其半径为 ,圆心角为 ,若用此扇形铁皮围成一个圆锥形的教具(不计接缝),则此圆锥的高是 .20. 将二次函数 的图象向右平移2个单位,再向上平移1个单位,所得图象的表达式是 .
19. 有一扇形的铁皮,其半径为 ,圆心角为 ,若用此扇形铁皮围成一个圆锥形的教具(不计接缝),则此圆锥的高是 .20. 将二次函数 的图象向右平移2个单位,再向上平移1个单位,所得图象的表达式是 .三、解答题
-
21. 解下列方程:(1)、 ;(2)、 ;(3)、 ;(4)、 .22. 如图, , 分别与 相切于 两点,若 ,求 的度数.
 23. 已知函数 是二次函数.(1)、求 的值;(2)、写出这个二次函数图象的对称轴和顶点坐标.
23. 已知函数 是二次函数.(1)、求 的值;(2)、写出这个二次函数图象的对称轴和顶点坐标.