河北省邯郸市永年区2021-2022学年九年级上学期期中考试数学试题

试卷更新日期：2021-12-07 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四条线段中，不能成比例的是（）

A、 $a$ ＝2， $b$ ＝4， $c$ ＝3， $d$ ＝6 B、 $a$ ＝ $\sqrt{6}$ ， $b$ ＝ $\sqrt{3}$ ， $c$ ＝1， $d$ ＝ $\sqrt{2}$ C、 $a$ ＝6， $b$ ＝4， $c$ ＝10， $d$ ＝5 D、 $a$ ＝ $\sqrt{5}$ ， $b$ ＝2 $\sqrt{3}$ ， $c$ ＝ $\sqrt{15}$ ， $d$ ＝2

查看试题解析
2. 某中学规定学生的学期体育成绩满分100分，其中课外体育占20％，期中考试成绩占30％，期末考试成绩占50％．小彤的三项成绩（百分制）依次为95，90，94，则小彤这学期的体育成绩为（）

A、89 B、90 C、92 D、93

查看试题解析
3. 若方程 $(m + 3) x^{m^{2} - 7} + m x - 2 = 0$ 是关于 $x$ 的一元二次方程，则 $m$ 等于（）

A、 $\pm \sqrt{7}$ B、 $3$ C、-3 D、±3

查看试题解析
4. 下列计算错误的有（）
① $\sin 60 ° - \sin 30 ° = \sin 30 °$ ；② $\sin^{2} 45 ° + \cos^{2} 45 ° = 1$ ；③ $3 \tan^{2} 60 ° = \frac{1}{3}$ ；④ $4 \tan 30 ° = \frac{\cos 30 °}{\sin 30 °}$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 在解方程 $2 x^{2} + 4 x + 1 = 0$ 时，对方程进行配方，对于两人的做法，说法正确的是（）

小思：

$2 x^{2} + 4 x = - 1$

$x^{2} + 2 x = - \frac{1}{2}$

$x^{2} + 2 x + 1 = - \frac{1}{2} + 1$

${(x + 1)}^{2} = \frac{1}{2}$

小博

$2 x^{2} + 4 x = - 1$

$4 x^{2} + 8 x = - 2$

$4 x^{2} + 8 x + 4 = - 2 + 4$

${(2 x + 2)}^{2} = 2$

A、两人都正确 B、小思正确，小博不正确 C、小思不正确，小博正确 D、两人都不正确

查看试题解析
6. 如图， $A B$ 与 $C D$ 相交于点 $E$ ，点 $F$ 在线段 $B C$ 上，且 $A C / / E F / / D B$ ．若 $B E = 5$ ， $B F = 3$ ， $A E = B C$ ，则 $\frac{B D}{A C}$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{3}{5}$ D、 $\frac{2}{5}$

查看试题解析
7. 若一组数据4，x，5，y，7，9的平均数为6，众数为5，则这组数据的中位数为（）

A、5 B、6 C、5.5 D、6.5

查看试题解析
8. 用因式分解法把方程 $5 y (y - 3) = 3 - y$ 分解成两个一次方程，正确的是（）

A、 $y - 3 = 0 ， 5 y - 1 = 0$ B、 $5 y = 0 ， y - 3 = 0$ C、 $5 y + 1 = 0 ， y - 3 = 0$ D、 $5 y = 1 ， y - 3 = 3 - y$

查看试题解析
9. 如图，在 $△ A B C$ 中，点D、E分别在边 $A B$ 、 $A C$ 上，下列条件中能判断 $△ A B C \sim △ A E D$ 的是（）
① $∠ A E D = ∠ B$ ；② $∠ A D E = ∠ C$ ；③ $\frac{A D}{A E} = \frac{A C}{A B}$ ；④ $\frac{A D}{A B} = \frac{A E}{A C}$ .

A、①② B、①②③ C、①②④ D、①②③④

查看试题解析
10. 设 $x_{1} ， x_{2}$ 是一元二次方程 $x^{2} - 2 x - 3 = 0$ 的两根，则 $\frac{3}{x_{1}} + \frac{3}{x_{2}} =$ （）

A、-2 B、2 C、3 D、-3

查看试题解析
11. 甲、乙、丙、丁四人10次随堂测验的成绩如图所示，从图中可以看出这10次测验平均成绩较高且较稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
12. 如图，已知 $△ A B C$ ，任取一点O，连接 $A O ， B O ， C O$ ，并取它们的中点D，E，F，得 $△ D E F$ ，则下列说法正确的有（）
① $△ A B C$ 与 $△ D E F$ 是位似图形；② $△ A B C$ 与 $△ D E F$ 是相似图形；③ $△ A B C$ 与 $△ D E F$ 的周长比为1：2；④若 $△ A B C$ 的面积为4，则 $△ D E F$ 的面积为1．

A、1个 B、2个 C、3个 D、4个

查看试题解析
13. 如图，在△ABC中，∠ACB＝90°，点D在AB的延长线上，连接CD，若AB＝2BD， $\tan ∠ B C D = \frac{2}{3}$ ，则 $\frac{A C}{B C}$ 的值为（）

A、1 B、2 C、 $\frac{1}{2}$ D、 $\frac{3}{2}$

查看试题解析
14. 如图，有一块锐角三角形材料，边 $B C = 120 m m$ ，高 $A D = 90 m m$ ，要把它加工成矩形零件，使其一边在 $B C$ 上，其余两个顶点分别在 $A B$ ， $A C$ ，且 $E H = 2 E F$ ，则这个矩形零件的长为 $($ $)$

A、 $36 m m$ B、 $80 m m$ C、 $40 m m$ D、 $72 m m$

查看试题解析
15. 如图，为了测量某建筑物BC的高度，某数学兴趣小组采用了如下的方法：先从与建筑物底端B在同一水平线上的A点出发，先沿斜坡AD行走390米至坡顶D处，再从D处沿水平方向继续前行一定距离后至点E处，在E点处测得该建筑物顶端C的仰角为68°，建筑物底端B的俯角为57°，其中A、B、C、D、E在同一平面内，斜坡AD的坡度i＝1：2.4，根据数学兴趣小组的测量数据，计算得出建筑物BC的高度约为（　　）（计算结果精确到0.1米，参考数据：sin68°≈0.93，tan68°≈2.48，sin57°≈0.84，tan57°≈1.54）

A、241.6米 B、391.6米 C、422.9米 D、572.9米

查看试题解析
16. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
①若 $a + b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；③若 $c$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$

其中正确的是（）

A、只有①② B、只有①②④ C、只有①③④ D、只有①②③

查看试题解析

二、填空题

17. 甲、乙两人各射击6次，甲所中的环数是8，5，5， $a$ ， $b$ ， $c$ ，且甲所中的环数的平均数是6，众数是8；乙所中的环数的平均数是6，方差是4．根据以上数据，对甲、乙射击成绩的稳定的是．

查看试题解析
18. 如图，在5×5的正方形网格中，每个小正方形的边长均为1，点A、B、C都在格点上，则cos∠BAC的值为．

查看试题解析
19. 如图，矩形鸡场平面示意图，一边靠墙，墙长 $8 m$ ，另外三面用竹篱笆图成，若竹篱笆总长为 $27 m$ ，所围的面积为 $70 m^{2}$ ，则此矩形鸡场中，平行于墙面的竹篱笆边长为 $m$ ．

查看试题解析
20. 如图，已知： $∠ A C B = ∠ A D C = 90^{\circ}$ ， $A D = 2$ ， $C D = \sqrt{2}$ ，当 $A B$ 的长为时， $△ A C B$ 与 $△ A D C$ 相似．

查看试题解析

三、解答题

21. 按要求解下列方程：

(1)、 $5 x^{2} - 3 x = x + 1$ （公式法）

(2)、 $x^{2} - 8 x = 4$ （配方法）

(3)、2x（x﹣3）＝9﹣3x （因式分解法）

查看试题解析

22. 某中学举行“中国梦”校园好声音歌手比赛，初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，根据这10人的决赛成绩（满分为100分），制作了如下统计图：

(1)、根据上图提供的数据填空：

	平均数	中位数	众数	方差
初中部	*	85	$b$	70
高中部	85	$a$	100	*

$a$ 的值是， $b$ 的值是；

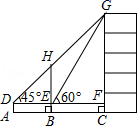
(2)、结合两队的平均数和中位数，分析哪个队的决赛成绩好；

(3)、根据题（1）中的数据，试通过计算说明，哪个代表队的成绩比较稳定？

查看试题解析

23. 如图，直立在B处的标杆AB＝2.4m，直立在F处的观测者从E处看到标杆顶A、树顶C在同一条直线上（点F，B，D也在同一条直线上）．已知BD＝8m，FB＝2.5m，人高EF＝1.5m，求树高CD．

查看试题解析
24. 商场某种商品平均每天可销售30件，每件盈利50元，为了尽快减少库存，商场决定采取适当的降价措施．经调查发现，每件商品每降价1元，商场平均每天可多售出2件．

(1)、若某天该商品每件降价3元，当天可获利多少元？

(2)、设每件商品降价x元，则商场日销售量增加件，每件商品，盈利元(用含x的代数式表示)；

(3)、在上述销售正常情况下，每件商品降价多少元时，商场日盈利可达到2000元？

查看试题解析
25. 如图，某数学兴趣小组为测量一棵古树BH和教学楼CG的高，先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°，此时教学楼顶端G恰好在视线DH上，再向前走7米到达B处，又测得教学楼顶端G的仰角∠GEF为60°，点A、B、C三点在同一水平线上．

(1)、计算古树BH的高；

(2)、计算教学楼CG的高．（参考数据： $\sqrt{2}$ ≈14， $\sqrt{3}$ ≈1.7）

查看试题解析
26. 已知：如图，在菱形 $A B C D$ 中，点 $E$ ， $F$ 分别在边 $A B$ ， $A D$ 上， $B E = D F$ ， $C E$ 的延长线交 $D A$ 的延长线于点 $G$ ， $C F$ 的延长线交 $B A$ 的延长线于点 $H$ ．

(1)、求证： $△ B E C ~ △ B C H$ ；

(2)、如果 $B E^{2} = A B \cdot A E$ ，求证： $A G = D F$ ．

查看试题解析