河北省沧州市东光县2021-2022学年九年级上学期期中数学试题
试卷更新日期:2021-12-07 类型:期中考试
一、单选题
-
1. 下列方程,是一元二次方程一般形式的是( )A、 B、 C、 D、2. 已知 是 的弦, 的半径为r , 下列关系式一定成立的是( )A、 B、 C、 D、3. 下列图形中, 为圆心角的是( )A、
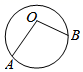 B、
B、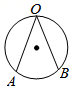 C、
C、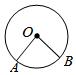 D、
D、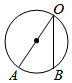 4. 抛物线 的对称轴是( )A、直线 B、直线 C、直线 D、直线5. 下列图形是中心对称图形的是( )A、
4. 抛物线 的对称轴是( )A、直线 B、直线 C、直线 D、直线5. 下列图形是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 已知 的半径为5,点 在 内,则 的长可能是( )A、7 B、6 C、5 D、47. 点A(﹣3,a)与点B(3,4)关于原点对称,则a的值为( )A、﹣3 B、﹣4 C、3 D、48. 如图, 与 关于O成中心对称,下列结论中不一定成立的是( )
6. 已知 的半径为5,点 在 内,则 的长可能是( )A、7 B、6 C、5 D、47. 点A(﹣3,a)与点B(3,4)关于原点对称,则a的值为( )A、﹣3 B、﹣4 C、3 D、48. 如图, 与 关于O成中心对称,下列结论中不一定成立的是( ) A、 B、 C、 D、9. 若二次函数 的图象如图所示,则坐标原点可能是( )
A、 B、 C、 D、9. 若二次函数 的图象如图所示,则坐标原点可能是( ) A、P点 B、Q点 C、M点 D、N点10. 要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排10天,每天安排4场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为( )A、 B、 C、 D、11. 将抛物线 向左平移1个单位,再向下平移3个单位得到的解析式是( )A、 B、 C、 D、12. 如图,在平面直角坐标系中,平行于x轴的直线 ,与二次函数 , 分别交于A、B和C、D,若 ,则a为( )
A、P点 B、Q点 C、M点 D、N点10. 要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据场地和时间等条件,赛程计划安排10天,每天安排4场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为( )A、 B、 C、 D、11. 将抛物线 向左平移1个单位,再向下平移3个单位得到的解析式是( )A、 B、 C、 D、12. 如图,在平面直角坐标系中,平行于x轴的直线 ,与二次函数 , 分别交于A、B和C、D,若 ,则a为( )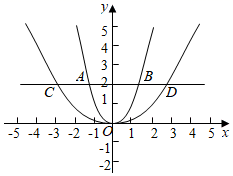 A、4 B、 C、2 D、13. 若关于x的方程 的解是 , (a,m,b均为常数, ),则方程 的解是( )A、 , B、 , C、 , D、 ,14. 已知在正六边形ABCDEF中,P是EF的中点,若阴影部分四边形ABPE的面积为9,则五边形BCDEP的面积是( )
A、4 B、 C、2 D、13. 若关于x的方程 的解是 , (a,m,b均为常数, ),则方程 的解是( )A、 , B、 , C、 , D、 ,14. 已知在正六边形ABCDEF中,P是EF的中点,若阴影部分四边形ABPE的面积为9,则五边形BCDEP的面积是( ) A、12 B、 C、18 D、15. 当 时,关于x的一元二次方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定16. 已知O是 的外心,连接AO并延长交BC于D, ,过D作 于E,若 ,则AC的长为( )
A、12 B、 C、18 D、15. 当 时,关于x的一元二次方程 的根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定16. 已知O是 的外心,连接AO并延长交BC于D, ,过D作 于E,若 ,则AC的长为( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
17. 经过两点可以做个圆,不在同一直线的个点可以确定一个圆.18. 若将方程x2-6x=7化为(x+m)2=b的形式,则m= , b= .19. 如图,一段抛物线: ,记为 ,它与 轴交于点 , ;将 绕点 旋转 得 ,交 轴于点 ;将 绕点 旋转 得 ,交 轴于点 ;…,如此进行下去,直至得 .
 (1)、请写出抛物线 的解析式:;(2)、若 在第10段抛物线 上,则 .
(1)、请写出抛物线 的解析式:;(2)、若 在第10段抛物线 上,则 .三、解答题
-
20. 如图,在边长为1的小正方形组成的网格中,点A,B,O都在格点上.

⑴作出点A关于点O的对称点 ;
⑵连接 ,画出线段 绕点 顺时针旋转 后得到的对应线段 .
21. 如图,已知 是等腰直角三角形,B为AE上一点, 经过旋转到达 的位置,问: (1)、旋转中心是哪个点?旋转了多少度?(2)、求 的度数.22. 如图,已知四边形ABCD内接于圆O,连接BD, , .
(1)、旋转中心是哪个点?旋转了多少度?(2)、求 的度数.22. 如图,已知四边形ABCD内接于圆O,连接BD, , . (1)、求证: ;(2)、若圆O的半径为3,求BC的长.23. 已知:如图,在 中, , , .点P从点A开始沿AB边向点B以1 cm/s的速度移动,同时点Q从点B开始沿BC边向点C以2 cm/s的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为x秒,
(1)、求证: ;(2)、若圆O的半径为3,求BC的长.23. 已知:如图,在 中, , , .点P从点A开始沿AB边向点B以1 cm/s的速度移动,同时点Q从点B开始沿BC边向点C以2 cm/s的速度移动.当一个点到达终点时另一点也随之停止运动,设运动时间为x秒, (1)、求几秒后, 的面积等于 ?(2)、求几秒后,PQ的长度等于5cm?24. 如图,已知二次函数 的图象经过点 , .
(1)、求几秒后, 的面积等于 ?(2)、求几秒后,PQ的长度等于5cm?24. 如图,已知二次函数 的图象经过点 , .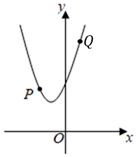 (1)、求b和c的值;(2)、点 在该二次函数图象上,当 时,该二次函数有最小值11,请根据图象求出m的值.25. 如图1所示,在 中, , ,P是BC边上一点(不与B、C点重合),将线段AP绕点A逆时针旋转 得到扇形PAQ.
(1)、求b和c的值;(2)、点 在该二次函数图象上,当 时,该二次函数有最小值11,请根据图象求出m的值.25. 如图1所示,在 中, , ,P是BC边上一点(不与B、C点重合),将线段AP绕点A逆时针旋转 得到扇形PAQ. (1)、求证:(2)、当BC与扇形PAQ相切时,求BQ的长;(3)、如图2,若 ,求阴影部分的图形的周长.(结果不求近似值)26. 某商场销售甲、乙两种产品,其中甲商品进价为20元. 在销售过程中发现,甲商品每天的销售利润w1(单位:个)与其销售单价x(单位:元)有如下关系:w1=-x2+bx-1260,当x=30时,w1=330;乙商品每天的销售利润w2(单位:个)与其销售单价z(单位:元)有如下关系w2=-z2+102z+c,当z=50时,w2=440.其中x、z均为整数,并且销售单价均高于进价.(1)、求b,c的值;(2)、若乙商品销售单价为甲商品销售单价的1.5倍,当两种商品每天获得的利润相同时,甲、乙两种商品销售单价分别为多少;(3)、若乙商品销售单价为甲商品销售单价的2倍,当这两种商品每天销售利润的和最大时,请直接写出此时甲的销售单价.
(1)、求证:(2)、当BC与扇形PAQ相切时,求BQ的长;(3)、如图2,若 ,求阴影部分的图形的周长.(结果不求近似值)26. 某商场销售甲、乙两种产品,其中甲商品进价为20元. 在销售过程中发现,甲商品每天的销售利润w1(单位:个)与其销售单价x(单位:元)有如下关系:w1=-x2+bx-1260,当x=30时,w1=330;乙商品每天的销售利润w2(单位:个)与其销售单价z(单位:元)有如下关系w2=-z2+102z+c,当z=50时,w2=440.其中x、z均为整数,并且销售单价均高于进价.(1)、求b,c的值;(2)、若乙商品销售单价为甲商品销售单价的1.5倍,当两种商品每天获得的利润相同时,甲、乙两种商品销售单价分别为多少;(3)、若乙商品销售单价为甲商品销售单价的2倍,当这两种商品每天销售利润的和最大时,请直接写出此时甲的销售单价.