广东省湛江市麻章区2020-2021学年九年级上学期期中数学试题

试卷更新日期：2021-12-07 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图标中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程是一元二次方程的是（）

A、 $x^{2} - y = 1$ B、 $x^{2} + 2 x - 3 = 0$ C、 $x^{2} + \frac{1}{x} = 3$ D、 $x - 5 y = 6$

查看试题解析
3. 下列命题中错误的是（）

A、圆是轴对称图形，任何一条直径所在直线都是圆的对称轴 B、圆是中心对称图形，圆心是它的对称中心 C、图形经过旋转所得的对应点到旋转中心的距离相等 D、平分弦的直径一定垂直于这条弦

查看试题解析
4. 如图，将△ABC绕点A顺时针旋转60°得到△AED，若AB=4，AC=3，BC=2，则BE的长为（）

A、5 B、4 C、3 D、2

查看试题解析
5. 如图， $C D$ 是 $⊙ O$ 的直径，弦 $A B ⊥ C D$ 于点 $E$ ，连接 $B C$ 、 $B D$ ，下列结论中不一定正确的是（）

A、 $A E = B E$ B、 $\overset{⌢}{A D} = \overset{⌢}{B D}$ C、 $O E = D E$ D、 $\overset{⌢}{A C} = \overset{⌢}{B C}$

查看试题解析
6. 由二次函数 $y = 2 {(x - 3)}^{2} + 1$ ，可知（）

A、其图象的开口向下 B、其图象的对称轴为直线x=-3 C、其最小值为1 D、当x<3时，y随x的增大而增大

查看试题解析
7. 方程x²﹣9x+18=0的两个根是等腰三角形的底和腰，则这个三角形的周长为（）

A、12 B、15 C、12或15 D、不能确定

查看试题解析
8. 如图，在Rt $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A B C = 30 °$ ，将 $△ A B C$ 绕点 $C$ 顺时针旋转 $α$ 角 $(0 ° < α < 180 °)$ 至 $△ A^{'} B^{'} C$ ，使得点 $A^{'}$ 恰好落在 $A B$ 边上，则 $α$ 等于（）

A、 $150 °$ B、 $90 °$ C、 $30 °$ D、 $60 °$

查看试题解析
9. 若a，b是方程 $x^{2} + 2 x - 2016 = 0$ 的两根，则 $a^{2} + 3 a + b =$ （）

A、2016 B、2017 C、2014 D、2019

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，对称轴为 $x = 1$ ．给出以下结论：① $a b c > 0$ ；② $b^{2} > 4 a c$ ；③ $4 a + 2 b + c > 0$ ；④ $3 a + c > 0$ ．其中，正确的结论有（）

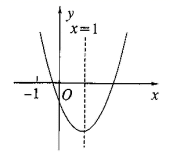A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 已知 $x = 1$ 是方程 $x^{2} + a x + 3 = 0$ 的一个根，则 $a$ 的值为

查看试题解析
12. 二次函数y=3（x﹣3）²+2顶点坐标坐标．

查看试题解析
13. 如图，⊙O是△ABC的外接圆，连结OA、OB，若∠AOB=70°，则∠ACB的度数为．

查看试题解析
14. 方程 $(n - 3) x^{| n | - 1} + 3 x + 3 n = 0$ 是关于x的一元二次方程，则 $n =$ ．

查看试题解析
15. 如图所示，P是正方形ABCD 内一点，将△ABP绕点B按顺时针方向旋转能与△CBP'重合，若PB＝3，则PP'＝

查看试题解析
16. 抛物线的部分图象如图所示，则当y＞0时，x的取值范围是．

查看试题解析
17. 如图，在平面直角坐标系中，⊙P的圆心是（4，a）且（a>2）半径为4，函数 $y = x$ 的图像被⊙P截得的弦AB的长为 $4 \sqrt{3}$ ，则a的值是．

查看试题解析

三、解答题

18. 解方程： $x^{2} + x - 1 = 0$

查看试题解析
19. △ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．按要求作图：

⑴画出△ABC关于原点O的中心对称图形△A₁B₁C₁；

⑵画出将△ABC绕点A逆时针旋转90°得到△AB₂C₂ ，

⑶△A₁B₁C₁中顶点A₁坐标为▲ ．

查看试题解析
20. 汽车产业的发展，有效促进我国现代化建设.某汽车销售公司2016年盈利1500万元，到2018年盈利2160万元，且从2016年到2018年，每年盈利的年增长率相同.

(1)、求平均年增长率？

(2)、若该公司盈利的年增长率继续保持不变，预计2019年盈利多少万元？

查看试题解析
21. 如图点O是等边 $△ ABC$ 内一点， $∠ A O B = 110^{°} ， ∠ B O C = α$ ，∠ACD=∠BCO，OC=CD，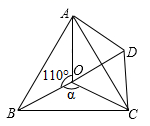

(1)、试说明： $△ COD$ 是等边三角形；

(2)、当 $α = 150^{°}$ 时，试判断 $△ A O D$ 的形状，并说明理由；

(3)、当 $∠ B O C$ 为多少度时， $△ A O D$ 是等腰三角形

查看试题解析
22. 已知关于 $x$ 的方程 $x^{2} - 2 x + 2 k - 1 = 0$ 有实数根．

(1)、求 $k$ 的取值范围；

(2)、设方程的两根分别是 $x_{1}$ 、 $x_{2}$ ，且 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}} = x_{1} \cdot x_{2}$ ，试求k的值．

查看试题解析
23. 如图，CD为圆O的直径，CD⊥AB，垂足为F，AO⊥BC，垂足为E，连接AC．

(1)、求∠B的度数．

(2)、若 $C E = 4 \sqrt{3}$ ，求圆O的半径．

查看试题解析
24. 某商店经营儿童益智玩具，已知成批购进时的单价是20元．调查发现：销售单价是30元时，月销售量是230件，而销售单价每上涨1元，月销售量就减少10件，但每件玩具售价不能高于40元．设每件玩具的销售单价上涨了x元时，月销售利润为y元．

(1)、求y与x的函数关系式并直接写出自变量x的取值范围；

(2)、每件玩具的售价定为多少元时，月销售利润恰为2520元？

(3)、每件玩具的售价定为多少元时可使月销售利润最大？最大的月利润是多少？

查看试题解析
25. 如图，抛物线顶点P（1，4），与y轴交于点C（0，3），与x轴交于点A，B．

(1)、求抛物线的解析式．

(2)、Q是抛物线上除点P外一点，△BCQ与△BCP的面积相等，求点Q的坐标．

(3)、若M，N为抛物线上两个动点，分别过点M，N作直线BC的垂线段，垂足分别为D，E．是否存在点M，N使四边形MNED为正方形？如果存在，求正方形MNED的边长；如果不存在，请说明理由．

查看试题解析