广东省梅州市大埔县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-12-07 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，不是一元二次方程的是（）

A、2x²+7＝0 B、2x²+2x+1＝0 C、5x²+ $\frac{1}{x}$ +4＝0 D、3x²+1＝7x

查看试题解析
2. 如图，菱形 $A B C D$ 的对角线 $B D = 12$ ， $A C = 10$ ，则该菱形的面积为（）．

A、60 B、80 C、100 D、120

查看试题解析

3. 在一个不透明的口袋里，装有仅颜色不同的黑球、白球若干只，某小组做摸球实验：将球搅匀后从中随机摸出一个，记下颜色，再放入袋中，不断重复，右表是活动中的一组数据，则摸到白球的概率约是（）

摸球的次数n	100	150	200	500	800	1000
摸到白球的次数m	58	96	116	295	484	601
摸到白球的概率	0.58	0.64	0.58	0.59	0.605	0.601

A、0.4 B、0.5 C、0.6 D、0.7

查看试题解析

4. 一个盒子中装有标号为1，2，3，4，5的五个小球，这些球除标号外都相同，从中随机摸出两个小球，则摸出的小球标号之和大于5的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
5. 如图，在△ABC中，D、E分别为AB、AC边上的点，DE∥BC，点F为BC边上一点，连接AF交DE于点G，则下列结论中一定正确的是（）

A、 $\frac{A D}{A B} = \frac{A E}{E C}$ B、 $\frac{A G}{G F} = \frac{A E}{B D}$ C、 $\frac{G E}{F C} = \frac{A D}{A B}$ D、 $\frac{A G}{A F} = \frac{A C}{E C}$

查看试题解析
6. 若矩形ABCD∽矩形EFGH，相似比为2∶3，已知AB＝3 cm，BC＝5 cm，则矩形EFGH的周长是（）

A、16 cm B、12 cm C、24 cm D、36 cm

查看试题解析
7. 一元二次方程x²﹣10x+21＝0的两根恰好是等腰三角形的底边长和腰长，则该等腰三角形的周长为（）

A、13 B、17 C、13或17 D、不能确定

查看试题解析
8. 若关于x的一元二次方程 $a x^{2} + b x + 1 = 0 (a \neq 0)$ 的一个解是 $x = 1$ ，则 $2020 - a - b$ 的值是（）

A、2025 B、2015 C、2021 D、2019

查看试题解析
9. 某市严格落实国家节水政策，2018年用水总量为6.5亿立方米，2020年用水总量为5.265亿立方米.设该市用水总量的年平均降低率是x，那么x满足的方程是（）

A、 $6.5 {(1 - x)}^{2} = 5.265$ B、 $6.5 {(1 + x)}^{2} = 5.265$ C、 $5.265 {(1 - x)}^{2} = 6.5$ D、 $5.265 {(1 + x)}^{2} = 6.5$

查看试题解析
10. 如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3BE，P是AC上一动点，则PB+PE的最小值是（）

A、8 B、9 C、10 D、8

查看试题解析

二、填空题

11. 方程 $x^{2} = - 2 x$ 的根是．

查看试题解析
12. 如图，l₁ $∥$ l₂ $∥$ l₃ ，直线a，b与l₁ ， l₂ ， l₃分别相交于点A、B、C和点D、E、F， $\frac{A B}{B C} = \frac{2}{3}$ ，DE＝4，则EF的长是．

查看试题解析
13. 已知关于 $x$ 的方程 $a x^{2} + 2 x - 3 = 0$ 有两个不相等的实数根，则 $a$ 的取值范围是．

查看试题解析
14. 如图，长方形内有两个相邻的正方形，其面积分别为 $2$ 和 $8$ ，则图中阴影部分的面积为

查看试题解析
15. 从分别标有A、B、C的3根纸签中随机抽取一根，然后放回，再随机抽取一根，两次抽签的所有可能结果的树形图如下：

那么抽出的两根签中，一根标有A，一根标有C的概率是．

查看试题解析
16. 如图，已知菱形ABCD的一个内角∠BAD=80°，对角线AC，BD相交于点O，点E在AB上，且BE=BO，则∠EOA=°.

查看试题解析
17. 如图，∠AOB＝30°，OC平分∠AOB，P为OC上一点，PD∥OA交OB于点D，PE⊥OA于E，OD＝4cm，则PE＝．

查看试题解析
18. 如图，在△ABC中，D是BC的中点，E是AD的中点，过点A作AF∥BC，AF与CE的延长线相交于点F，连接BF．

(1)、求证：四边形AFBD是平行四边形；

(2)、将下列命题填写完整，并使命题成立（图中不再添加其它的点和线）：
①当△ABC满足条件AB＝AC时，四边形AFBD是形；

② 当△ABC满足条件时，四边形AFBD是正方形．

查看试题解析

三、解答题

19. 解方程：

(1)、x²﹣3x＝0；

(2)、x²﹣2x＝4．

查看试题解析
20. 如图，在矩形ABCD中，AB＝6，BC＝8，沿直线MN对折，使A、C重合，直线MN交AC于O．求证：△COM∽△CBA．

查看试题解析
21. 随着信息技术的迅猛发展，人们去商场购物的支付方式更加多样、便捷．某校数学兴趣小组设计了一份调查问卷，要求每人选且只选一种你最喜欢的支付方式．现将调查结果进行统计并绘制成如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：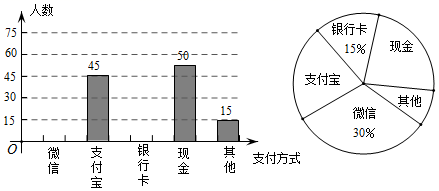

(1)、这次活动共调查了人；在扇形统计图中，表示“支付宝”支付的扇形圆心角的度数为；

(2)、将条形统计图补充完整．观察此图，支付方式的“众数”是“”；

(3)、在一次购物中，小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付，请用画树状图或列表格的方法，求出两人恰好选择同一种支付方式的概率．

查看试题解析
22. 如图，E，F是正方形ABCD的对角线AC上的两点，且AE＝CF.

(1)、求证：四边形BEDF是菱形；

(2)、)若正方形ABCD的边长为4，AE＝ $\sqrt{2}$ ，求菱形BEDF的面积.

查看试题解析

23. 一只不透明的袋子中装有

4

个质地、大小均相同的小球，这些小球分别标有数字

3 、 4 、 5 、 x

，甲、乙两人每次同时从袋中各随机摸出

1

个球，并计算摸出的这

2

个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复实验．实验数据如下表

摸球总次数	$10$	$20$	$30$	$60$	$90$	$120$	$180$	$240$	$330$	$450$
“和为 $8$ ”出现的频数	$2$	$10$	$13$	$24$	$30$	$37$	$58$	$82$	$110$	$150$
“和为 $8$ ”出现的频率	$0.20$	$0.50$	$0.43$	$0.40$	$0.33$	$0.31$	$0.32$	$0.34$	$0.33$	$0.33$

解答下列问题：

(1)、如果实验继续进行下去，根据上表数据，出现“和为

8

”的频率将稳定在它的概率附近．估计出现“和为

8

”的概率是；

(2)、如果摸出的这两个小球上数字之和为

9

的概率是

\frac{1}{3}

，那么x的值可以取

7

吗？请用列表法或画树状图法说明理由；如果x的值不可以取

7

，请写出一个符合要求的x值．

查看试题解析

24. 已知关于x的一元二次方程x²﹣（m+2）x+2m＝0．

(1)、证明：不论m为何值时，方程总有实数根．

(2)、若方程的两个实数根x₁ ， x₂满足x₁+x₂﹣x₁x₂＝4，求m的值．

查看试题解析
25. 习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气”．某校为响应我市全民阅读活动，利用节假日面向社会开放学校图书馆．据统计，第一个月进馆 $128$ 人次，进馆人次逐月增加，到第三个月末累计进馆 $608$ 人次，若进馆人次的月平均增长率相同．

(1)、求进馆人次的月平均增长率；

(2)、因条件限制，学校图书馆每月接纳能力不超过 $500$ 人次，在进馆人次的月平均增长率不变的条件下，校图书馆能否接纳第四个月的进馆人次，并说明理由．

查看试题解析