广东省广州市花都区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-12-07 类型：期中考试

进入出卷网下载

一、单选题

1. 垃圾分类一小步，低碳生活一大步，垃圾桶上常有以下四种垃圾分类标识的图案和文字说明，其中图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 关于x的一元二次方程2x²﹣4x﹣1＝0的二次项系数和一次项系数分别是（）

A、﹣2，4 B、﹣2，﹣1 C、2，4 D、2，﹣4

查看试题解析
3. 将抛物线y＝﹣2x²向左平移1个单位长度，再向下平移2个单位长度，所得到的抛物线解析式为（）

A、y＝﹣2（x﹣1）²﹣2 B、y＝﹣2（x+1）²﹣2 C、y＝﹣2（x﹣1）²+2 D、y＝﹣2（x+1）²+2

查看试题解析
4. 一元二次方程x²﹣6x＝﹣5配方后可变形为（）

A、（x﹣3）²＝4 B、（x+3）²＝4 C、（x﹣3）²＝13 D、（x+3）²＝13

查看试题解析
5. 抛物线y＝（x+1）²+2上两点（0，a）、（﹣1，b），则a、b的大小关系是（）

A、a＞b B、b＞a C、a＝b D、无法比较大小

查看试题解析
6. 如图，将△AOB绕着点O顺时针旋转，得到△COD，若∠AOB＝40°，∠BOC＝25°，则旋转角度是（）

A、25° B、15° C、65° D、40°

查看试题解析
7. 由二次函数 $y = 2 {(x - 3)}^{2} + 1$ ，可知（）

A、其图象的开口向下 B、其图象的对称轴为直线x=-3 C、其最小值为1 D、当x<3时，y随x的增大而增大

查看试题解析
8. 参加一次绿色有机农产品交易会的每两家公司都签订了一份合同，所有公司共签订了45份合同，如果参加这次交易会的公司共有x家，则根据题意列出的方程是（）

A、x（x﹣1）＝45 B、 $\frac{1}{2}$ x（x﹣1）＝45 C、x（x+1）＝45 D、 $\frac{1}{2}$ x（x+1）＝45

查看试题解析
9. 在同一坐标系中，一次函数y=ax+2与二次函数y=x²+a的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在平面直角坐标系中，有一个 $R t △ A O B$ ，∠ABO＝90°，∠AOB＝30°，直角边OB在y轴正半轴上，点A在第一象限，且OA＝1，将 $R t △ A O B$ 绕原点逆时针旋转30°，同时把各边长扩大为原来的两倍（即OA₁＝2OA）．得到 $R t △ O A_{1} B_{1}$ ，同理，将 $R t △ O A_{1} B_{1}$ 绕原点O逆时针旋转30°，同时把各边长扩大为原来的两倍，得到 $R t △ O A_{2} B_{2}$ ，…，依此规律，得到 $R t △ O A_{2021} B_{2021}$ ，则 $O B_{2021}$ 的长度为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\sqrt{3}$ ×2²⁰²⁰ C、 $\sqrt{3}$ ×2²⁰²¹ D、 $\sqrt{3}$ ×2²⁰¹⁹

查看试题解析

二、填空题

11. 在平面直角坐标系中，点（﹣2，3）关于原点对称的点的坐标是．

查看试题解析
12. 如图是二次函数y＝ax²+bx+c（a≠0）的图象，图象过点A(﹣3，0)对称轴为直线x＝﹣1，求另一个与x轴的交点坐标是．

查看试题解析
13. 如图所示，在正方形ABCD中，AC，BD相交于点O， $△$ AOE绕点O逆时针旋转90°后与 $△$ BOF重合，AB＝2，则四边形BEOF面积是．

查看试题解析
14. 若抛物线y＝x²﹣6x+m与x轴有两个公共点，则m的取值范围是．

查看试题解析
15. 已知 $m$ 是关于 $x$ 的方程 $x^{2} - 2 x - 5 = 0$ 的一个根，则 $3 m^{2} - 6 m =$ ．

查看试题解析
16. 如图，抛物线y＝ax²+bx+c（a≠0）与y轴交于点C，与x轴交于点A(3，0)、B(﹣1，0)，则下列结论：①abc＞0，②b﹣2a＞0，③8a+c＞0，④a+b＞n（an+b）（n≠1）．其中正确的有．

查看试题解析

三、解答题

17. 解方程：x²+2x+1＝4．

查看试题解析
18. 如图，在Rt $△$ ABC中，∠ACB＝90°， $△$ EDC是 $△$ ABC绕着点C顺时针方向旋转90°得到的，若AB＝5，AC＝4，求BE的长．

查看试题解析
19. 如图，平面直角坐标系内，小正方形网格的边长为1个单位长度， $△$ ABC的三个顶点的坐标分别为A(2，5)，B(1，1)，C(4，3)．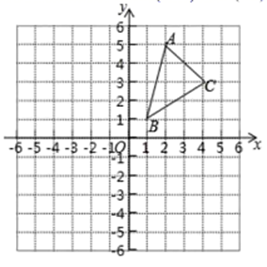

(1)、画出 $△$ ABC关于原点O成中心对称的图形 $△$ A₁B₁C₁ ．

(2)、求 $△$ A₁B₁C₁的面积．

查看试题解析
20. 已知关于x的方程x²+2mx+m²﹣1＝0．

(1)、不解方程，判别方程根的情况；

(2)、若方程有一个根为﹣1，求m的值．

查看试题解析
21. 如图是二次函数y＝ax²+bx+c（a≠0）图象的一部分，对称轴为直线x＝1，根据图象完成下列问题：

(1)、请补充完整二次函数对称轴直线x＝1左边的函数图象．

(2)、请写出三个正确的结论．

查看试题解析
22. 某农场要建一个面积为80m²的长方形养鸡场，鸡场的一边靠墙（墙AB长为15m），另外三边用木栏围成，木栏总长26m，求养鸡场CD边和DE边的长分别是多少？设养鸡场CD边的长为xm．

(1)、填空：养鸡场DE边的长为m（用含x的代数式表示）；

(2)、请你列出方程，求出问题的解．

查看试题解析
23. 在国庆期间，大润发商场新上市了一款童装，进价每件60元，现以每件100元销售，每天可售出20件．在试销售阶段发现，若每件童装降价1元，那么每天就可多售2件，设每件童装单价降价了x元．

(1)、若销售单价降低5元，则该款童装每天的销售量为件，每天利润是元；

(2)、请写出每天销售该款童装的利润y（元）与每件童装降价x（元）之间的函数关系式；

(3)、当每件童装销售单价定为多少元时，商场每天可获得最大利润？最大利润是多少元？

查看试题解析
24. 如图1，在 $△$ ABC中，CA＝CB，∠ACB＝90°，D是 $△$ ABC内部一点，∠ADC＝135°，将线段CD绕点C逆时针旋转90°，得到线段CE，连接DE．

(1)、求∠CDE的度数，并说明A、D、E三点是否共线；

(2)、在（1）的条件下，连接BE，如图2，过点C作CM⊥DE于点M，请判断线段AE，CM和BE之间的数量关系，并说明理由．

查看试题解析
25. 如图，直线y＝﹣ $\frac{1}{2}$ x+2与x轴交于点B，与y轴交于点C，已知二次函数的图象经过点B、C和点A(﹣1，0)．

(1)、求B、C两点的坐标；

(2)、求该二次函数的解析式；

(3)、若抛物线的对称轴与x轴交于点D，则在抛物线的对称轴上是否存在一点N，使 $△$ NCD为等腰三角形？若存在，求点N的坐标；若不存在，请说明理由．

查看试题解析