安徽省宣城市三县四校教学联盟2021-2022学年九年级上学期期中数学试题

试卷更新日期：2021-12-07 类型：期中考试

进入出卷网下载

一、单选题

1. 在下面的图形中，相似的一组是（）

A、 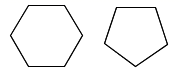B、 C、 D、

查看试题解析
2. 抛物线y＝﹣2x²＋1的顶点坐标是（）

A、（﹣2，0） B、（0，1） C、（0，﹣1） D、（﹣2，1）

查看试题解析
3. 若 $\frac{x}{y} = \frac{2}{3}$ ，则 $\frac{x + y}{y}$ 的值为（）

A、 $\frac{1}{3}$ B、﹣ $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{5}{3}$

查看试题解析
4. 下列各点中，在反比例函数y＝﹣ $\frac{4}{x}$ 图象上的是（）

A、（﹣1，4） B、（1，4） C、（﹣2，﹣2） D、（2，2）

查看试题解析
5. 某商场降价销售一批名牌球鞋，已知所获利润y（元）与降价金额x（元）之间满定函数关系式y＝﹣x²＋50x＋600，若降价10元，则获利为（）

A、800元 B、600元 C、1200元 D、1000元

查看试题解析
6. 若矩形ABCD∽矩形EFGH，相似比为2：3，已知AB＝4cm，BC＝5cm，则矩形EFGH的周长是（）

A、12cm B、27cm C、24cm D、18cm

查看试题解析
7. 中国古代在利用“计里画方”（比例缩放和直角坐标网格体系）的方法制作地图时，会利用测杆、水准仪和照板来测量距离．在如图所示的测量距离AB的示意图中，记照板“内芯”的高度为EF，观测者的眼睛（图中用点C表示）与BF在同一水平线上，则下列结论中，正确的是（）

A、 $\frac{E F}{A B} = \frac{C F}{F B}$ B、 $\frac{E F}{A B} = \frac{C F}{C B}$ C、 $\frac{C E}{C A} = \frac{C F}{F B}$ D、 $\frac{C E}{E A} = \frac{C F}{C B}$

查看试题解析
8. 二次函数y＝ax²＋bx＋c（abc≠0）的图象如图所示，反比例函数y＝ $\frac{c}{x}$ 与正比例函数y＝bx在同一坐标系内的大致图象是（）

A、 B、 C、 D、

查看试题解析
9. 如图，在△ABC中，∠A＝60°，AB＝4，AC＝6，将△ABC沿图示中的虚线剪开，有如下几种剪法，其中满足剪下的阴影三角形与△ABC相似的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，点C、A、M、N在同一条直线l上．其中， $△ A B C$ 是等腰直角三角形， $∠ B = 90 °$ ，四边形 $M N P Q$ 为正方形，且 $A C = 4 ， M N = 2$ ，将等腰 $R t △ A B C$ 沿直线l向右平移．若起始位置为点A与点M重合，终止位置为点C与点N重合．设点A平移的距离为x ，两个图形重叠部分的面积为y ，则y与x的函数图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 二次函数y＝ $\frac{1}{2}$ ${(3 - x)}^{2}$ 图象的开口向．

查看试题解析
12. 如果两个相似多边形面积的比为25：49，则它们的相似比为．

查看试题解析
13. 如图，已知一次函数y＝ax（a＜0）与反比例函数y＝ $\frac{k}{x}$ （x＜0）的图象相交于点A，过点A作AB⊥y轴，垂足为B，若△OAB的面积为4，则k的值为．

查看试题解析
14. 如图，在平行四边形ABCD中，AC，BD相交于点O，E是OA的中点，连接BE并延长交AD于点F．

(1)、 $\frac{F D}{A F}$ ＝．

(2)、若△AEF的面积为4，则平行四边形ABCD的面积为．

查看试题解析

三、解答题

15. 已知二次函数y＝x²﹣2x﹣1，在平面直角坐标系中画出它的图象，并写出它的顶点坐标．

查看试题解析
16. 已知反比例函数y＝ $\frac{2 - k}{x}$ 的图象经过点A（3，﹣2）．

(1)、求k的值．

(2)、点C（x₁ ， y₁），B（x₂ ， y₂）均在反比例函数y＝ $\frac{2 - k}{x}$ 的图象上，若0＜x₁＜x₂ ，直接写出y₁ ， y₂的大小关系．

查看试题解析
17. 如图，在△ABC中，点D、E分别在边AB，AC上，∠AED＝∠B，线段AG分别交线段DE，BC于点F，G．

(1)、求证：△AED∽△ABC．

(2)、若AG平分∠BAC，求证： $\frac{A D}{A C} = \frac{D F}{C G}$ ．

查看试题解析
18. 如图，在平面直角坐标系中，一次函数y＝ax＋b（a≠0）的图象分别交x轴，y轴于A，B两点，与反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象交于C，D两点，DE⊥轴于点E，点C的坐标为（6，﹣1），DE＝3

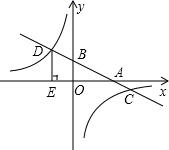(1)、求反比例函数与一次函数的表达式；

(2)、求△COD的面积．

查看试题解析
19. 如图，在四边形ABCD中，AD∥BC，∠BAD＝90°，且 $B D ⊥ D C$ ．

(1)、△ABD与△DCB相似吗？请说明理由；

(2)、若AD＝4，BC＝9，请求出BD的长．

查看试题解析
20. 如图，抛物线y＝ax²＋bx＋4（a≠0）与x轴交于A（﹣2，0），B（6，0）两点，与y轴交于点C，抛物线的对称轴l与x轴交于点M．

(1)、求抛物线的函数关系式．

(2)、设点P是直线l上的一个动点，求△PAC周长的最小值．

查看试题解析
21. 某“综合与实践”小组开展了测量本校旗杆高度的实践活动，他们制订了测量方案，并利用课余时间完成了实地测量．他们在旗杆底部所在的平地上，放置一个平面镜E来测量学校旗杆的高度，当镜子中心与旗杆的距离EB＝20米，镜子中心与测量者的距离ED＝2米时，测量者刚好从镜子中看到旗杆的顶端点A．已知测量者的身高为1.6米，测量者的眼睛距地面的高度为1.5米，求学校旗杆的高度是多少米．

(1)、在计算过程中C，D之间的距离应是米．

(2)、根据以上测量结果，请你帮助“综合与实践”小组求出学校旗杆AB的高度．

(3)、该“综合与实践”小组在定制方案时，讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案，但未被采纳．你认为其原因可能是什么？（写出一条即可）

查看试题解析
22. 某地种植某种水果，其成本经过测算为20元/kg，投放市场后，经过市场调研发现，这种水果在上市的一段时间内的销售单价p（元/kg）与时间t（天）之间的函数图象如图所示，且其日销售量y（kg）与时间t（天）的关系是y＝﹣2t＋120，天数为整数．

(1)、试求销售单价p（元/kg）与时间t（天）之间的函数关系式．

(2)、哪一天的销售利润最大？最大日销售利润为多少？

查看试题解析
23. 如图，将矩形纸片ABCD（AD＞DC）的∠A沿着过点D的直线折叠，使点A落在BC边上，落点为E，折痕交AB边于点F．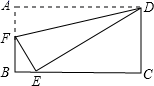

(1)、图中的全等三角形是，相似三角形是．

(2)、若BE：EC＝1：4，CD＝9，求BF的长；

(3)、若BE：EC＝m：n，求AF：FB．（用含有m，n的代数式表示）

查看试题解析