2022年苏科版初中数学《中考一轮复习》 专题三 函数 3.2 一次函数的图象与性质
试卷更新日期:2021-12-07 类型:一轮复习
一、单选题
-
1. 若正比例函数 的图象经过点 ,则 的值为( )A、 B、 C、 D、2. 在平面直角坐标系中,一次函数y=2x﹣5的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 已知一次函数 ( 为常数)的图象经过 , ,若 , ,则 的值可能是( )A、-1 B、0 C、1 D、24. 如果 , ,那么一次函数 的图象大致是( )A、
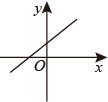 B、
B、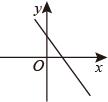 C、
C、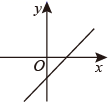 D、
D、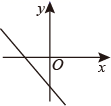 5. 如图,已知直线 过点 ,过点 的直线 交 轴于点 ,则关于的不等式组 的解集为( )
5. 如图,已知直线 过点 ,过点 的直线 交 轴于点 ,则关于的不等式组 的解集为( )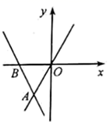 A、 B、 C、 D、6. 我们记函数 的最大值为 ,函数的最小值为 ,已知函数 的 ,且 ,则 的取值范围为( )A、 B、 C、 D、7. 已知一次函数y1=ax+b , y2=cx+d(a , b , c , d均为常数,且a•c≠0)在平面直角坐标系中的图象如图所示,则( )
A、 B、 C、 D、6. 我们记函数 的最大值为 ,函数的最小值为 ,已知函数 的 ,且 ,则 的取值范围为( )A、 B、 C、 D、7. 已知一次函数y1=ax+b , y2=cx+d(a , b , c , d均为常数,且a•c≠0)在平面直角坐标系中的图象如图所示,则( )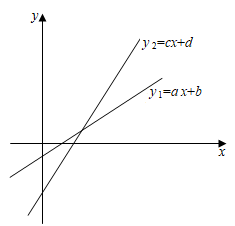 A、c<a<d<b B、a<c<d<b C、d<b<c<a D、d<b<a<c8. 如图,一次函数 与y轴相交于点 ,与 轴相交于点 ,在直线 上取一点 (点 不与 , 重合),过点 作 轴,垂足为点 ,连结 ,若 的面积恰好为 ,则满足条件的 点有( )
A、c<a<d<b B、a<c<d<b C、d<b<c<a D、d<b<a<c8. 如图,一次函数 与y轴相交于点 ,与 轴相交于点 ,在直线 上取一点 (点 不与 , 重合),过点 作 轴,垂足为点 ,连结 ,若 的面积恰好为 ,则满足条件的 点有( ) A、1个 B、2个 C、3个 D、4个9. 已知A、B、C三地顺次在同一直线上,甲、乙两人均骑车从A地出发,以同一路线向C地匀速行驶.甲比乙早出发5分钟,甲到达B地休息了2分钟后,乙追上了甲,接着,甲、乙同时从B地以各自的原速继续向C地行驶.当乙到达C地后,乙立即掉头并以原速的 按原路返回A地;而甲也立即以原速的 继续向C地行驶,到达C地就停止.若甲、乙之间的距离y(米)与甲出发的时间x(分)之间的函数关系如图所示,则下列说法错误的是( )
A、1个 B、2个 C、3个 D、4个9. 已知A、B、C三地顺次在同一直线上,甲、乙两人均骑车从A地出发,以同一路线向C地匀速行驶.甲比乙早出发5分钟,甲到达B地休息了2分钟后,乙追上了甲,接着,甲、乙同时从B地以各自的原速继续向C地行驶.当乙到达C地后,乙立即掉头并以原速的 按原路返回A地;而甲也立即以原速的 继续向C地行驶,到达C地就停止.若甲、乙之间的距离y(米)与甲出发的时间x(分)之间的函数关系如图所示,则下列说法错误的是( )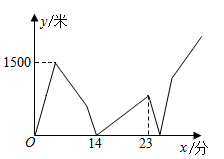 A、两地相距3600米 B、甲、乙两人在第24分钟时第二次相遇 C、甲从A地到C地共用时26分钟 D、当甲到达C地时,乙距B地2475米10. 甲、乙两工程队分别同时开挖两条600长的管道,所挖管道长度 (米)与挖掘时间 (天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖2天后,每天挖50米;③甲队比乙队提前3天完成任务;④当 或6时,甲、乙两队所挖管道长度都相差100米,正确的有( )
A、两地相距3600米 B、甲、乙两人在第24分钟时第二次相遇 C、甲从A地到C地共用时26分钟 D、当甲到达C地时,乙距B地2475米10. 甲、乙两工程队分别同时开挖两条600长的管道,所挖管道长度 (米)与挖掘时间 (天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖2天后,每天挖50米;③甲队比乙队提前3天完成任务;④当 或6时,甲、乙两队所挖管道长度都相差100米,正确的有( )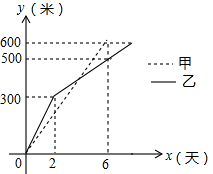 A、①②③ B、①②④ C、②③④ D、①③④
A、①②③ B、①②④ C、②③④ D、①③④二、填空题
-
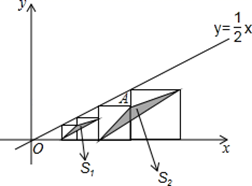
11. 直线 与 轴交点坐标为 .12. 一次函数y=kx﹣3k+1的图象必经过一个定点,该定点的坐标是13. 已知函数y= x﹣b与函数y= x﹣1的图象之间的距离等于3,则b的值为 .14. 若 是一次函数 图象上两个不同的点,且 ,则 .15. 函数y=(3-m)x+n(m,n为常数,m≠3),若2m+n=1,当-1≤x≤3时,函数有最大值2,则n= .16. 将一次函数 的图象绕原点O逆时针旋转 ,所得到的图像对应的函数表达式是.17. 在平面直角坐标系中,点P(x0 , y0)到直线Ax+By+C=0的距离公式为: ,则点P(3,-3)到直线 的距离为.18. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y= x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn , 则第4个正方形的边长及S3的值分别为 .
三、解答题
-
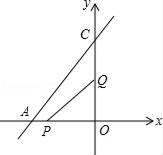
19. 已知y=y1+y2 , 其中y1与x﹣3成正比例,y2与x2+1成正比例,且当x=0时,y=﹣4,当x=﹣1时,y=﹣6.(1)、求y与x的函数关系式;(2)、判断点A(1,﹣4)是否在此函数图象上,并说明理由.20. 如图已知直线AC的函数解析式为y= x+8,点P从点A开始沿AO方向以1个单位/秒的速度运动,点Q从O点开始沿OC方向以2个单位/秒的速度运动.如果P、Q两点分别从点A、点O同时出发,经过多少秒后能使△POQ的面积为8个平方单位?
 21. 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
21. 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
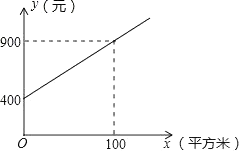 (1)、求如图所示的y与x的函数表达式;
(1)、求如图所示的y与x的函数表达式;
(2)、如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
22. 如图,直线 与直线 交于点M(﹣1,2),与 轴分别交于点A,B,与 轴分别交于C,D.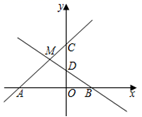 (1)、根据图像写出方程组 的解是 .(2)、根据函数图象写出不等式 的解集 .(3)、求直线AC,直线BD与 轴围成的△ABM的面积.23. 如图,有 号、 号两个探测气球同时出发且匀速上升, 号气球从海拔5m处出发,以1m/min的速度上升.与此同时, 号探测气球从海拔15m处出发,以0.5m/min的速度上升.设气球上升时间为xmin.
(1)、根据图像写出方程组 的解是 .(2)、根据函数图象写出不等式 的解集 .(3)、求直线AC,直线BD与 轴围成的△ABM的面积.23. 如图,有 号、 号两个探测气球同时出发且匀速上升, 号气球从海拔5m处出发,以1m/min的速度上升.与此同时, 号探测气球从海拔15m处出发,以0.5m/min的速度上升.设气球上升时间为xmin.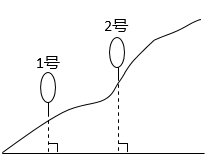 (1)、分别直接写出 号气球的海拔高度 (单位:m)、 号气球的海拔高度 (单位:m)与 (单位: )的函数关系式;(不必写出 的取值范围)(2)、气球上升多少分钟时,两个气球位于同一高度?(3)、气球上升多少分钟时,两个气球所在位置的海拔高度相差5m?24. 小张骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶,他距乙地的距离y(km)与时间x(h)的关系如图中折线所示,小李开车匀速从乙地到甲地,比小张晚出发一段时间,他距乙地的距离y(km)与时间x(h)的关系如图中线段AB所示.
(1)、分别直接写出 号气球的海拔高度 (单位:m)、 号气球的海拔高度 (单位:m)与 (单位: )的函数关系式;(不必写出 的取值范围)(2)、气球上升多少分钟时,两个气球位于同一高度?(3)、气球上升多少分钟时,两个气球所在位置的海拔高度相差5m?24. 小张骑自行车匀速从甲地到乙地,在途中休息了一段时间后,仍按原速行驶,他距乙地的距离y(km)与时间x(h)的关系如图中折线所示,小李开车匀速从乙地到甲地,比小张晚出发一段时间,他距乙地的距离y(km)与时间x(h)的关系如图中线段AB所示. (1)、小李到达甲地后,再经过小时小张也到达乙地;小张骑自行车的速度是千米/小时.(2)、小张出发几小时与小李相距15千米?(3)、若小李想在小张休息期间与他相遇,则他出发的时间x应在什么范围?(直接写出答案)25. 某通讯公司就手机流量套餐推出三种方案,如下表:
(1)、小李到达甲地后,再经过小时小张也到达乙地;小张骑自行车的速度是千米/小时.(2)、小张出发几小时与小李相距15千米?(3)、若小李想在小张休息期间与他相遇,则他出发的时间x应在什么范围?(直接写出答案)25. 某通讯公司就手机流量套餐推出三种方案,如下表:A方案
B方案
C方案
每月基本费用(元)
20
56
266
每月免费使用流量(兆)
1024
m
无限
超出后每兆收费(元)
n
n
A,B,C三种方案每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系如图所示.
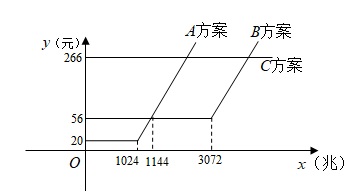 (1)、请直接写出m,n的值.(2)、在A方案中,当每月使用的流量不少于1024兆时,求每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系式.(3)、在这三种方案中,当每月使用的流量超过多少兆时,选择C方案最划算?26. 为了切实保护汉江生态环境,襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后,某水库自然生态养殖的鱼在市场上热销,经销商老李每天从该水库购进草鱼和鲢鱼进行销售,两种鱼的进价和售价如下表所示:
(1)、请直接写出m,n的值.(2)、在A方案中,当每月使用的流量不少于1024兆时,求每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系式.(3)、在这三种方案中,当每月使用的流量超过多少兆时,选择C方案最划算?26. 为了切实保护汉江生态环境,襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后,某水库自然生态养殖的鱼在市场上热销,经销商老李每天从该水库购进草鱼和鲢鱼进行销售,两种鱼的进价和售价如下表所示:进价(元/斤)
售价(元/斤)
鲢鱼
5
草鱼
销量不超过200斤的部分
销量超过200斤的部分
8
7
已知老李购进10斤鲢鱼和20斤草鱼需要155元,购进20斤鲢鱼和10斤草鱼需要130元.
(1)、求 , 的值;(2)、老李每天购进两种鱼共300斤,并在当天都销售完,其中销售鲢鱼不少于80斤且不超过120斤,设每天销售鲢鱼 斤(销售过程中损耗不计).①分别求出每天销售鲢鱼获利 (元),销售草鱼获利 (元)与 的函数关系式,并写出 的取值范围;
②端午节这天,老李让利销售,将鲢鱼售价每斤降低 元,草鱼售价全部定为7元斤,为了保证当天销售这两种鱼总获利 (元)的最小值不少于320元,求 的最大值.
27. 2020年5月16日,“钱塘江诗路”航道全线开通,一艘游轮从杭州出发前往衢州,线路如图1所示.当游轮到达建德境内的“七里扬帆”景点时,一艘货轮沿着同样的线路从杭州出发前往衢州.已知游轮的速度为20km/h,游轮行驶的时间记为t(h),两艘轮船距离杭州的路程s(km)关于t(h)的图象如图2所示(游轮在停靠前后的行驶速度不变). (1)、写出图2中C点横坐标的实际意义,并求出游轮在“七里扬帆”停靠的时长.(2)、若货轮比游轮早36分钟到达衢州.问:
(1)、写出图2中C点横坐标的实际意义,并求出游轮在“七里扬帆”停靠的时长.(2)、若货轮比游轮早36分钟到达衢州.问:①货轮出发后几小时追上游轮?
②游轮与货轮何时相距12km?
28. 在平面直角坐标系中, 为坐标原点直线 与 轴交于点 ,与 轴交于点 , , 的面积为2.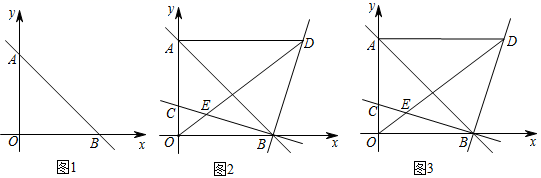 (1)、如图1,求直线 的解析式;(2)、如图2,线段 上有一点 ,直线 为 , 轴,将 绕点 顺时针旋转 ,交 于点 ,求点 的坐标.(用含 的式子表示)(3)、如图3,在(2)的条件下,连接 ,交直线 于点 ,若 ,求点 的坐标.
(1)、如图1,求直线 的解析式;(2)、如图2,线段 上有一点 ,直线 为 , 轴,将 绕点 顺时针旋转 ,交 于点 ,求点 的坐标.(用含 的式子表示)(3)、如图3,在(2)的条件下,连接 ,交直线 于点 ,若 ,求点 的坐标.