2021-2022学年北师版数学八年级上册期末模拟试题二
试卷更新日期:2021-12-06 类型:期末考试
一、单选题
-
1. 在平面直角坐标系 中,点 关于 轴对称的点 的坐标是( )A、 B、 C、 D、2. 今年是三年禁毒“大扫除”攻坚克难之年.为了让学生认识毒品的危害,某校举办了禁毒知识比赛,小红所在班级学生的平均成绩是80分,小星所在班级学生的平均成绩是85分,在不知道小红和小星成绩的情况下,下列说法比较合理的是( )A、小红的分数比小星的分数低 B、小红的分数比小星的分数高 C、小红的分数与小星的分数相同 D、小红的分数可能比小星的分数高3. 我国古代数学古典名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”其大意是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量,木条还剩余1尺;问长木多少尺?如果设木条长为x尺,绳子长为y尺,则下面所列方程组正确的是( )A、 B、 C、 D、4. 如图,将一副三角板在平行四边形ABCD中作如下摆放,设 ,那么 ( )
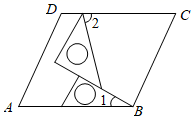 A、 B、 C、 D、5. 实数 在数轴上的对应点可能是( )
A、 B、 C、 D、5. 实数 在数轴上的对应点可能是( ) A、 点 B、 点 C、 点 D、 点6. 计算: ( )A、0 B、1 C、2 D、7. 如图,从一个大正方形中截去面积为 和 的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为( )
A、 点 B、 点 C、 点 D、 点6. 计算: ( )A、0 B、1 C、2 D、7. 如图,从一个大正方形中截去面积为 和 的两个小正方形,若随机向大正方形内投一粒米,则米粒落在图中阴影部分的概率为( )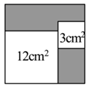 A、 B、 C、 D、8. 下列计算正确的是( )A、 B、 C、 D、9. 如图,一束水平光线照在有一定倾斜角度的平面镜上,若入射光线与出射光线的夹角为60°,则平面镜的垂线与水平地面的夹角α的度数是( )
A、 B、 C、 D、8. 下列计算正确的是( )A、 B、 C、 D、9. 如图,一束水平光线照在有一定倾斜角度的平面镜上,若入射光线与出射光线的夹角为60°,则平面镜的垂线与水平地面的夹角α的度数是( )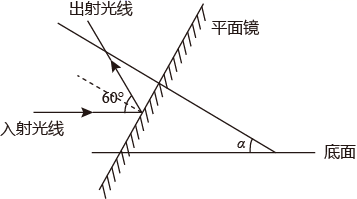 A、15° B、30° C、45° D、60°10. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、
A、15° B、30° C、45° D、60°10. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、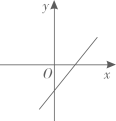 B、
B、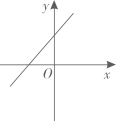 C、
C、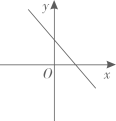 D、
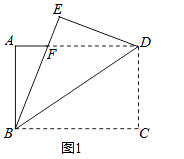
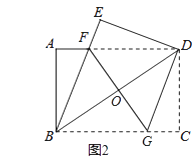
D、 11. 鄂尔多斯动物园内的一段线路如图1所示,动物园内有免费的班车,从入口处出发,沿该线路开往大象馆,途中停靠花鸟馆(上下车时间忽略不计),第一班车上午9:20发车,以后每隔10分钟有一班车从入口处发车,且每一班车速度均相同.小聪周末到动物园游玩,上午9点到达入口处,因还没到班车发车时间,于是从入口处出发,沿该线路步行25分钟后到达花鸟馆,离入口处的路程y(米)与时间x(分)的函数关系如图2所示,下列结论错误的是( )
11. 鄂尔多斯动物园内的一段线路如图1所示,动物园内有免费的班车,从入口处出发,沿该线路开往大象馆,途中停靠花鸟馆(上下车时间忽略不计),第一班车上午9:20发车,以后每隔10分钟有一班车从入口处发车,且每一班车速度均相同.小聪周末到动物园游玩,上午9点到达入口处,因还没到班车发车时间,于是从入口处出发,沿该线路步行25分钟后到达花鸟馆,离入口处的路程y(米)与时间x(分)的函数关系如图2所示,下列结论错误的是( )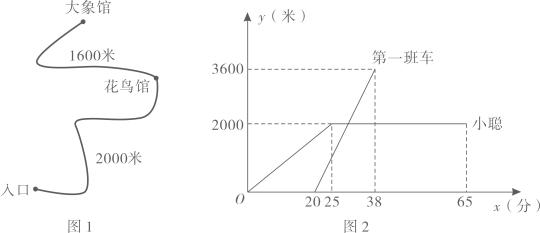 A、第一班车离入口处的距离y(米)与时间x(分)的解析式为y=200x﹣4000(20≤x≤38) B、第一班车从入口处到达花鸟馆所需的时间为10分钟 C、小聪在花鸟馆游玩40分钟后,想坐班车到大象馆,则小聪最早能够坐上第四班车 D、小聪在花鸟馆游玩40分钟后,如果坐第五班车到大象馆,那么比他在花鸟馆游玩结束后立即步行到大象馆提前了7分钟(假设小聪步行速度不变)12. 我市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入两工程队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米?设甲工程队每天施工 米,乙工程队每天施工 米,根据题意,所列方程组正确的是( )A、 B、 C、 D、
A、第一班车离入口处的距离y(米)与时间x(分)的解析式为y=200x﹣4000(20≤x≤38) B、第一班车从入口处到达花鸟馆所需的时间为10分钟 C、小聪在花鸟馆游玩40分钟后,想坐班车到大象馆,则小聪最早能够坐上第四班车 D、小聪在花鸟馆游玩40分钟后,如果坐第五班车到大象馆,那么比他在花鸟馆游玩结束后立即步行到大象馆提前了7分钟(假设小聪步行速度不变)12. 我市在落实国家“精准扶贫”政策的过程中,为某村修建一条长为400米的公路,由甲、乙两个工程队负责施工.甲工程队独立施工2天后,乙工程队加入两工程队联合施工3天后,还剩50米的工程.已知甲工程队每天比乙工程队多施工2米,求甲、乙工程队每天各施工多少米?设甲工程队每天施工 米,乙工程队每天施工 米,根据题意,所列方程组正确的是( )A、 B、 C、 D、二、填空题
-
13. 将直线 向左平移 ( )个单位后,经过点(1,−3),则 的值为.14. 以水平数轴的原点 为圆心过正半轴 上的每一刻度点画同心圆,将 逆时针依次旋转 、 、 、 、 得到 条射线,构成如图所示的“圆”坐标系,点 、 的坐标分别表示为 、 ,则点 的坐标表示为.
 15. 已知x、y满足方程组 ,则 的值为.16. 观察下列等式: ;
15. 已知x、y满足方程组 ,则 的值为.16. 观察下列等式: ;;
;
……
根据以上规律,计算 .
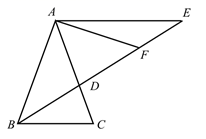
17. 在直角坐标系中,点A1从原点出发,沿如图所示的方向运动,到达位置的坐标依次为:A2(1,0),A3(1,1),A4(﹣1,1),A5(﹣1,﹣1),A6(2,﹣1),A7(2,2),….若到达终点An(506,﹣505),则n的值为 . 18. 如图,在正方形 ABCD ,E是对角线 BD 上一点, AE 的延长线交 CD 于点F , 连接 CE .若∠BAE=56° ,则 ∠CEF= ° .
18. 如图,在正方形 ABCD ,E是对角线 BD 上一点, AE 的延长线交 CD 于点F , 连接 CE .若∠BAE=56° ,则 ∠CEF= ° .
三、解答题
-
19. 计算:20. 计算:﹣ ÷(2 )21. 解方程组:(1)、(2)、(3)、22. 某校要从甲,乙两名学生中挑选一名学生参加数学竞赛,在最近的8次选拔赛中,他们的成绩(成绩均为整数,单位:分)如下:
甲:92,95,96,88,92,98,99,100
乙:100,87,92,93,9▆,95,97,98
由于保存不当,学生乙有一次成绩的个位数字模糊不清,
(1)、求甲成绩的平均数和中位数;(2)、求事件“甲成绩的平均数大于乙成绩的平均数”的概率;(3)、当甲成绩的平均数与乙成绩的平均数相等时,请用方差大小说明应选哪个学生参加数学竞赛.23. 某通讯公司就手机流量套餐推出三种方案,如下表:A方案
B方案
C方案
每月基本费用(元)
20
56
266
每月免费使用流量(兆)
1024
m
无限
超出后每兆收费(元)
n
n
A,B,C三种方案每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系如图所示.
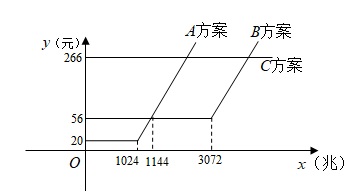 (1)、请直接写出m,n的值.(2)、在A方案中,当每月使用的流量不少于1024兆时,求每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系式.(3)、在这三种方案中,当每月使用的流量超过多少兆时,选择C方案最划算?24. 为了切实保护汉江生态环境,襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后,某水库自然生态养殖的鱼在市场上热销,经销商老李每天从该水库购进草鱼和鲢鱼进行销售,两种鱼的进价和售价如下表所示:
(1)、请直接写出m,n的值.(2)、在A方案中,当每月使用的流量不少于1024兆时,求每月所需的费用y(元)与每月使用的流量x(兆)之间的函数关系式.(3)、在这三种方案中,当每月使用的流量超过多少兆时,选择C方案最划算?24. 为了切实保护汉江生态环境,襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后,某水库自然生态养殖的鱼在市场上热销,经销商老李每天从该水库购进草鱼和鲢鱼进行销售,两种鱼的进价和售价如下表所示:进价(元/斤)
售价(元/斤)
鲢鱼
5
草鱼
销量不超过200斤的部分
销量超过200斤的部分
8
7
已知老李购进10斤鲢鱼和20斤草鱼需要155元,购进20斤鲢鱼和10斤草鱼需要130元.
(1)、求 , 的值;(2)、老李每天购进两种鱼共300斤,并在当天都销售完,其中销售鲢鱼不少于80斤且不超过120斤,设每天销售鲢鱼 斤(销售过程中损耗不计).①分别求出每天销售鲢鱼获利 (元),销售草鱼获利 (元)与 的函数关系式,并写出 的取值范围;
②端午节这天,老李让利销售,将鲢鱼售价每斤降低 元,草鱼售价全部定为7元斤,为了保证当天销售这两种鱼总获利 (元)的最小值不少于320元,求 的最大值.