2021-2022学年浙江省台州市七年级第一学期期末模拟试卷

试卷更新日期：2021-12-06 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣2021的倒数是（）

A、2021 B、 $\frac{1}{2021}$ C、﹣2021 D、 $- \frac{1}{2021}$

查看试题解析
2. 已知地球上海洋面积为316000000km² ， 316000000这个数用科学记数法可表示为（）

A、3.16×10⁹ B、3.16×10⁸ C、3.16×10⁷ D、3.16×10⁶

查看试题解析
3. 计算 (-1)＋(+2) 的值为（）

A、3 B、-3 C、-1 D、1

查看试题解析
4. 单项式﹣2xy³的次数是（）

A、2 B、3 C、4 D、5

查看试题解析
5. 某工厂2021年数字化改造总投入 $100$ 万元，2023年总投入预计达到 $180$ 万元，设年平均增长率为 $x$ ，则可列方程为（）

A、 $100 (1 + x) = 180$ B、 $100 (1 + 2 x) = 180$ C、 $100 (1 + x + x^{2}) = 180$ D、 $100 {(1 + x)}^{2} = 180$

查看试题解析
6. 下列说法正确的是（）

A、单项式 $\frac{3}{2} π x^{2} y$ 的系数是 $\frac{3}{2}$ B、若AB＝BC，则点B是线段AC的中点 C、3和5是同类项 D、连接两点的线段就是两点间的距离

查看试题解析
7. 如图，是一个正方体纸盒的展开图，若在其中的三个正方形A ， B ， C内分别填入适当的数，使得它们折成正方体后相对面上的两个数互为相反数，则填入正方形A ， B ， C内的三个数依次为（）

A、1，－2，0 B、0，－2，1 C、－2，0，1 D、－2，1，0

查看试题解析
8. 将方程 $\frac{2 x - 1}{3} - \frac{x + 1}{2} = 1$ 去分母得到 $2 (2 x - 1) - 3 x + 1 = 6$ ，错在（）

A、分母的最小公倍数找错 B、去分母时漏乘项 C、去分母时分子部分没有加括号 D、去分母时各项所乘的数不同

查看试题解析
9. 若“！”是一种数学运算符号，并且1!=1， 2!=2 $\times$ 1=2， 3!=3 $\times$ 2 $\times$ 1=6，……，则 $\frac{100 ！}{98 ！}$ 的值为（）

A、 $\frac{100}{98}$ B、99！ C、9900 D、 2！

查看试题解析
10. 如图所示，圆的周长为4个单位长度在圆周的4等分点处标上字母A，B，C，D，先将圆周上的字母A对应的点与数轴上的原点重合，再将圆沿着数轴向右滚动，那么数轴上的1949所对应的点与圆周上字母 $($ $)$ 所对应的点重合.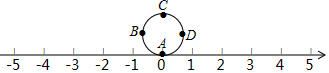

A、A B、B C、C D、D

查看试题解析

二、填空题

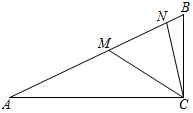
11. —2022的绝对值是.

查看试题解析
12. 单项式 $- \frac{1}{2} π a^{2} b^{3}$ 的系数为．

查看试题解析
13. 已知方程 $2 x - 4 = 0$ ，则 $x =$ .

查看试题解析
14. 如图，在△ABC中，∠ACB＝90°，AC＝12，BC＝5，AN＝AC，BM＝BC，则MN的长为.

查看试题解析
15. 若 $∠ A = 30 ° 1 8^{'}$ ，则 $∠ A$ 的余角是.

查看试题解析
16. 据统计，2021年第一季度宜宾市实现地区生产总值约652亿元，若使该市第三季度实现地区生产总值960亿元，设该市第二、三季度地区生产总值平均增长率为x，则可列方程.

查看试题解析
17. 已知对于非零的两个实数 $a$ 、 $b$ ，规定 $a \oplus b = b - \frac{2}{a}$ ，若 $1 \oplus (x + 1) = 1$ ，则 $x$ 的值为．

查看试题解析

三、作图题

18. 如图，平面上有四个点A、B、C、D，根据下列语句画图.

（ 1 ）画直线AB；

（ 2 ）作射线BC；

（ 3 ）画线段BD；

（ 4 ）连接AC交BD于点E.

查看试题解析

四、计算题

19. 计算

(1)、 ${(- \frac{1}{2})}^{- 2} + \sqrt[3]{8} - | 1 - \sqrt{9} |$ .

(2)、 $2 b^{2} + (a + b) (a - b) - {(a - b)}^{2}$ .

查看试题解析
20. 解方程： $3 x - 8 = x + 2$ .

查看试题解析
21. 先化简，再求值： $\frac{1}{2}$ x-2（x- $\frac{1}{3}$ y²）+（- $\frac{3}{2} x + \frac{1}{3} y^{2}$ ），其中x=-2，y= $\frac{2}{3}$ ．

查看试题解析

五、综合题

22. 在日历牌上，我们可以发现一些日期数满足一定的规律.如图是今年4月的日历牌，若任意选择图中上下相邻的四个日期（阴影部分），将其中四个位置上的数交叉相乘，再相减，例如： $3 \times 9 - 2 \times 10 = 7 ， 6 \times 12 - 5 \times 13 = 7$ ，不难发现，结果都是7

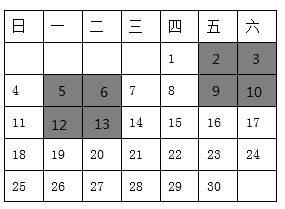(1)、请再选择两个类似的部分试一试，看看是否符合这个规律

(2)、设符合条件的四个日期左上角位置上的数为a，请利用整式的运算对以上的规律加以证明.

查看试题解析
23. 如图，直线AB，CD相交于点O，OD平分∠BOE，OF平分∠AOE

(1)、判断OF与OD的位置关系，并进行证明.

(2)、若∠AOC：∠AOD＝1：5，求∠EOF的度数.

查看试题解析
24. 某文艺团体为“希望工程”募捐组织了一场义演，共售出1000张票，筹出票款6920元，且每张成人票8元，学生票5元.

(1)、问成人票与学生票各售出多少张？

(2)、若票价不变，仍售出1000张票，所得的票款可能是7290元吗？为什么？

查看试题解析
25. 如图，在数轴上点A表示的有理数为 $- 6$ ，点B表示的有理数为6．点P从点A出发以每秒2个单位长度的速度由 $A \to B \to A$ 运动，同时，点Q从点P出发以每秒1个单位长度的速度由 $B \to A$ 运动，当点Q到达点A时 $P ， Q$ 两点停止运动，设运动时间为t(单位：秒)．

(1)、求 $t = 2$ 时，求点P和点Q表示的有理数；

(2)、求点P与点Q第一次重合时的t值；

(3)、当t的值为多少时，点P表示的有理数与点Q表示的有理数距离是3个单位长度．

查看试题解析