2021-2022学年北师版数学九年级上册期末模拟试题二
试卷更新日期:2021-12-06 类型:期末考试
一、单选题
-
1. 如图是由6个相同的小立方体堆成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是( )
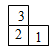 A、
A、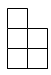 B、
B、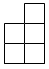 C、
C、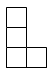 D、
D、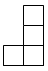 2. 小明计划到永州市体验民俗文化,想从“零陵渔鼓、瑶族长鼓舞、东安武术、舜帝祭典”四种民俗文化中任意选择两项,则小明选择体验“瑶族长鼓舞、舜帝祭典”的概率为( )A、 B、 C、 D、3. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )
2. 小明计划到永州市体验民俗文化,想从“零陵渔鼓、瑶族长鼓舞、东安武术、舜帝祭典”四种民俗文化中任意选择两项,则小明选择体验“瑶族长鼓舞、舜帝祭典”的概率为( )A、 B、 C、 D、3. 如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长是( )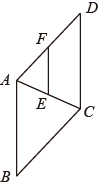 A、11 B、22 C、33 D、444. 如图,在矩形纸片ABCD中, , ,M是BC上的点,且 .将矩形纸片ABCD沿过点M的直线折叠,使点D落在AB上的点P处,点C落在点 处,折痕为MN,则线段PA的长是( )
A、11 B、22 C、33 D、444. 如图,在矩形纸片ABCD中, , ,M是BC上的点,且 .将矩形纸片ABCD沿过点M的直线折叠,使点D落在AB上的点P处,点C落在点 处,折痕为MN,则线段PA的长是( ) A、4 B、5 C、6 D、5. 已知反比例函数 的图象与正比例函数 的图象相交于 两点,若点 的坐标是 ,则点 的坐标是( )A、 B、 C、 D、6. 如图,在平面直角坐标系中, , , , ,将四边形 向左平移 个单位后,点 恰好和原点 重合,则 的值是( )
A、4 B、5 C、6 D、5. 已知反比例函数 的图象与正比例函数 的图象相交于 两点,若点 的坐标是 ,则点 的坐标是( )A、 B、 C、 D、6. 如图,在平面直角坐标系中, , , , ,将四边形 向左平移 个单位后,点 恰好和原点 重合,则 的值是( ) A、11.4 B、11.6 C、12.4 D、12.67. 已知关于x的一元二次方程x2-kx+k-3=0的两个实数根分别为 ,且 ,则k的值是( )A、-2 B、2 C、-1 D、18. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( )
A、11.4 B、11.6 C、12.4 D、12.67. 已知关于x的一元二次方程x2-kx+k-3=0的两个实数根分别为 ,且 ,则k的值是( )A、-2 B、2 C、-1 D、18. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( ) A、2 B、4 C、6 D、89. 如图,菱形 的顶点分别在反比例函数 和 的图象上,若 ,则 的值为( )
A、2 B、4 C、6 D、89. 如图,菱形 的顶点分别在反比例函数 和 的图象上,若 ,则 的值为( )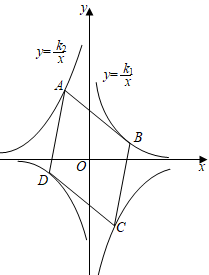 A、 B、 C、 D、10. 如图,在矩形纸片ABCD中,点E、F分别在矩形的边AB、AD上,将矩形纸片沿CE、CF折叠,点B落在H处,点D落在G处,点C、H、G恰好在同一直线上,若AB=6,AD=4,BE=2,则DF的长是( )
A、 B、 C、 D、10. 如图,在矩形纸片ABCD中,点E、F分别在矩形的边AB、AD上,将矩形纸片沿CE、CF折叠,点B落在H处,点D落在G处,点C、H、G恰好在同一直线上,若AB=6,AD=4,BE=2,则DF的长是( ) A、2 B、 C、 D、311. 平面直角坐标系 中,直线 与双曲线 相交于A,B两点,其中点A在第一象限.设 为双曲线 上一点,直线 , 分别交y轴于C,D两点,则 的值为( )A、2 B、4 C、6 D、812. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( )
A、2 B、 C、 D、311. 平面直角坐标系 中,直线 与双曲线 相交于A,B两点,其中点A在第一象限.设 为双曲线 上一点,直线 , 分别交y轴于C,D两点,则 的值为( )A、2 B、4 C、6 D、812. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( ) A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
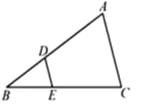
13. 如图,在 中,点 分别在边 上,且 , 与四边形 的面积的比为.
 14. 如图,点 分别在函数 的图象上,点 在 轴上.若四边形 为正方形,点 在第一象限,则 的坐标是.
14. 如图,点 分别在函数 的图象上,点 在 轴上.若四边形 为正方形,点 在第一象限,则 的坐标是.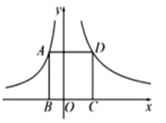 15. 若m,n是一元二次方程 的两个实数根,则 的值为.16. 如图,在菱形ABCD中, , ,Q为AB的中点,P为对角线BD上的任意一点,则 的最小值为.
15. 若m,n是一元二次方程 的两个实数根,则 的值为.16. 如图,在菱形ABCD中, , ,Q为AB的中点,P为对角线BD上的任意一点,则 的最小值为. 17. 如图,直线 与反比例函数 的图象交于A,B两点,与x轴交于点C,且 ,连接OA.已知 的面积为12,则k的值为.
17. 如图,直线 与反比例函数 的图象交于A,B两点,与x轴交于点C,且 ,连接OA.已知 的面积为12,则k的值为.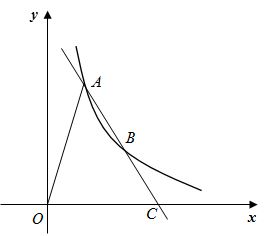 18. 如图,在菱形ABCD中,∠BAD=120°,交CD于点G.FH⊥CD于点H,连结CF.有下列结论:①AF=CF2=EF•FG;③FG:EG=4:5;④cos∠GFH= .
18. 如图,在菱形ABCD中,∠BAD=120°,交CD于点G.FH⊥CD于点H,连结CF.有下列结论:①AF=CF2=EF•FG;③FG:EG=4:5;④cos∠GFH= .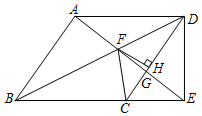
三、解答题
-
19. 目前,全国各地正在有序推进新冠疫苗接种工作.某单位为了解职工对疫苗接种的关注度,随机抽取了部分职工进行问卷调查(实时关注)、B(关注较多)、C(关注较少)(不关注)四类,现将调查结果绘制成如图所示的统计图.
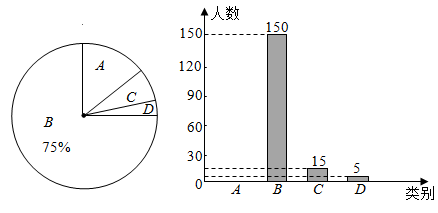
请根据图中信息,解答下列问题:
(1)、求C类职工所对应扇形的圆心角度数,并补全条形统计图;(2)、若D类职工中有3名女士和2名男士,现从中任意抽取2人进行随访,请用树状图或列表法求出恰好抽到一名女士和一名男士的概率.20. 如图,在 中,G为BC边上一点, ,延长DG交AB的延长线于点E , 过点A作 交CD的延长线于点F . 求证:四边形AEDF是菱形.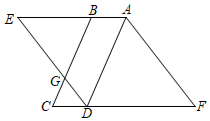 21. 如图,已知直线y=kx+b(k≠0)与双曲线y= 相较于A(m,3)、B(3,n)两点.
21. 如图,已知直线y=kx+b(k≠0)与双曲线y= 相较于A(m,3)、B(3,n)两点. (1)、求直线AB的解析式;(2)、连结AO并延长交双曲线于点C,连结BC交x轴于点D,连结AD,求△ABD的面积.22. 如图, 为等腰直角三角形,延长 至点B使 ,其对角线 , 交于点E.
(1)、求直线AB的解析式;(2)、连结AO并延长交双曲线于点C,连结BC交x轴于点D,连结AD,求△ABD的面积.22. 如图, 为等腰直角三角形,延长 至点B使 ,其对角线 , 交于点E. (1)、求证: ;(2)、求 的值.23. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?24. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .
(1)、求证: ;(2)、求 的值.23. 直播购物逐渐走进了人们的生活.某电商在抖音上对一款成本价为40元的小商品进行直播销售,如果按每件60元销售,每天可卖出20件.通过市场调查发现,每件小商品售价每降低5元,日销售量增加10件.(1)、若日利润保持不变,商家想尽快销售完该款商品,每件售价应定为多少元?(2)、小明的线下实体商店也销售同款小商品,标价为每件62.5元.为提高市场竞争力,促进线下销售,小明决定对该商品实行打折销售,使其销售价格不超过(1)中的售价,则该商品至少需打几折销售?24. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .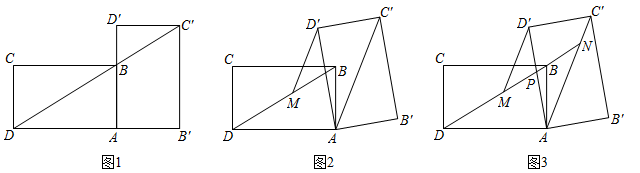
[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M . 线段D′M与DM相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P , N(如图3),发现线段DN , MN , PN存在一定的数量关系,请写出这个关系式,并加以证明.
25. 已知在 ABC中,O为BC边的中点,连接AO,将 AOC绕点O顺时针方向旋转(旋转角为钝角),得到 EOF,连接AE,CF.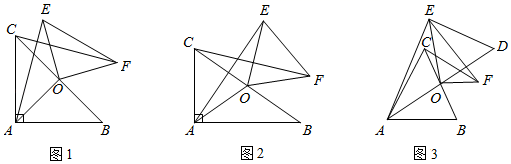 (1)、如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是;(2)、如图2,当∠BAC=90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、如图3,延长AO到点D,使OD=OA,连接DE,当AO=CF=5,BC=6时,求DE的长.
(1)、如图1,当∠BAC=90°且AB=AC时,则AE与CF满足的数量关系是;(2)、如图2,当∠BAC=90°且AB≠AC时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)、如图3,延长AO到点D,使OD=OA,连接DE,当AO=CF=5,BC=6时,求DE的长.