2022年苏科版初中数学《中考一轮复习》 专题三 函数 3.1 平面直角坐标系
试卷更新日期:2021-12-06 类型:一轮复习
一、单选题
-
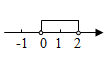
1. 在平面直角坐标系中,第四象限内有一点M,它到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )A、(-4,5) B、(-5,4) C、(4,-5) D、(5,-4)2. 已知点P(m+2,2m 4)在y轴上,则点P的坐标是( )A、(8,0) B、(0,8) C、(-8,0) D、(0,-8)3. 在平面直角坐标系中,将点A(-1,2)向下平移3个单位长度,再向右平移2个单位长度,得到点A′,则点A′的坐标是( )A、(-3,-1) B、(1,-1) C、(-1,1) D、(-4,4)4. 在平面直角坐标系中,已知点 在第二象限,则点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 已知点 关于原点对称的点在第二象限,则a的取值范围在数轴上表示( )A、
 B、
B、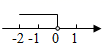 C、
C、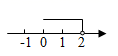 D、
D、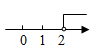 6. 如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(﹣1,1),(﹣3,1),(﹣1,﹣1),30秒后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )
6. 如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(﹣1,1),(﹣3,1),(﹣1,﹣1),30秒后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )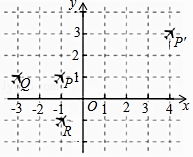 A、Q′(2,3),R′(4,1) B、Q′(2,3),R′(2,1) C、Q′(2,2),R′(4,1) D、Q′(3,3),R′(3,1)7. 在直角坐标平面内的机器人接受指令“[a,A]”(a≥0,0°<A<180°)后的行动结果为:在原地顺时针旋转A后,再向正前方沿直线行走a个单位长度.若机器人的位置在原点,正前方为y轴的负半轴,则它完成一次指令[2,60°]后位置的坐标为( )
A、Q′(2,3),R′(4,1) B、Q′(2,3),R′(2,1) C、Q′(2,2),R′(4,1) D、Q′(3,3),R′(3,1)7. 在直角坐标平面内的机器人接受指令“[a,A]”(a≥0,0°<A<180°)后的行动结果为:在原地顺时针旋转A后,再向正前方沿直线行走a个单位长度.若机器人的位置在原点,正前方为y轴的负半轴,则它完成一次指令[2,60°]后位置的坐标为( )
A、(-1,) B、(-1,-) C、(- , -1) D、(- , 1)8. 平面直角坐标系xOy中,已知A(﹣1,0)、B(3,0)、C(0,﹣1)三点,D(1,m)是一个动点,当△ACD的周长最小时,△ABD的面积为( )A、 B、 C、 D、9. 在平面直角坐标系中,点A(a,0),点B(2﹣a,0),且A在B的左边,点C(1,﹣1),连接AC,BC,若在AB,BC,AC所围成区域内(含边界),横坐标和纵坐标都为整数的点的个数为4个,那么a的取值范围为( )A、﹣1<a≤0 B、0≤a<1 C、﹣1<a<1 D、﹣2<a<210. 如图,已致点 的坐标为 ,点 在 轴的正半轴上,且 .过点 作 ,交 轴于点 ;过点 作 ,交 轴于点 ;过点 作 ,交 轴于点 ;……;按此规律进行下去,则点 的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 点 到x轴距离为.12. 若点P(1,n),Q(m,2),且PQ∥x轴,PQ=3,则m= , n= .13. 平面直角坐标系中一点P(m﹣3,1﹣2m)在第三象限,则m的取值范围是.14. 已知点 的坐标是 ,则点 在第象限.15. 已知点Q(2m2+4,2m2+m+6)在第一象限角平分线上,则m= .16. 下图是利用平面直角坐标系画出的老北京一些地点的示意图,这个坐标系分别以正东和正北方向为x轴和y轴的正方向,如果表示右安门的点的坐标为(-2,-3),表示朝阳门的点的坐标为(3,2),那么表示西便门的点的坐标为 .
 17. 如图,已知直线y= 与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最小值是.
17. 如图,已知直线y= 与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最小值是. 18. 如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°,点M′的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为 .
18. 如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°,点M′的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为 .
三、解答题
-
19. 如果B(m+1,3m﹣5)到x轴的距离与它到y轴的距离相等,求m.20. 在平面直角坐标系,点P(3n+2,4﹣2n)在第四象限,求实数n的取值范围.21. 已知点P(2m+4,m﹣1).试分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,﹣3)点,且与x轴平行的直线上.
22. 已知三角形ABC的两个顶点坐标为A(﹣4,0),B(2,0),如图,且过这两个点的边上的高为4,第三个顶点的横坐标为﹣1,求顶点C的坐标及三角形的面积. 23.
23.如图,是某校的平面示意图,已知图书馆、行政楼的坐标分别为(﹣3,2),(2,3).完成以下问题:
(1)请根据题意在图上建立直角坐标系;
(2)写出图上其他地点的坐标
(3)在图中用点P表示体育馆(﹣1,﹣3)的位置.
 24. 如图,在直角坐标系中,点O1在x轴上,⊙O1与x轴交于点 . 直线y=x+1与坐标轴交于C 、D两点,直线在⊙O1的左侧.
24. 如图,在直角坐标系中,点O1在x轴上,⊙O1与x轴交于点 . 直线y=x+1与坐标轴交于C 、D两点,直线在⊙O1的左侧.
(1)求的面积;
(2)当直线向右平移,第一次与⊙O1相切时,求直线的解析式.25.在平面直角坐标系中,一蚂蚁从原点O出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位,其行走路线如图所示.
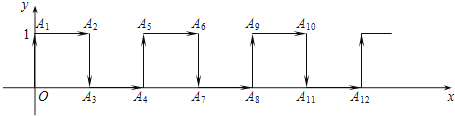
(1)填写下列各点的坐标:A4( , ),A8( , ),A12( , ).
(2)写出点A4n的坐标(n是正整数);
(3)指出蚂蚁从点A100到点A101的移动方向.
26. 在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(x,|x﹣y|),则称点Q为点P的“关联点”.(1)、请直接写出点(2,2)的“关联点”的坐标;(2)、如果点P在函数y=x﹣1的图像上,其“关联点”Q与点P重合,求点P的坐标;(3)、如果点M(m,n)的“关联点”N在函数y=x2的图像上,当0≤m≤2时,求线段MN的最大值.27. 如图,在平面直角坐标系中,给出如下定义:已知点A(2,3),点B(6,3),连接AB.如果线段AB上有一个点与点P的距离不大于1,那么称点P是线段AB的“环绕点”.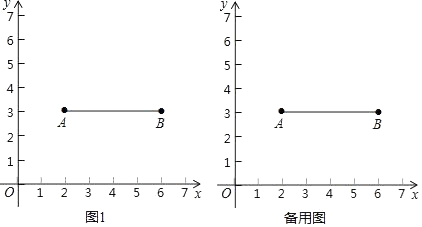 (1)、已知点C(3,1.5),D(4,3.5),E(1,3),则是线段AB的“环绕点”的点是;(2)、已知点P(m,n)在反比例函数y= 的图象上,且点P是线段AB的“环绕点”,求出点P的横坐标m的取值范围;
(1)、已知点C(3,1.5),D(4,3.5),E(1,3),则是线段AB的“环绕点”的点是;(2)、已知点P(m,n)在反比例函数y= 的图象上,且点P是线段AB的“环绕点”,求出点P的横坐标m的取值范围;
(3)、已知⊙M上有一点P是线段AB的“环绕点”,且点M(4,1),求⊙M的半径r的取值范围.28. 在平面直角坐标系中,O为坐标原点,A(m,n+1),B(m+2,n). (1)、当m=1,n=2时.如图1,连接AB、AO、BO.直接写出△ABO的面积为.(2)、如图2,若点A在第二象限、点B在第一象限,连接AB、AO、BO,AB交y轴于H,△ABO的面积为2.求点H的坐标.(3)、若点A、B在第一象限,在y 轴正半轴上存在点C,使得∠CAB=900 , 且CA=AB,求m的值,及OC的长(用含n的式子表示).
(1)、当m=1,n=2时.如图1,连接AB、AO、BO.直接写出△ABO的面积为.(2)、如图2,若点A在第二象限、点B在第一象限,连接AB、AO、BO,AB交y轴于H,△ABO的面积为2.求点H的坐标.(3)、若点A、B在第一象限,在y 轴正半轴上存在点C,使得∠CAB=900 , 且CA=AB,求m的值,及OC的长(用含n的式子表示).