2021-2022学年北师版数学九年级上册期末模拟试题一
试卷更新日期:2021-12-06 类型:期末考试
一、单选题
-
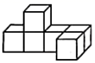
1. 如图所示的几何体是由6个大小相同的小立方块搭成,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 小燕一家三口在商场参加抽奖活动,每人只有一次抽奖机会:在一个 不透明的箱子中装有红、黄、白三种球各 1 个,这些球除颜色外无其他差别,从箱子中随机摸出 1 个球,然后放回箱子中轮到下一个人摸球,三人摸到球的颜色都不相同的概率是( )A、 B、 C、 D、3. 如图,在边长为3的正方形 中, , ,则 的长是( )
2. 小燕一家三口在商场参加抽奖活动,每人只有一次抽奖机会:在一个 不透明的箱子中装有红、黄、白三种球各 1 个,这些球除颜色外无其他差别,从箱子中随机摸出 1 个球,然后放回箱子中轮到下一个人摸球,三人摸到球的颜色都不相同的概率是( )A、 B、 C、 D、3. 如图,在边长为3的正方形 中, , ,则 的长是( )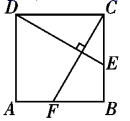 A、1 B、 C、 D、24. 用配方法解方程x2-6x-8=0时,配方结果正确的是( )A、(x-3)2=17 B、(x-3)2=14 C、(x-6)2=44 D、(x-3)2=15. 如图,已知点P是菱形 的对角线 延长线上一点,过点P分别作 、 延长线的垂线,垂足分别为点E、F.若 , ,则 的值为( )
A、1 B、 C、 D、24. 用配方法解方程x2-6x-8=0时,配方结果正确的是( )A、(x-3)2=17 B、(x-3)2=14 C、(x-6)2=44 D、(x-3)2=15. 如图,已知点P是菱形 的对角线 延长线上一点,过点P分别作 、 延长线的垂线,垂足分别为点E、F.若 , ,则 的值为( )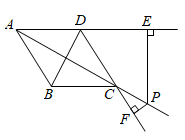 A、 B、 C、2 D、6. 若m、n是一元二次方程x2+3x﹣9=0的两个根,则 的值是( )A、4 B、5 C、6 D、127. 如图,F是线段 上除端点外的一点,将 绕正方形 的顶点A顺时针旋转 ,得到 .连接 交 于点H.下列结论正确的是( )
A、 B、 C、2 D、6. 若m、n是一元二次方程x2+3x﹣9=0的两个根,则 的值是( )A、4 B、5 C、6 D、127. 如图,F是线段 上除端点外的一点,将 绕正方形 的顶点A顺时针旋转 ,得到 .连接 交 于点H.下列结论正确的是( )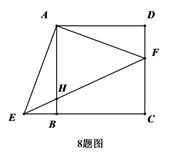 A、 B、 C、 D、8. 在同一时刻,物体的高度与它在阳光下的影长成正比.在某一时刻,有人测得一高为 的竹竿的影长为 ,某一高楼的影长为 ,那么这幢高楼的高度是( )A、 B、 C、 D、9. 如图,在平面直角坐标系中,矩形OABC的OA边在x轴的正半轴上,OC边在y轴的正半轴上,点B的坐标为(4,2),反比例函数 的图象与BC交于点D , 与对角线OB交于点E , 与AB交于点F , 连接OD , DE , EF , DF . 下列结论:① ;② ;③ ;④ .其中正确的结论有( )
A、 B、 C、 D、8. 在同一时刻,物体的高度与它在阳光下的影长成正比.在某一时刻,有人测得一高为 的竹竿的影长为 ,某一高楼的影长为 ,那么这幢高楼的高度是( )A、 B、 C、 D、9. 如图,在平面直角坐标系中,矩形OABC的OA边在x轴的正半轴上,OC边在y轴的正半轴上,点B的坐标为(4,2),反比例函数 的图象与BC交于点D , 与对角线OB交于点E , 与AB交于点F , 连接OD , DE , EF , DF . 下列结论:① ;② ;③ ;④ .其中正确的结论有( ) A、4个 B、3个 C、2个 D、1个10. 如图,函数 与 的图象相交于点 两点,则不等式 的解集为( )
A、4个 B、3个 C、2个 D、1个10. 如图,函数 与 的图象相交于点 两点,则不等式 的解集为( )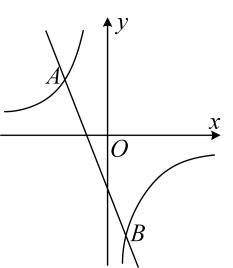 A、 B、 或 C、 D、 或11. 如图,点A在反比例函数 图象上, 轴于点B , C是OB 的中点,连接 AO , AC ,若 的面积为2,则k= ( )
A、 B、 或 C、 D、 或11. 如图,点A在反比例函数 图象上, 轴于点B , C是OB 的中点,连接 AO , AC ,若 的面积为2,则k= ( ) A、4 B、8 C、12 D、1612. 在锐角 中,分别以AB和AC为斜边向 的外侧作等腰 和等腰 ,点D、E、F分别为边AB、AC、BC的中点,连接MD、MF、FE、FN . 根据题意小明同学画出草图(如图所示),并得出下列结论:① ,② ,③ ,④ ,其中结论正确的个数为( )
A、4 B、8 C、12 D、1612. 在锐角 中,分别以AB和AC为斜边向 的外侧作等腰 和等腰 ,点D、E、F分别为边AB、AC、BC的中点,连接MD、MF、FE、FN . 根据题意小明同学画出草图(如图所示),并得出下列结论:① ,② ,③ ,④ ,其中结论正确的个数为( )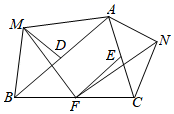 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
13. 如图,矩形 , , ,点 在 轴正半轴上,点 在 轴正半轴上.当点 在 轴上运动时,点 也随之在 轴上运动,在这个运动过程中,点 到原点 的最大距离为 .
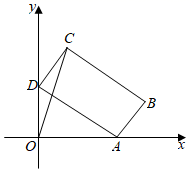 14. 如图,矩形 中, , ,对角线 的垂直平分线 交 于点 、交 于点 ,则线段 的长为.
14. 如图,矩形 中, , ,对角线 的垂直平分线 交 于点 、交 于点 ,则线段 的长为.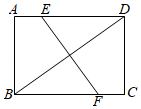 15. 如图,点A是反比例函数 的图象上一点,过点A作 轴于点C, 交反比例函数 的图象于点B,点P是y轴正半轴上一点.若 的面积为2,则k的值为.
15. 如图,点A是反比例函数 的图象上一点,过点A作 轴于点C, 交反比例函数 的图象于点B,点P是y轴正半轴上一点.若 的面积为2,则k的值为.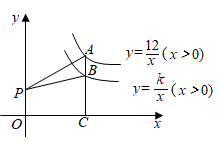 16. 如图,将一把矩形直尺 和一块等腰直角三角板 摆放在平面直角坐标系中, 在 轴上,点 与点 重合,点 在 上, 交 于点 ,反比例函数 的图象恰好经过点 , ,若直尺的宽 ,三角板的斜边 ,则 .
16. 如图,将一把矩形直尺 和一块等腰直角三角板 摆放在平面直角坐标系中, 在 轴上,点 与点 重合,点 在 上, 交 于点 ,反比例函数 的图象恰好经过点 , ,若直尺的宽 ,三角板的斜边 ,则 .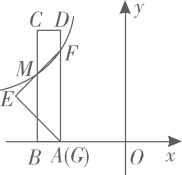 17. 如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是 .
17. 如图,正方形OABC的边长为2,将正方形OABC绕点O逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是 .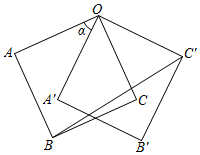 18. 如图,在正方形 中,点O是对角线 的中点,点P在线段 上,连接 并延长交 于点E,过点P作 交 于点F,连接 、 , 交 于G,现有以下结论:① ;② ;③ ;④ 为定值;⑤ .以上结论正确的有(填入正确的序号即可).
18. 如图,在正方形 中,点O是对角线 的中点,点P在线段 上,连接 并延长交 于点E,过点P作 交 于点F,连接 、 , 交 于G,现有以下结论:① ;② ;③ ;④ 为定值;⑤ .以上结论正确的有(填入正确的序号即可).
三、解答题
-
19. 列方程(组)解应用题
端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?
20. 如图, 、 、 分别是 各边的中点,连接 、 、 .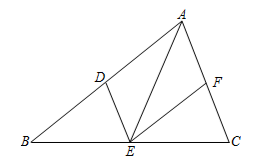 (1)、求证:四边形 为平行四边形;(2)、加上条件 ▲ 后,能使得四边形 为菱形,请从① ;② 平分 ;③ ,这三个条件中选择条件填空(写序号),并加以证明.21. 为庆祝中国共产党建党100周年,某校开展了“党在我心中”党史知识竞赛,竞赛得分为整数,王老师为了解竞赛情况,随机抽取了部分参赛学生的得分并进行整理,绘制成如下不完整的统计图表:
(1)、求证:四边形 为平行四边形;(2)、加上条件 ▲ 后,能使得四边形 为菱形,请从① ;② 平分 ;③ ,这三个条件中选择条件填空(写序号),并加以证明.21. 为庆祝中国共产党建党100周年,某校开展了“党在我心中”党史知识竞赛,竞赛得分为整数,王老师为了解竞赛情况,随机抽取了部分参赛学生的得分并进行整理,绘制成如下不完整的统计图表:
组别
成绩 (分)
频数
A
75.5
6
B
14
C
D
E
请你根据上面的统计图表提供的信息解答下列问题:
(1)、上表中的 , , .(2)、这次抽样调查的成绩的中位数落在哪个组?请补全频数分布直方图.(3)、已知该校有1000名学生参赛,请估计竞赛成绩在90分以上(不含90分)的学生有多少人?(4)、现要从E组随机抽取两名学生参加上级部门组织的党史知识竞赛,E组中的小丽和小洁是一对好朋友,请用列表或画树状图的方法求出恰好抽到小丽和小洁的概率.22. 如图,一次函数 的图象与反比例函数 的图象相交于 、 两点.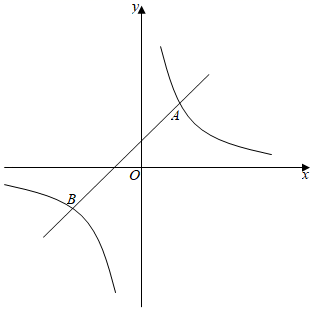 (1)、求一次函数和反比例函数的解析式;(2)、根据图象,直接写出满足 的 的取值范围;(3)、若点 在线段 上,且 ,求点 的坐标.23. 如图,在平行四边形 中,E为 边的中点,连接 ,若 的延长线和 的延长线相交于点F.
(1)、求一次函数和反比例函数的解析式;(2)、根据图象,直接写出满足 的 的取值范围;(3)、若点 在线段 上,且 ,求点 的坐标.23. 如图,在平行四边形 中,E为 边的中点,连接 ,若 的延长线和 的延长线相交于点F.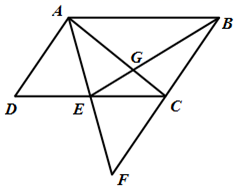 (1)、求证: ;(2)、连接 和 相交于点为G,若 的面积为2,求平行四边形 的面积.24. 阅读理解:
(1)、求证: ;(2)、连接 和 相交于点为G,若 的面积为2,求平行四边形 的面积.24. 阅读理解:材料一:若三个非零实数x , y , z满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实教x , y , z构成“和谐三数组”.
材料二:若关于x的一元二次方程ax2+bx +c= 0(a≠0)的两根分别为 , ,则有 , .
问题解决:
(1)、请你写出三个能构成“和谐三数组”的实数;(2)、若 , 是关于x的方程ax2+bx +c= 0 (a , b , c均不为0)的两根, 是关于x的方程bx+c=0(b , c均不为0)的解.求证:x1 ,x2 , x3可以构成“和谐三数组”;(3)、若A(m , y1) ,B(m + 1,y2) ,C(m+3,y3)三个点均在反比例函数 的图象上,且三点的纵坐标恰好构成“和谐三数组”,求实数m的值.25. 已知正方形 , , 为平面内两点. (1)、(探究建模)
(1)、(探究建模)
如图1,当点 在边 上时, ,且 , , 三点共线.求证: ;(2)、(类比应用)
如图2,当点 在正方形 外部时, , ,且 , , 三点共线.猜想并证明线段 , , 之间的数量关系;(3)、(拓展迁移)
如图3,当点 在正方形 外部时, , , ,且 , , 三点共线, 与 交于 点.若 , ,求 的长.