天津市河西区2021-2022学年八年级上学期期中数学试题
试卷更新日期：2021-12-06 类型：期中考试
一、单选题
-
1. 在平面直角坐标系中，点（5，2）关于x轴对称的点的坐标为（ ）A、（5，－2） B、（－5，2） C、（2，5） D、（2，－5）2. 以下冬奥会图标中，是轴对称图形的是（ ）A、
B、
C、
D、
3. 下面图形中具有稳定性的是（ ）A、
B、
C、
D、
4. 下面四个图形中，线段BE能表示三角形ABC的高的是（ ）A、
B、
C、
D、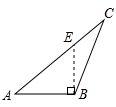
5. 下列每组数分别是三根木棒的长度，能用它们首尾相连摆成一个三角形的是（ ）A、3cm，4cm，8cm B、8cm，7cm，15cm C、5cm，5cm，11cm D、13cm，12cm，20cm6. 下列说法错误的是（ ）A、三边分别相等的两个三角形全等 B、三角分别相等的两个三角形全等 C、两边和它们的夹角分别相等的两个三角形全等 D、斜边和一条直角边分别相等的两个直角三角形全等7. 工人常用角尺平分一个任意角，做法如下：如图， 是一个任意角，在边 、 上分别取 ，移动角尺，使角尺两边相同的刻度分別与点 、 重合，过角尺顶点 作射线 ，由此作法便可得 ，共依据是（ ）
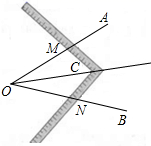A、 B、 C、 D、8. △ABC的两条角平分线AD ， BE相交于点F ， 下列结论一定正确的是（ ）
A、BD = DC B、BE⊥AC C、FA = FB D、点F到三角形三边的距离都相等9. 若一个多边形的每一个内角均为120°，则下列说法错误的是（ ）A、这个多边形的内角和为720° B、这个多边形的边数为6 C、这个多边形是正多边形 D、这个多边形的外角和为360°10. 如图所示，三角形纸片ABC中，∠A＝65°，∠B＝75°，将纸片的一角折叠，使点C落在△ABC内，若∠1＝20°，则∠2的度数为（ ）
A、25° B、30° C、40° D、60°二、填空题
-
11. 下图中的x的值为 ．
12. 图中与标号“1”的三角形成轴对称的三角形的个数为 ．
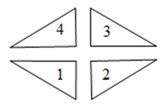
13. 如图，以正方形ABCD的中心O为原点建立平面直角坐标系，若点A的坐标为（－2，－2），则点 的坐标是 ．
14. 如图，已知∠C＝∠D ， ∠ABC＝∠BAD ， AC与BD相交于点E ， 请你写出图中一组相等的线段 ． （写出一组即可）
15. 如图， ， ， ， ，垂足分别是点 、 ， ， ，则 的长是.
16. 如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC＝9，CD＝4，则四边形ABCD的面积是.
三、解答题
-
17. 在下图给出一个图案的左半部分，其中虚线是这个图案的对称轴．请你画出这个图案的右半部分，使它组成一个完整的图案．
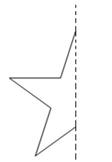
18. 用一条长为 的细绳围成一个等腰三角形.(1)、如果腰长是底边长的2倍，那么各边的长是多少？(2)、能围成有一边长是 的等腰三角形吗？为什么？19. 如图，电信部门要在S区修建一座电视信号发射塔，按照设计要求，发射塔到两个城镇A，B的距离必须相等，到两条高速公路m和n的距离也必须相等，发射塔应修建在什么位置？在图上标出它的位置．（要求用尺规作图，保留作图痕迹，不写作法，要写明结论）
20. 在平面直角坐标系中，点A（3，0），点B（0，5）和点C（0，3）．
(1)、请直接写出OB的长度：OB=；(2)、如图：若点D在x轴上，且点D的坐标为（－5，0），求证：△AOB≌△COD ．21. 如图，在△ABC 中，∠ABC=60°，∠ACB=82°，延长CB至D ， 使DB=BA ， 延长BC至E ， 使CE=CA ， 连接AD ， AE ． 求∠D ， ∠E ， ∠DAE 的度数．
