山西省晋中市寿阳县2021-2022学年八年级期中数学试题

试卷更新日期：2021-12-06 类型：期中考试

进入出卷网下载

一、单选题

1. 若点 $P$ 的坐标是（2，﹣1），则点 $P$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 在实数 $\frac{22}{7} ， 3.14159265 ， \sqrt[3]{9} ， - 8 ， \sqrt[3]{2} ， \sqrt{36} ， \frac{π}{3}$ 中，无理数的个数为（　　）

A、1 B、2 C、3 D、4

查看试题解析
3. 下列二次根式中，属于最简二次根式的是（　　）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{0.8}$ C、 $\sqrt{9}$ D、 $\sqrt{5}$

查看试题解析
4. 在勾股定理的学习过程中，我们已经学会了运用以下图形，验证著名的勾股定理：这种根据图形直观推论或验证数学规律和公式的方法，简称为“无字证明”．实际上它也可用于验证数与代数，图形与几何等领域中的许多数学公式和规律，它体现的数学思想是（）

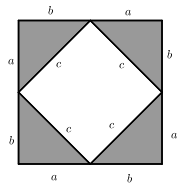
A、统计思想 B、分类思想 C、数形结合思想 D、函数思想

查看试题解析
5. 下列计算正确的是（　　）

A、 $3 + \sqrt{3} = 3 \sqrt{3}$ B、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ C、 $\sqrt{12} = \pm 2 \sqrt{3}$ D、 $\sqrt{3} + \sqrt{12} = 3 \sqrt{3}$

查看试题解析
6. 下列条件中，不能判断一个三角形是直角三角形的是（　　）

A、三条边的长度比为1：2：3 B、三个角的度数比为1：2：3 C、三条边满足关系 $a^{2} + b^{2} = c^{2}$ D、三个角满足关系∠B+∠C=∠A

查看试题解析
7. 如图，在平面直角坐标系中，点 $A (3 ， m)$ 在第一象限，若点 $A$ 关于 $x$ 轴的对称点 $B$ 在直线 $y = - x + 1$ 上，则 $m$ 的值为（）

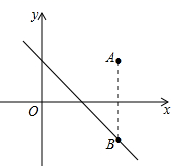A、-1 B、1 C、2 D、3

查看试题解析
8. 一次函数y＝（k+3）x+b（k＞0，b＜0）在平面直角坐标系中的图象大致是（　　）

A、 B、 C、 D、

查看试题解析
9. 把 $y = 2 x + 1$ 的图像沿y轴向下平移5个单位后所得图象的关系式是（）

A、 $y = 2 x + 5$ B、 $y = 2 x + 6$ C、 $y = 2 x - 4$ D、 $y = 2 x + 4$

查看试题解析
10. 如图所示，小明准备测量一段河水的深度，他把一根竹竿竖直插到离岸边1.5m远的水底，竹竿高出水面0.5m，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为（）

A、2m B、2.25m C、2.5m D、3m

查看试题解析

二、填空题

11. 已知 $a - 1$ 的平方根是 $\pm 2$ ，则 $a$ 的值为.

查看试题解析
12. 若点 $(- 4, y_{1}), (2, y_{2})$ 都在直线 $y = - x + b$ 上，则 $y_{1}$ $y_{2}$ .（填“ $>$ ”“ $<$ ”或“ $=$ ” ）

查看试题解析
13. 如图， $R t Δ A B C$ 中， $A B = 18 ， B C = 12 ， ∠ B = 90 °$ ，将 $Δ A B C$ 折叠，使点 $A$ 与 $B C$ 的中点 $D$ 重合，折痕为 $M N ，$ 则线段 $B N$ 的长为．

查看试题解析
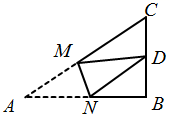14. 某地出租车计费方法如图所示，其中x（单位：km）表示行驶里程，y（单位：元）表示车费．若某乘客一次乘出租车的里程为5km，则这位乘客需支付的费用为元．

查看试题解析
15. 如图，用两个面积为3cm²的小正方形纸片剪拼成一个大的正方形，则以数轴上表示1的点A为圆心，以大正方形的边长为半径画弧，与数轴的交点表示的实数是．

查看试题解析

三、解答题

16. 计算

(1)、 $\sqrt{5} \times \sqrt{\frac{9}{20}}$

(2)、 $(\sqrt{\frac{9}{2}} - \frac{\sqrt{50}}{3}) \times \sqrt{2}$

(3)、 $\sqrt{4} - \frac{\sqrt{8} - \sqrt{18}}{\sqrt{2}}$

(4)、 ${(\sqrt{3} - 1)}^{2} - (1 + \sqrt{3}) (2 - \sqrt{3})$

查看试题解析
17. 如图的正方形网格中，有一个不完整的平面直角坐标系，其中 $△ A B C$ 的顶点 $A$ ， $B$ 的坐标分别是 $(- 2 ， 3)$ ， $(- 4 ， 2)$ ，点 $C$ 恰好在格点上．

(1)、请在图中画出 $x$ 轴，并标明原点 $O$ 的位置；

(2)、图中点 $C$ 的坐标为；

(3)、将 $A$ ， $B$ ， $C$ 三点的横坐标分别乘-1，纵坐标不变，得到 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 三点，请在该坐标系中画出 $△ A^{'} B^{'} C^{'}$ ，并直接写出 $△ A^{'} B^{'} C^{'}$ 与 $△ A B C$ 的位置关系．

查看试题解析
18. 已知，一次函数 $y = - \frac{1}{2} x + 3$ 的图象与 $x$ 轴交于点A ，与y轴交于点B ．

(1)、求A、B两点的坐标；

(2)、画出该函数图象；

(3)、求AB的长．

查看试题解析
19. 交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度，所用的经验公式是 $v = 16 \sqrt{d f}$ ，其中 $v$ 表示车速（单位：km/h）， $d$ 表示刹车后车轮滑过的距离（单位：m）， $f$ 表示摩擦因数．在某次交通事故调查中，测得 $d = 20$ m， $f = 1.2$ ，该路段限速60km/h，该汽车超速了吗？请说明理由（已知： $\sqrt{2} \approx 1.4 ， \sqrt{3} \approx 1.7$ ）

查看试题解析
20. 如图，在△ACD中，AD＝17，AC＝15，DC＝8，点B是CD延长线上一点，连接AB，若AB＝25．求：△ABD的面积．

查看试题解析
21. 《九章算术》中记载，浮箭漏（图①）出现于汉武帝时期，它由供水壶和箭壶组成，箭壶内装有箭尺，水匀速地从供水查流到箭壶，箭壶中的水位逐渐上升，箭尺匀速上浮，可通过读取箭尺读数计算时间，某学校STEAM小组仿制了一套浮箭漏，并从函数角度进行了如下实验探究：
（实验观察）实验小组通过观察，每2小时记录次箭尺读数，得到下表：

供水时间x（小时）

0

2

4

6

8

箭尺读数y（厘米）

6

18

30

42

54

（探索发现）

(1)、建立平面直角坐标系，如图②，横轴表示供水时间x ．纵轴表示箭尺读数y ，描出以表格中数据为坐标的各点．

(2)、观察上述各点的分布规律，判断它们是否在同一条直线上，如果在同一条直线上，求出这条直线所对应的函数表达式，如果不在同一条直线上，说明理由．
（结论应用）应用上述发现的规律估算：

(3)、供水时间达到12小时时，箭尺的读数为多少厘米？

(4)、如果本次实验记录的开始时间是上午8：00，那么当箭尺读数为90厘米时是几点钟？（箭尺最大读数为100厘米）

查看试题解析
22. 阅读下列材料并完成任务：“最短路径问题”是数学中一类具有挑战性的问题．其实，数学史上也有不少相关的故事，如下即为其中较为经典的一则：古希腊有一位久负盛名的学者，名叫海伦．他精通数学，物理，聪慧过人．有一天，一位将军向他请教一个问题：如图1，将军从甲地骑马出发，要到河边让马饮水，然后再回到乙地的马棚，为使马走的路程最短，应该让马在什么地方饮水？海伦认为以河边为镜面，画出甲地的镜像点(垂直河边的等距离点)，然后连接乙地和甲地的镜像点，会跟河边相交一点，这个点就是马饮水的地方，马走的路程最短(两点之间直线距离最短)．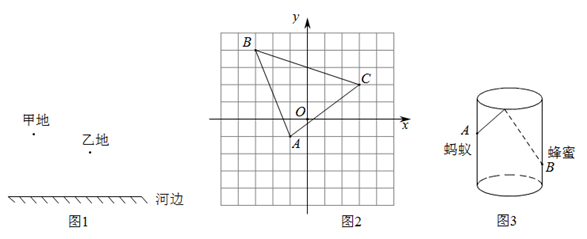

任务：

(1)、请你帮海伦在图1的位置完成作图，并标出马饮水的地点P（画出草图即可）；

(2)、如图2， $△$ ABC的三个顶点的坐标分别为A(-1，-1)，B(-3，4)，C(3，2)．请你在x轴上找一点Q ，使得QB+QC最小（保留作图痕迹）；

(3)、应用：
如图3，圆柱形容器高为18cm，底面周长为24cm．在杯内壁离杯底4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm处的点A处，点A与B的水平距离等干底面直径，求蚂蚁从外壁A处到达内壁B处的最短距离．

查看试题解析
23. 已知在平面直角坐标系中，直线 $y_{1} = k_{1} x + 4 (k_{1} \neq 0)$ 与直线 $y_{2} = k_{2} x (k_{2} \neq 0)$ 交于点 $C (6 ， 12)$ ，直线 $y_{1}$ 分别与 $x$ 轴， $y$ 轴交于点 $A$ 和点 $B$ ．

(1)、求直线 $y_{1}$ 与 $y_{2}$ 的表达式及点 $A$ ，点 $B$ 的坐标；

(2)、 $x$ 轴上是否存在点 $P$ ，使 $Δ A C P$ 的面积为 $30$ ，若存在，求出点 $P$ 的坐标；若不存在，说明理由；

(3)、 $x$ 轴上是否存在点 $Q$ ，使 $Δ O C Q$ 为等腰三角形，若存在，请直接写出点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析

供水时间x（小时）	0	2	4	6	8
箭尺读数y（厘米）	6	18	30	42	54