山东省枣庄市薛城区2021-2022学年八年级上学期期中数学试题
试卷更新日期:2021-12-06 类型:期中考试
一、单选题
-
1. 下列各组数中,是勾股数的是( )A、1,1, B、1.5,2.5,2 C、4,5,6 D、9,12,152. 在平面直角坐标系中,点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 勾股定理是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中不能证明勾股定理的是( )A、
 B、
B、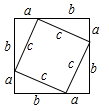 C、
C、 D、
D、 4. 将一次函数y=﹣3x的图象沿y轴向下平移4个单位长度后,所得图象的函数表达式为( )A、y=﹣3(x﹣4) B、y=﹣3x+4 C、y=﹣3(x+4) D、y=﹣3x﹣45. 下列计算中,正确的是( )A、 B、 C、 D、6. 如图, 中, , , , 是 边上的中线,则 的长度为( )
4. 将一次函数y=﹣3x的图象沿y轴向下平移4个单位长度后,所得图象的函数表达式为( )A、y=﹣3(x﹣4) B、y=﹣3x+4 C、y=﹣3(x+4) D、y=﹣3x﹣45. 下列计算中,正确的是( )A、 B、 C、 D、6. 如图, 中, , , , 是 边上的中线,则 的长度为( )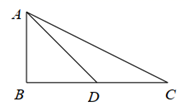 A、1 B、2 C、 D、7. 若点A(a , 3)与B(2,b)关于x轴对称,则点M(a , b)的坐标为( )A、(﹣2,3) B、(2,3) C、(2,﹣3) D、(﹣2,﹣3)8. 如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB 剪开,所得的圆柱侧面展开图是( )
A、1 B、2 C、 D、7. 若点A(a , 3)与B(2,b)关于x轴对称,则点M(a , b)的坐标为( )A、(﹣2,3) B、(2,3) C、(2,﹣3) D、(﹣2,﹣3)8. 如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB 剪开,所得的圆柱侧面展开图是( )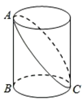 A、
A、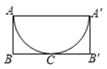 B、
B、 C、
C、 D、
D、 9. 如图,数轴上的点 分别对应的数是 ,那么表示 的点应在( )
9. 如图,数轴上的点 分别对应的数是 ,那么表示 的点应在( ) A、线段 上 B、线段 上 C、线段 上 D、线段 上10. 习近平总书记在全国教育大会上强调,要坚持中国特色社会主义教育发展道路.培养德智体美劳全面发展的社会主义建设者和接班人.枣庄某学校利用周未开展课外劳动实践活动.如图反映的过程是:小强从家去菜地浇水,又去玉米地除草,然后回家.如果菜地和玉米地的距离为a千米,小强在玉米地除草比在菜地浇水多用的时间为b分钟,则a , b的值分别为( )
A、线段 上 B、线段 上 C、线段 上 D、线段 上10. 习近平总书记在全国教育大会上强调,要坚持中国特色社会主义教育发展道路.培养德智体美劳全面发展的社会主义建设者和接班人.枣庄某学校利用周未开展课外劳动实践活动.如图反映的过程是:小强从家去菜地浇水,又去玉米地除草,然后回家.如果菜地和玉米地的距离为a千米,小强在玉米地除草比在菜地浇水多用的时间为b分钟,则a , b的值分别为( ) A、1.1,8 B、0.9,3 C、1.1,12 D、0.9,811. 已知x为实数,且 ﹣ =0,则x2+x﹣3的算术平方根为( )A、3 B、2 C、3和﹣3 D、2和﹣212. 如图,在 的正方形网格中,每个小正方形的边长均为1,点 , , 都在格点上,若 是 的边 上的高,则 的长为( )
A、1.1,8 B、0.9,3 C、1.1,12 D、0.9,811. 已知x为实数,且 ﹣ =0,则x2+x﹣3的算术平方根为( )A、3 B、2 C、3和﹣3 D、2和﹣212. 如图,在 的正方形网格中,每个小正方形的边长均为1,点 , , 都在格点上,若 是 的边 上的高,则 的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 64的平方根是 .14. 如图,某吉祥物所处的位置分别为M(﹣2,2)、B(1,1),则A、C、N三点中为坐标原点的是点.
 15. 如图,在△ABC中,∠ABC=90°,AC=10,AB=8,若两阴影部分都是正方形,C、D、E在一条直线上,且它们的面积之比为1:3,则较大的正方形的面积 .
15. 如图,在△ABC中,∠ABC=90°,AC=10,AB=8,若两阴影部分都是正方形,C、D、E在一条直线上,且它们的面积之比为1:3,则较大的正方形的面积 . 16. 如图,小冰想用一条彩带缠绕圆柱4圈,正好从A点绕到正上方的B点,已知圆柱底面周长是3m,高为5m,则所需彩带最短是m.
16. 如图,小冰想用一条彩带缠绕圆柱4圈,正好从A点绕到正上方的B点,已知圆柱底面周长是3m,高为5m,则所需彩带最短是m. 17. 在平面直角坐标系中,点O为坐标原点,若直线y=﹣5x+5与x轴、y轴分别交于点A , B , 则△AOB的面积为 .18. 如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点“P到x轴的距离为2,则P点的坐标为.
17. 在平面直角坐标系中,点O为坐标原点,若直线y=﹣5x+5与x轴、y轴分别交于点A , B , 则△AOB的面积为 .18. 如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点“P到x轴的距离为2,则P点的坐标为.三、解答题
-
19. 请在数轴上用尺规作出 所对应的点.(保留作图痕迹,不写做法)20. 计算:(1)、 ﹣4;(2)、(2﹣ )2×(6+4 ).21. 如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E , 将△ADE折叠使点D恰好落在BC边上的点F , 求CE的长.
 22. 如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
22. 如图,在直角坐标平面内,已知点A的坐标(﹣2,0). (1)、根据图形画出B关于原点对称的点C , 点A关于y轴对称的点D , 并写出点 的坐标;(2)、点B关于原点对称的点C的坐标是;点A关于y轴对称的点D的坐标是;(3)、四边形ABDC的面积是;(4)、在y轴上找一点F , 使S△ADF= S△ABD , 那么点F的坐标是 .23. 如图,E、F是等腰Rt△ABC的斜边BC上的两动点,∠EAF=45°,CD⊥BC且CD=BE .
(1)、根据图形画出B关于原点对称的点C , 点A关于y轴对称的点D , 并写出点 的坐标;(2)、点B关于原点对称的点C的坐标是;点A关于y轴对称的点D的坐标是;(3)、四边形ABDC的面积是;(4)、在y轴上找一点F , 使S△ADF= S△ABD , 那么点F的坐标是 .23. 如图,E、F是等腰Rt△ABC的斜边BC上的两动点,∠EAF=45°,CD⊥BC且CD=BE . (1)、求证:△ABE≌△ACD;(2)、求证:EF2=BE2+CF2 .24. 如图,一次函数 的图象与 和 分别交于点 和点 ,与正比例函数 图象交于点 .
(1)、求证:△ABE≌△ACD;(2)、求证:EF2=BE2+CF2 .24. 如图,一次函数 的图象与 和 分别交于点 和点 ,与正比例函数 图象交于点 . (1)、求m和n的值(2)、求 的面积(3)、在直线 上是否存在异与点 的另一点 ,使得 与 的面积相等?若存在,请求出 点的坐标;若不存在,请说明理由.25. 我国边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防部迅速派出快艇B追赶(如图1).图2中l1、l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.根据图象回答问题:
(1)、求m和n的值(2)、求 的面积(3)、在直线 上是否存在异与点 的另一点 ,使得 与 的面积相等?若存在,请求出 点的坐标;若不存在,请说明理由.25. 我国边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防部迅速派出快艇B追赶(如图1).图2中l1、l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系.根据图象回答问题: (1)、直线l1与直线l2中表示B到海岸的距离与追赶时间之间的关系(2)、A与B比较,速度快;(3)、l1与l2对应的两个一次函数表达式S1=k1t+b1与S2=k2t+b2中,k1、k2的实际意义各是什么?并直接写出两个具体表达式(4)、15分钟内B能否追上A?为什么?(5)、当A逃离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?为什么?
(1)、直线l1与直线l2中表示B到海岸的距离与追赶时间之间的关系(2)、A与B比较,速度快;(3)、l1与l2对应的两个一次函数表达式S1=k1t+b1与S2=k2t+b2中,k1、k2的实际意义各是什么?并直接写出两个具体表达式(4)、15分钟内B能否追上A?为什么?(5)、当A逃离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?为什么?