山东省青岛市即墨区2021-2022学年八年级上学期期中数学试题

试卷更新日期：2021-12-06 类型：期中考试

进入出卷网下载

一、单选题

1. 下列实数﹣ $\frac{π}{2}$ ， $\frac{1}{3}$ ，|﹣3|， $\sqrt{4}$ ， $\sqrt[3]{- 8}$ ， $\sqrt{7}$ ，0.4040404…（每相邻两个4之间一个0）中，无理数有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 若点A（﹣3，a）与B（b ， 2）关于x轴对称，则点M（a ， b）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 与 $\sqrt{17}$ ＋1最接近的整数是（）

A、4 B、5 C、6 D、8

查看试题解析

4. 变量x ， y的一些对应值如表：

x	…	﹣2	﹣1	0	1	2	3	…
y	…	4	2	0	﹣2	﹣4	﹣6	…

根据表格中的数据规律，当x＝11时，y的值是（）

A、﹣22 B、﹣11 C、11 D、22

查看试题解析

5. 如图，在 $3 \times 3$ 的正方形网格中，每个小正方形的边长均为1，点 $A$ ， $B$ ， $C$ 都在格点上，若 $B D$ 是 $△ A B C$ 的边 $A C$ 上的高，则 $B D$ 的长为（）

A、 $\frac{5}{13} \sqrt{26}$ B、 $\frac{10}{13} \sqrt{26}$ C、 $\frac{13}{7} \sqrt{13}$ D、 $\frac{7}{13} \sqrt{13}$

查看试题解析
6. 已知一次函数 $y_{1} = a x + b$ 和 $y_{2} = b x + a$ $(a \neq b)$ ，函数 $y_{1}$ 和 $y_{2}$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
7. 小华和小明是同班同学，也是邻居，某日早晨，小明7：40先出发去学校，走了一段后，在途中停下吃了早餐，后来发现上学时间快到了，就跑步到学校；小华离家后直接乘公共汽车到了学校，如图是他们从家到学校已走的路程 $S$ （米）和所用时间 $t$ （分钟）的关系图，则下列说法中错误的是（）

A、小明家和学校距离1200米 B、小华乘公共汽车的速度是240米/分 C、小华乘坐公共汽车后7：50与小明相遇 D、小明从家到学校的平均速度为80米/分

查看试题解析
8. 如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD ，正方形EFGH ，正方形MNPQ的面积分别为S₁ ， S₂ ， S₃ ，若S₁＋S₂＋S₃＝60，则S₂的值是（）

A、12 B、15 C、20 D、25

查看试题解析

二、填空题

9. 若x³＝64，则 $\sqrt{x}$ ＝．

查看试题解析
10. 如果一个正数的两个平方根是2a＋1和4﹣3a ，那么这个正数是．

查看试题解析
11. 如图是一机器人比赛行走的路径，机器人从A处先往东走8m ，又往北走3m ，遇到障碍后又往西走4m ，再转向北走9m往东拐，仅走1m就到达了B ．问A、B两点之间的距离为m ．

查看试题解析
12. 已知一次函数y＝kx＋b的图象不经过第三象限，且点（1，y₁），（﹣1，y₂）在该函数图象上，则y₁ ， y₂的大小关系是y₁y₂（用“＞、＜、＝”连接）

查看试题解析
13. 如图，过点A（0，3）的一次函数的图象与正比例函数y＝2x的图象相交于点B ，这个一次函数的表达式是．

查看试题解析
14. 小明和小颖下棋，小明执圆子，小颖执方子．如图，棋盘中心方子的位置用（0，﹣1）表示，右上角方子的位置用（1，0）表示．小明将第4枚圆子放入棋盘后，所有棋子构成一个轴对称图形．他放的位置可以表示为．

查看试题解析
15. 如图，已知圆柱底面的周长为8dm ，圆柱高为4dm ，在圆柱的侧面上，过点A和点C嵌有一圈金属丝，则这圈金属丝的周长最小为dm ．

查看试题解析
16. 如图，一个粒子在第一象限内及x轴、y轴上运动，在第一分钟，它从原点运动到点（1，0），第二分钟，它从点（1，0）运动到点（1，1），而后它接着按图中箭头所示在与x轴，y轴平行的方向上来回运动，且每分钟移动1个单位长度，那么在第2022分钟时，这个粒子所在位置的坐标是．

查看试题解析

三、解答题

17. 在数轴上作出﹣ $\sqrt{10}$ 的对应点.

查看试题解析
18. 计算题

(1)、 $- \sqrt[3]{27}$ ＋2 $\sqrt{12}$ ＋3 $\sqrt{48}$ ；

(2)、（ $\sqrt{12} - \sqrt{\frac{2}{3}}$ ）× $\sqrt{3}$ ；

(3)、 $\frac{2 \sqrt{12} + \sqrt{3}}{\sqrt{3}} +$ （1﹣ $\sqrt{3}$ ）⁰；

(4)、（ $\sqrt{5}$ ＋1）（ $\sqrt{5}$ ﹣1）﹣ $\sqrt{27}$ ．

查看试题解析
19. 如图，在正方形网格中，每个小正方形的边长都为1，点A ，点B在网格中的位置如图所示．

(1)、①请在下面方格纸中建立适当的平面直角坐标系，使点A、点B的坐标分别为（1，﹣3）、（4，﹣2）；
②点C的坐标为（2，﹣1），在平面直角坐标系中标出点C的位置，连接AB ， BC ， CA ，则ABC的面积为　 ▲　

(2)、在图中画出△ABC关于y轴对称的图形△A₁B₁C₁ ，并写出各点坐标：A₁（），B₁（），C₁（）；

(3)、在x轴上找到一点P ，使△ABP的周长最小，直接写出这个周长的最小值：．

查看试题解析
20. 笔直的河流一侧有一营地C ，河边有两个漂流点A ， B、其中AB＝AC ，由于周边施工，由C到A的路现在已经不通，为方便游客，在河边新建一个漂流点H（A ， H ， B在同一直线上），并新修一条路CH ，测得BC＝10千米，CH＝8千米，BH＝6千米．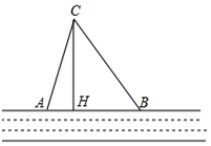

(1)、判断△BCH的形状，并说明理由；

(2)、求原路线AC的长．

查看试题解析
21. 某剧院举行新年专场音乐会，成人票每张40元，学生票每张10元，剧院制定了两种优惠方案，且每个团体购票时只能选择其中一种优惠方案，方案1：购买一张成人票赠送一张学生票；方案2：按总价的90%付款．某校有4名老师与x（x≥4）名学生去观赏这次音乐会，设用方案1和方案2付款的总金额分别为y₁（元）和y₂（元）．

(1)、分别求出y₁、y₂与x之间的函数关系式；

(2)、当学生人数为20名时，请通过计算说明哪种方案更优惠；

(3)、请通过计算说明：当学生人数为多少时，选择两种方案一样优惠？

查看试题解析
22. 如图，直线l₁：y₁＝ax﹣a ， l₁与x轴交于点B ，直线l₂：y₂＝ $\frac{3}{2}$ x＋b ， l₂与x轴交于点A ，直线l₁ ， l₂交于点C（2，﹣3）．

(1)、a＝；点B的坐标为；

(2)、求直线l₂的解析表达式；

(3)、求△ABC的面积．

查看试题解析
23. （背景介绍）勾股定理是几何学中的明珠，充满着魅力．千百年来，人们对它的证明趋之若鹜，其中有著名的数学家，也有业余数学爱好者．向常春在1994年构造发现了一个新的证法．

（小试牛刀）把两个全等的直角三角形△ABC和△DAE如图1放置，其三边长分别为a ， b ， c ．显然，∠DAB＝∠B＝90°，AC⊥DE ．请用a ， b ， c分别表示出梯形ABCD ，四边形AECD ， △EBC的面积：

S_梯形ABCD＝，

S_△EBC＝，

S_{四边形AECD}＝，

再探究这三个图形面积之间的关系，它们满足的关系式为，化简后，可得到勾股定理．

（知识运用）

如图2，河道上A ， B两点（看作直线上的两点）相距200米，C ， D为两个菜园（看作两个点），AD⊥AB ， BC⊥AB ，垂足分别为A ， B ， AD＝80米，BC＝70米，现在菜农要在AB上确定一个抽水点P ，使得抽水点P到两个菜园C ， D的距离和最短，则该最短距离为米．

（知识迁移）

借助上面的思考过程，请直接写出当0＜x＜15时，代数式 $\sqrt{x^{2} + 9} + \sqrt{{(15 - x)}^{2} + 25}$ 的最小值＝．

查看试题解析
24. 我们在学习二次根式时，了解了分母有理化及其应用．其实，还有一个类似的方法叫做“分子有理化”，即分母和分子都乘以分子的有理化因式，从而消除分子中的根式．
比如： $\sqrt{7} - \sqrt{6} = \frac{(\sqrt{7} - \sqrt{6}) (\sqrt{7} + \sqrt{6})}{\sqrt{7} + \sqrt{6}}$ ＝ $\frac{1}{\sqrt{7} + \sqrt{6}}$ ．

分子有理化可以用来比较某些二次根式的大小，也可以用来处理一些二次根式的最值问题．例如：比较： $\sqrt{7} - \sqrt{6}$ 和 $\sqrt{6} - \sqrt{5}$ 的大小可以先将它们分子有理化如下： $\sqrt{7} - \sqrt{6} = \frac{1}{\sqrt{7} + \sqrt{6}}$ ， $\sqrt{6} - \sqrt{5} = \frac{1}{\sqrt{6} + \sqrt{5}}$ ．

因为 $\sqrt{7} + \sqrt{6} > \sqrt{6} + \sqrt{5}$ ，所以， $\sqrt{7} - \sqrt{6} < \sqrt{6} - \sqrt{5}$ ．

再例如，求y＝ $\sqrt{x + 2} - \sqrt{x - 2}$ 的最大值、做法如下：

解：由x＋2≥0，x﹣2≥0可知x≥2，而y＝ $\sqrt{x + 2} - \sqrt{x - 2}$ ＝ $\frac{4}{\sqrt{x + 2} + \sqrt{x - 2}}$ ．当x＝2时，分母 $\sqrt{x + 2} + \sqrt{x - 2}$ 有最小值2.所以y的最大值是2

利用上面的方法，完成下面问题：

(1)、比较 $\sqrt{19}$ ﹣ $\sqrt{18}$ 和 $\sqrt{18}$ ﹣ $\sqrt{17}$ 的大小；

(2)、求y＝ $\sqrt{x + 1}$ ﹣ $\sqrt{x - 1}$ ＋2的最大值．

查看试题解析