山东省德州市乐陵市2021-2022学年八年级上学期期中数学试题

试卷更新日期：2021-12-06 类型：期中考试

进入出卷网下载

一、单选题

1. 第十四届全运会中，山东代表团以58枚金牌、55枚银牌、47枚铜牌，总计160枚奖牌的成绩锁定奖牌榜第一的位置，下列关于体育的图形中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 经常开窗通风，可以有效地利用阳光和空气中的紫外线杀死病菌，清除室内空气中的有害气体，净化空气，如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是（）

A、三角形的稳定性 B、两点之间线段最短 C、两点确定一条直线 D、垂线段最短

查看试题解析
3. 下列长度的三段钢条，不能组成一个三角形框架的是（）

A、 $2 cm$ ， $3 cm$ ， $4 cm$ B、 $3 cm$ ， $7 cm$ ， $7 cm$ C、 $2 cm$ ， $2 cm$ ， $6 cm$ D、 $5 cm$ ， $6 cm$ ， $7 cm$

查看试题解析
4. 将一张长方形纸对折，然后用笔尖在纸上扎出“B”，再把纸铺平，可以看到的是（）

A、 B、 C、 D、

查看试题解析
5. 一个正多边形的一个外角是 $40 °$ ，则该正多边形的内角和是（）

A、 $720 °$ B、 $900 °$ C、 $1085 °$ D、 $1260 °$

查看试题解析
6. 用三角板作△ABC的边BC上的高，下列三角板的摆放位置正确的是（　　）

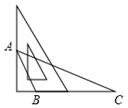A、 B、 C、 D、

查看试题解析
7. 若点A（1+m，1﹣n）与点B（﹣3，2）关于y轴对称，则m+n的值是（）

A、﹣5 B、﹣3 C、3 D、1

查看试题解析
8. 在联合会上，有A、B、C三名选手站在一个三角形的三个顶点位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置是在△ABC的（　　）

A、三边中线的交点 B、三条角平分线的交点 C、三边垂直平分线的交点 D、三边上高的交点

查看试题解析
9. 如图，已知 $∠ C A E = ∠ D A B$ ， $A C = A D$ ，增加哪个条件不能保证 $△ A B C ≌ △ A E D$ 的是（）

A、 $A B = A E$ B、 $B C = E D$ C、 $∠ C = ∠ D$ D、 $∠ B = ∠ E$

查看试题解析
10. 如图入口进入，沿框内问题的正确判断方向，最后到达的是（　　）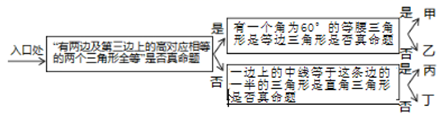

A、甲 B、乙 C、丙 D、丁

查看试题解析
11. 如图，已知钝角△ABC，依下列步骤尺规作图，并保留作图痕迹.
步骤1：以C为圆心，CA为半径画弧①；

步骤2：以B为圆心，BA为半径画弧②，交弧①于点D；

步骤3：连接AD，交BC延长线于H；

下列叙述正确的是（）

A、BH垂直平分线段AD B、AC平分∠BAD C、 $S_{△ A B C}$ =BC·AH D、BC=CH

查看试题解析
12. 如图，△ $A B C$ 中， $∠ A B C$ 、 $∠ E A C$ 的角平分线 $B P$ 、 $A P$ 交于点 $P$ ，延长 $B A$ 、 $B C$ ， $P M ⊥ B E$ ， $P N ⊥ B C$ ，则下列结论中正确的个数是（）
①CP平分∠ACF；②∠ABC+2∠APC=180°；③∠ACB=2∠APB④若PM⊥BE，PN⊥BC，则AM+CN=AC；

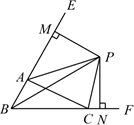A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 在三角形ABC中， $∠ A ： ∠ B ： ∠ C = 1 ： 2 ： 3$ ，则 $∠ C$ 的度数为．

查看试题解析
14. 如图， $△ A B C ≌ △ D C B$ ， $A C = 7$ ， $O B = 5$ ，则 $O A =$ ．

查看试题解析
15. 如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点 $C^{'}$ 处，折痕为EF，若∠ABE=20°，那么∠DEF的度数为.

查看试题解析
16. 小明在纸上面了一个边长为5cm的等边三角形 $△ A B C$ ，并将一个宽为2cm直尺如图所示放在所画 $△ A B C$ 上，使得直尺一条边与 $△ A B C$ 的边BC重合，另一条边交边AB于点E ，则AE= ．

查看试题解析
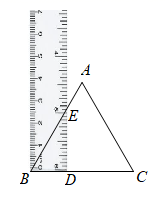17. 如图所示，在 $△ A B C$ 中， $A B = 3$ ， $A C = 4$ ，EF垂直平分BC ，交AC于点D ，交BC于点G ，点P为直线EF上一动点，则 $△ A B P$ 周长的最小值是．

查看试题解析
18. 在x轴，y轴上分别截取OA ， OB ，使 $O A = O B$ ，再分别以点A ， B为圆心，以大于 $\frac{1}{2} A B$ 长为半径画弧，两弧交于点P ．若点P的坐标为 $(a ， 2 a - 3)$ ，则a的值为．

查看试题解析

三、解答题

19. 如图，在平面直角坐标系中，已知 $Δ A B C$ 的三个顶点坐标分别是 $A (2 ， - 1) ， B (1 ， - 2) ， C (3 ， - 3)$

（ 1 ）将 $Δ A B C$ 向上平移4个单位长度得到 $Δ A_{1} B_{1} C_{1}$ ，请画出 $Δ A_{1} B_{1} C_{1}$ ；

（ 2 ）请画出与 $Δ A B C$ 关于 $y$ 轴对称的 $Δ A_{2} B_{2} C_{2}$ ；

（ 3 ）请写出 $A_{1} 、 A_{2}$ 的坐标．

查看试题解析
20. 某地地震过后，河沿村中学的同学用下面的方法检测教室的房梁是否水平；在等腰直角三角尺斜边中点拴一条线绳，线绳的另一端挂一个铅锤，把这块三角尺的斜边贴在房梁上，结果线绳经过三角尺的直角顶点，同学们由此确信房梁是水平的，他们的判断对吗？为什么？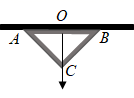

查看试题解析
21. 已知a、b、c是△ABC的三边长，a=4，b=6，设三角形的周长是x．

(1)、直接写出c及x的取值范围；

(2)、若x是小于18的偶数，①求c的长；
②判断△ABC的形状．

查看试题解析
22. 如图所示，点B ， E ， C ， F在同一条直线上，能否由 $A C = D E$ ， $B E = F C$ 来证明AC∥DE？如果能，请给出证明；如果不能，请从下列四个条件中再选择一个合适的条件，使AC∥DE成立，并说明理由．供选择的四个条件：① $∠ A = ∠ D$ ；② $A B = D F$ ；③AB∥DF；④ $∠ A = ∠ D = 90 °$ ．

查看试题解析
23. 尺规作图（不写作法，保留作图痕迹）
已知 $∠ A O B$ ，

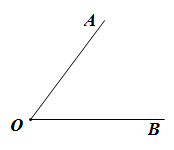(1)、作 $∠ A O B$ 的平分线；

(2)、作一个角等于 $∠ A O B$ ．

查看试题解析
24. 两个大小不同的等腰直角三角板如图所示放置，右图是由它抽象出的几何图形，B ， C ， E在同一条直线上，连接DC ．

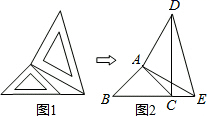(1)、求证：△ABE≌△ACD；

(2)、若图2中的BE＝3CE ， CD＝6，求 △DCE的面积．

查看试题解析
25. 如图，在 Rt△ABC 中，∠C＝90°，∠A＝60°，AB＝10cm ，若点M 从点 B 出发以 2cm/s 的速度向点 A 运动，点 N 从点 A 出发以 1cm/s 的速度向点 C 运动，设 M、N 分别从点 B、A 同时出发，运动的时间为 ts ．

(1)、用含 t 的式子表示线段 AM、AN 的长；

(2)、当 t 为何值时，△AMN 是以 MN 为底边的等腰三角形？

(3)、当 t 为何值时，MN∥BC？并求出此时 CN 的长．

查看试题解析