江西省南昌市2021-2022学年八年级上学期期中数学试题
试卷更新日期：2021-12-06 类型：期中考试
一、单选题
-
1. 下列疫情防控宣传图片中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 在△ABC中，∠A+∠B＝∠C ， 则△ABC为（ ）三角形．A、锐角 B、直角 C、钝角 D、无法确定3. 如图，AC⊥BE于点C，DF⊥BE于点F，BC＝EF，如果添加一个条件后，可以直接利用“HL”来证明△ABC≌△DEF，则这个条件应该是（ ）
A、AC=DE B、∠D=∠A C、AB=DE D、∠B=∠E4. 如图，在Rt△ABC中，∠ACB=90°，∠B=60°，CD是△ABC的高，且BD=2，则AD的长为（ ）
A、6 B、7 C、8 D、95. 已知点A（m ， 2021）与点B（2020，n）关于x轴对称，则m+n的值为（ ）A、1 B、﹣1 C、0 D、26. 如图“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC=CD=DE，点D、E可在槽中滑动，若∠BDE=72°，则∠CDE的度数是（ ）
A、63° B、65° C、75° D、84°二、填空题
-
7. 如图，点D为BC的延长线上一点，图中x的值为 ．
8. 如图中的两个三角形全等，图中的字母 ， ， 表示三角形的边长，则 的大小是.
9. 如图，在△ABC中，BD是边AC上的高，CE平分∠ACB，交BD于点E，DE＝2，BC＝5，则△BCE的面积为 ．
10. 正多边形的一个内角等于144°，则这个多边形的边数是 ．11. 如图，在△ABC中，AB＝AC ， 点D为BC边的中点，∠1＝25°，则∠C＝ ．
12. 在△ABC中，∠B＝80°，过点A作一条直线，将△ABC分成两个新的三角形，若这两个三角形都是等腰三角形，则∠C的度数为 ．三、解答题
-
13.(1)、如图1，在△ABC中，D是AB上一点，E是AC上一点，BE、CD相交于点F ， ∠A＝62°，∠ACD＝35°，∠ABE＝20°．求：∠BFD的度数．对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）．
解：∵∠BDC＝∠A+∠ACD（ ▲ ），
∴∠BDC＝62°+35°＝97°（等量代换）．
∵∠BFD+∠BDC+∠ABE＝ ▲ （ ▲ ），
∴∠BFD＝180°﹣∠BDC﹣∠ABE＝180°﹣97°﹣20°＝63°（等式的性质）．
(2)、如图2，把一个长方形的纸ABCD沿对角线折叠（长方形对边平行且相等，四个角是直角），重合部分△FBD是个什么三角形？请证明你的结论．14. 如示例图将4×4的棋盘沿格线划分成两个全等的图形，请再用另外3种方法将4×4的棋盘沿格线划分成两个全等图形（约定某两种划分法可经过旋转、轴对称得到的划分法为相同划分法）.
15. 如图，AD ， AE分别是△ABC的高和角平分线．
(1)、已知∠B＝40°，∠C＝60°，求∠DAE的度数；(2)、设∠B＝α，∠C＝β（α＜β）．请直接写出用α、β表示∠DAE的关系式 ．16. 如图， ， ，垂足分别为D，E，BE和CD相交于点O， ，连AO，
求证：
(1)、 ≌ ；(2)、 ．17. 如图，在△ABC中，AB＝AC ， DE垂直平分AB ， 交边AB于点D ， 交边AC于点E ， BF垂直平分CE ， 交AC于点F ， 连接BE ．
(1)、求证：AE＝BC；(2)、求∠A的度数．18. 我们经常遇到需要分类的问题，画“树形图”可以帮我们不重复、不遗漏地分类．（问题提出）
(1)、在等腰三角形ABC中，若∠A＝80°，根据下面分析、直接写出∠B的度数 ．分析：∠A、∠B都可能是顶角或底角，因此需要分成如图所示的3类，这样的图就是树形图．请根据此分析、求出∠B的度数．
(2)、（问题解决）已知等腰三角形ABC周长为19，AB＝7，仿照例题画出树形图，并求出BC的长度．
19. 如图1，为测量池塘宽度AB ， 可在池塘外的空地上取任意一点O ， 连接AO ， BO ， 并分别延长至点C ， D ， 使OC＝OA ， OD＝OB ， 连接CD ．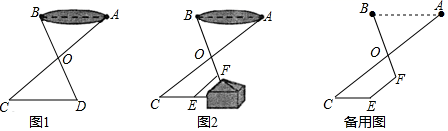
(1)、求证：AB＝CD；(2)、如图2，受地形条件的影响，于是采取以下措施：延长AO至点C ， 使OC＝OA ， 过点C作AB的平行线CE ， 延长BO至点F ， 连接EF ， 测得∠CEF＝140°，∠OFE＝110°，CE＝11m，EF＝10m，求出池塘AB的宽度．20. 在学习完第十二章后，刘老师让同学们独立完成识本56页第9题：如图1，∠ACB＝90°，AC＝BC ， AD⊥CE ， BE⊥CE ， 垂足分别为D ， E ． AD＝2.5cm，DE＝1.7cm，求BE的长．
(1)、请你也独立完成这道题；(2)、待同学们完成这道题后，刘老师又出示了一道题：在课本原题其它条件不变的前提下，将CE所在直线旋转到△ABC的外部（如图2），请你猜想AD ， DE ， BE三者之间的数量关系，直接写出结论，不需证明．(3)、如图3，将（1）中的条件改为：在△ABC中，AC＝BC ， D ， C ， E三点在同一条直线上，并且有∠BEC＝∠ADC＝∠BCA＝α，其中α为任意纯角，那么（2）中你的猜想是否还成立？若成立，请证明；若不成立，请说明理由．21.
(1)、我们已经知道，在 中，如果 ，则 ，下面我们继续研究：如图①，在 中，如果 ，则 与 的大小关系如何？为此，我们把 沿 的平分线翻折，因为 ，所以点 落在 边的点 处，如图②所示，然后把纸展平，连接 ，接下来，你能推出 与 的大小关系了吗？试写出说理过程.(2)、如图③，在 中， 是角平分线，且 ，求证： .(3)、在（2）的条件下，若点 、 分别为 、 上的动点，且 ， ，则 的最小值为.