江西省吉安市2021-2022学年八年级上学期期中数学试题

试卷更新日期：2021-12-06 类型：期中考试

进入出卷网下载

一、单选题

1. 在7个实数 $- \frac{22}{7}$ ， $\sqrt{5}$ ，0， $\sqrt[3]{8}$ ， $- π$ ， $\sqrt{64}$ ，1.101001000100001中，无理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列各式中，是最简二次根式的是（）

A、 $\sqrt[3]{2}$ B、 $\sqrt{5}$ C、 $\sqrt{8}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
3. 下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（　　）

A、 $\sqrt{3}$ ，2， $\sqrt{5}$ B、2，3，4 C、1， $\sqrt{2}$ ， $\sqrt{3}$ D、 $\frac{1}{3}$ ， $\frac{1}{4}$ ， $\frac{1}{5}$

查看试题解析
4. 将直线 $y = - 2 x - 1$ 向下平移两个单位，平移后的直线所对应的函数关系式为（）

A、 $y = - 2 x - 5$ B、 $y = - 2 x - 3$ C、 $y = - 2 x + 1$ D、 $y = - 2 x + 3$

查看试题解析
5. 在平面直角坐标系中，点A（2，m）和点B（n ， 3）关于 $x$ 轴对称，则 $\sqrt{{(m + n)}^{2}}$ 的值为（）

A、5 B、﹣5 C、1 D、﹣1

查看试题解析
6. 对于函数 $y = - 2 x + 2$ ，下列结论正确的是（）

A、它的图象必经过点 $(- 1 ， 0)$ B、它的图象经过第二、三、四象限 C、 $y$ 的值随 $x$ 值的增大而增大 D、当 $x > 1$ 时， $y < 0$

查看试题解析

二、填空题

7. $\sqrt{{(- 5)}^{2}}$ 的平方根是．

查看试题解析
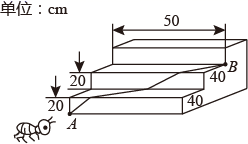
8. 点 $(3 + a ， 5)$ 关于 $y$ 轴对称的点的坐标是 $(- 5 ， 4 - b)$ ，则 $b^{a} =$ ．

查看试题解析
9. 若实数 $x ， y$ 满足 ${(2 x - 3)}^{2} + | 9 + 4 y | = 0$ ，则 $x y$ 的立方根为．

查看试题解析
10. 已知一次函数y＝（m﹣1）x+m²﹣1的图象经过原点，那么m＝．

查看试题解析
11. 如图，台阶阶梯每一层高 $20 cm$ ，宽 $40 cm$ ，长 $50 cm$ ．一只蚂蚁从 $A$ 点爬到 $B$ 点，最短路程是．

查看试题解析
12. 已知在 $Rt △ A B C$ 中， $A B = A C = 2$ ， $∠ B A C = 90 °$ ，以 $A C$ 为一边在 $Rt △ A B C$ 外部作等腰直角三角形 $A C D$ ，线段 $B D$ 的长为．

查看试题解析

三、解答题

13.

(1)、计算： $\sqrt{8} - | - \sqrt{2} | + {(- 2 \sqrt{3})}^{2} - {(π - 3.14)}^{0} \times {(\frac{1}{2})}^{- 2}$ ；

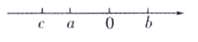
(2)、解方程： $- 8 {(x + 1)}^{3} = 27$ ．

查看试题解析
14. 已知 x+3 的立方根为 2，3x+y-1 的平方根为±4 ，求 3x+5y 的算术平方根．

查看试题解析
15. 已知实数a，b，c在数轴上的位置如图所示，化简： $| a | - \sqrt{{(a + c)}^{2}} + \sqrt{{(c - a)}^{2}} - \sqrt{b^{2}}$ .

查看试题解析
16. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点就做格点，以格点为顶点分别按下列要求画出图形．

(1)、在图1中画一个三角形，使得该三角形的三边长分别为5， $\sqrt{5}$ ， $2 \sqrt{5}$ ；

(2)、在图2中画出一个正方形，使得该正方形的面积为10．

查看试题解析
17. 铁路上A、B两站（视为直线上的两点）相距25km ， C ， D为两村庄（视为两个点）， $D A ⊥ A B$ 于点A ， $C B ⊥ A B$ 于点B（如图）．已知 $D A = 10 km$ ， $C B = 15 km$ ，现在要在铁路AB上建一个土特产收购站E ，使得C ， D两村庄到收购站E的直线距离相等，请求出收购站E到A站的距离．

查看试题解析
18. 已知 $y + 2$ 与 $x - 1$ 成正比例，且当 $x = 3$ 时， $y = 4$ ．

(1)、求 $y$ 与 $x$ 之间的函数表达式；

(2)、当 $y = 1$ 时，求 $x$ 的值．

查看试题解析
19. 如图， $△ A B C$ 三个顶点的坐标分别为 $A (- 5 ， 4)$ 、 $B (- 2 ， 2)$ 、 $C (- 4 ， 1)$ ．

(1)、若 $△ A_{1} B_{1} C_{1}$ 与 $△ A B C$ 关于 $y$ 轴成轴对称，请在答题卷上作出 $△ A_{1} B_{1} C_{1}$ ，并写出 $△ A_{1} B_{1} C_{1}$ 的三个顶点坐标；

(2)、求 $△ A_{1} B_{1} C_{1}$ 的面积；

(3)、若点 $P$ 为 $y$ 轴上一点，要使 $C P + B P$ 的值最小，请在答题卷上作出点 $P$ 的位置．（保留作图痕迹）

查看试题解析
20. 阅读材料：像 $(\sqrt{5} + 2) (\sqrt{5} - 2) = 1$ ， $\sqrt{a} \times \sqrt{a} = a (a \geq 0)$ ……这种两个含二次根式的代数式相乘，积不含二次根式，我们称这两个代数式互为有理化因式．在进行二次根式运算时，利用有理化因式可以化去分母中的根号．
例如： $\frac{1}{2 \sqrt{3}} = \frac{\sqrt{3}}{2 \sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{6}$ ； $\frac{\sqrt{2} + 1}{\sqrt{2} - 1} = \frac{{(\sqrt{2} + 1)}^{2}}{(\sqrt{2} - 1) (\sqrt{2} + 1)} = 3 + 2 \sqrt{2}$ ．

解答下列问题：

(1)、 $\sqrt{7}$ 的有理化因式是； $\sqrt{5} + 2$ 的有理化因式是；

(2)、观察下面的变形规律，请你猜想： $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ ．
$\frac{1}{\sqrt{2} + 1} = \sqrt{2} - 1$ ， $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ ， $\frac{1}{\sqrt{4} + \sqrt{3}} = \sqrt{4} - \sqrt{3}$ …

(3)、利用上面的方法，请化简：
$\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + \cdot \cdot \cdot + \frac{1}{\sqrt{2020} + \sqrt{2021}}$

查看试题解析
21. 如图， $P$ 为等边三角形 $Δ A B C$ 内一点，分别连接 $P A ， P B ， P C$ ， $P A = 6 ， P B = 8 ， P C = 10$ ．以 $P A$ 为边作等边三角形 $Δ A P D$ ，连接 $B D$ ．

(1)、求证： $B D = P C$ ．

(2)、求 $∠ A P B$ 的度数．

查看试题解析
22. 如图，C为线段BD上一动点，分别过点B、D作 $A B ⊥ B D$ ， $E D ⊥ B D$ ，连接AC、EC ．已知 $A B = 3$ ， $D E = 2$ ， $B D = 12$ ，设 $C D = x$ ．

(1)、用含x的代数式表示 $A C + C E$ 的长．

(2)、请问点C满足什么条件时， $A C + C E$ 的值最小，并求出此时 $A C + C E$ 的最小值．

(3)、根据（2）中的规律和结论，重新构图求出代数式 $\sqrt{x^{2} + 1} + \sqrt{{(8 - x)}^{2} + 25}$ 的最小值．

查看试题解析
23. 如图，直线y＝kx﹣2与x轴，y轴分别交于B ， C两点，其中OB＝1．

(1)、求k的值；

(2)、若点A（x ， y）是第一象限内的直线y＝kx﹣2上的一个动点，当点A运动过程中，试写出△AOB的面积S与x的函数关系式；

(3)、在（2）的条件下，探索：
①当点A运动到什么位置时，△AOB的面积是1；

②在①成立的情况下，x轴上是否存在一点P ，使△POA是等腰三角形？若存在，请写出满足条件的所有P点的坐标；若不存在，请说明理由．

查看试题解析