河北省邯郸市永年区2021-2022学年八年级上学期期中考试数学试题

试卷更新日期：2021-12-06 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列各数： $0.51525354$ …、 $\sqrt{\frac{49}{100}}$ 、 $0. \dot{2}$ 、 $\frac{1}{π}$ 、 $\frac{131}{11}$ 、 $\sqrt[3]{27}$ 、 $8.032032032$ …中，无理数的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
2. 关于分式 $\frac{x - 7}{{(x + 1)}^{2}}$ ，下列说法错误的是（）

A、当 $x = - 1$ 时，分式没有意义 B、当 $x > 7$ 时，分式的值为正数 C、当 $x < 7$ 时，分式的值为负数 D、当 $x = 7$ 时，分式的值为零

查看试题解析
3. 以下命题的逆命题为真命题的是（）

A、邻补角相等 B、同旁内角互补，两直线平行 C、若 $a = b$ ，则 $a^{2} = b^{2}$ D、若 $a > 0 ， b > 0$ ，则 $a^{2} + b^{2} > 0$

查看试题解析
4. 下列变形错误的是（）

A、 $\frac{x - y}{x^{2} - y^{2}} = \frac{1}{x + y}$ B、 $\frac{3 x y}{- x^{2} y} = \frac{3}{x}$ C、 $\frac{- x + y}{2} = - \frac{x - y}{2}$ D、 $\frac{2 a + 2 b}{3 a^{2} + 6 a b + 3 b^{2}} = \frac{2}{3 (a + b)}$

查看试题解析
5. 下列对近似数的叙述错误的是（）

A、用四舍五入法对270.18（精确到个位）取近似值为270 B、用四舍五入法对0.518（精确到0.01）取近似值为0.52 C、由四舍五入法得到的近似数42.3万是精确到万位 D、由四舍五入法得到的近似数0.185是精确到千分位

查看试题解析
6. 嘉淇在用直尺和圆规作一个角等于已知角的步骤如下：
已知：∠AOB ．

求作：∠A'O'B'，使∠A'O'B'=∠AOB ．

作法：

⑴如图，以点O为圆心，m为半径画弧，分别交OA ， OB于点C ， D；

⑵画一条射线O'A'，以点O'为圆心，n为半径画弧，交O'A'于点C'；

⑶以点C'为圆心，p为半径画弧，与第（2）步中所画的弧相交于点D'；

⑷过点D'画射线O'B'，则∠A'O'B'=∠AOB ．

下列说法正确的是（）

A、m－p>0 B、1－p>0 C、p= $\frac{1}{2}$ n>0 D、m=n>0

查看试题解析
7. 解分式方程 $\frac{x - 8}{x - 7} - \frac{5 x}{14 - 2 x} = 8$ 时，去分母后得到的整式方程是（）

A、2（x－8）＋5x＝16（x－7） B、2（x－8）＋5x＝8 C、2（x－8）－5x＝16（x－7） D、2（x－8）－5x＝8

查看试题解析
8. $- 27$ 的立方根与 $\sqrt{81}$ 的平方根之和是（）．

A、6或 $- 6$ B、0或 $- 6$ C、6或 $- 12$ D、0或6

查看试题解析
9. 如图，在 $△ A B C$ 中，D ， E分别是边 $A C$ ， $B C$ 上的点，若 $△ A D B ≌ △ E D B ≌ △ E D C$ ，则 $∠ C$ 的度数为（）

A、 $15 °$ B、 $20 °$ C、 $25 °$ D、 $30 °$

查看试题解析
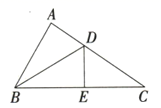10. 当 $a = 2 - b$ 时，计算 $(a - \frac{b^{2}}{a}) \div \frac{a - b}{a}$ 的值为（）

A、2 B、-2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
11. 下列各式中，正确的是（）

A、 $\sqrt{36} = \pm 6$ B、 $\pm \sqrt{25} = \pm 5$ C、 $\sqrt{{(- 2)}^{2}} = - 2$ D、 $\sqrt[3]{- 27} = 3$

查看试题解析
12. 如图， $A B = D B ， ∠ 1 = ∠ 2$ ，欲证 $△ A B E ≌ △ D B C$ ，则补充的条件中错误的是（）

A、 $∠ A = ∠ D$ B、 $∠ E = ∠ C$ C、 $∠ A = ∠ C$ D、 $B C = B E$

查看试题解析
13. 比较大小错误的是（）

A、 $\sqrt{5}$ ＜ $\sqrt{7}$ B、 $\sqrt{35}$ ＋2＜ $\sqrt{82}$ ﹣1 C、 $\frac{- 7 - \sqrt{23}}{2}$ ＞﹣6 D、|1－ $\sqrt{3}$ |＞ $\sqrt{3}$ －1

查看试题解析
14. 某次列车平均提速v km/h，用相同的时间，列车提速前行驶s km，提速后比提速前多行驶50km，则方程 $\frac{s}{x} + v = \frac{s + 50}{x}$ 所表达的等量关系是（）

A、提速前列车行驶s km与提速后行驶(s＋50)km的时间相等 B、提速后列车每小时比提速前列车每小时多开v km C、提速后列车行驶(s＋50)km的时间比提速前列车行驶s km多v h D、提速后列车用相同的时间可以比提速前多开50km

查看试题解析
15. 如图， $O A = O B ， O C = O D ， ∠ O = 60 ° ， ∠ C = 25 °$ ，则 $∠ B E D$ 等于（）

A、 $70 °$ B、 $60 °$ C、 $50 °$ D、 $40 °$

查看试题解析
16. 若关于 $x$ 的不等式组 ${\begin{array}{l} \frac{3 x}{2} - 1 \geq \frac{x + 4}{2} \\ a - x > 7 \end{array}$ 无解，且关于 $y$ 的分式方程 $\frac{3 y}{2 - y} = 1 - \frac{a + y}{y - 2}$ 的解为非负整数，则符合条件的所有整数 $a$ 的和为（　　）

A、6 B、16 C、18 D、20

查看试题解析

二、填空题

17. 关于 $x$ 的分式方程 $\frac{m}{x - 2} + \frac{3}{2 - x} = 1$ 有增根，则 $m$ 的值为．

查看试题解析
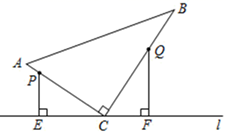
18. 已知 $\sqrt{a^{3} - 64} + | b^{3} + 27 | = 0$ ，则 $a + b$ 的平方根是．

查看试题解析
19. 对于代数式 $M : (1 + \frac{m}{a - 1}) \div \frac{2 a}{a^{2} - 1}$ ，（m为整式）．

(1)、当 $m = a + 1$ 时，化简 $M$ 的结果为；

(2)、若化简M的结果为 $\frac{a + 1}{2}$ ，则 $m =$ ．

查看试题解析
20. 如图，在△ABC中，∠ACB=90，AC=6，BC=8.点P从点A出发，沿折线AC—CB以每秒1个单位长度的速度向终点B运动，点Q从点B出发沿折线BC—CA以每秒3个单位长度的速度向终点A运动，P、Q两点同时出发.分别过P、Q两点作PE⊥l于E，QF⊥l于F，当△PEC与△QFC全等时，CQ的长为.

查看试题解析

三、解答题

21. 已知实数 $2 x + 1$ 和 $x - 7$ 是正数 $a$ 的两个不同的平方根．

(1)、求 $x$ 和的值．

(2)、求 $2 - 5 x$ 的立方根．

查看试题解析
22. 解分式方程：

(1)、 $\frac{2}{x - 1} - \frac{3}{x + 1} = \frac{x - 3}{x^{2} - 1}$

(2)、 $\frac{x}{x - 2} - 1 = \frac{8}{x^{2} - 4}$

查看试题解析
23. 如图，点E在AB上，△ABC≌△DEC，求证：CE平分∠BED．

查看试题解析
24. 我们知道， $\sqrt{2}$ 是一个无理数，将这个数减去整数部分，差就是小数部分，即 $\sqrt{2}$ 的整数部分是1，小数部分是 $\sqrt{2} - 1$ ，请回答以下问题：

(1)、 $\sqrt{10}$ 的小数部分是， $\sqrt{17} -2$ 的小数部分是；

(2)、若 $a$ 是 $\sqrt{90}$ 的整数部分， $b$ 是 $\sqrt{3}$ 的小数部分，求 $a + b - \sqrt{3}$ 的立方根．

查看试题解析
25. 某工程公司承包了修筑一段塌方道路的工程，并派旗下第五、六两个施工队前去修筑，要求在规定时间内完成．

(1)、已知第五施工队单独完成这项工程所需时间比规定时间多32天，第六施工队单独完成这项工程所需时间比规定时间多12天，如果第五、六施工队先合作20天，剩下的由第五施工队单独施工，则要误期2天完成那么规定时间是多少天？

(2)、实际上，在第五、六施工队合作完成这项工程的 $\frac{5}{6}$ 时，公司又承包了更大的工程，需要调走一个施工队．你认为留下哪个施工队继续施工能按时完成剩下的工程？

查看试题解析
26. （教材呈现）如图是华师版八年级上册数学教材第69页的部分内容：
如图，在 $△ A B C$ 中，D是边BC的中点，过点C画直线CE ，使 $C E // A B$ ，交AD的延长线于点E ，求证： $A D = E D$

证明∵ $C E // A B$ （已知）

∴ $∠ A B D = ∠ E C D$ ， $∠ B A D = ∠ C E D$ （两直线平行，内错角相等）．

在 $△ A B D$ 与 $△ E C D$ 中，

∵ $∠ A B D = ∠ E C D$ ， $∠ B A D = ∠ C E D$ （已证），

$B D = C D$ （已知），

∴ $△ A B D ≌ △ E C D (A .A .S)$ ，

∴ $A D = E D$ （全等三角形的对应边相等）．

(1)、（方法应用）如图①，在 $△ A B C$ 中， $A B = 6$ ， $A C = 4$ ，则BC边上的中线AD长度的取值范围是．

(2)、（猜想证明）如图②，在四边形ABCD中， $A B // C D$ ，点E是BC的中点，若AE是 $∠ B A D$ 的平分线，试猜想线段AB、AD、DC之间的数量关系，并证明你的猜想；

(3)、（拓展延伸）如图③，已知 $A B // C F$ ，点E是BC的中点，点D在线段AE上， $∠ E D F = ∠ B A E$ ，若 $A B = 5$ ， $C F = 2$ ，求出线段DF的长．

查看试题解析