广东省珠海市香洲区2021-2022学年八年级上学期期中数学试题
试卷更新日期：2021-12-06 类型：期中考试
一、单选题
-
1. 下列平面图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 一个三角形的两边长为3和8，第三边长为奇数，则第三边长为（ ）A、5或7 B、7或9 C、7 D、93. 如图，已知AB＝DC ， AD＝BC ， E ， F在DB上两点且BF＝DE ， 若∠AEB＝120°，∠ADB＝30°，则∠BCF＝ （ ）
A、150° B、40° C、80° D、90°4. 如图，DE是△ABC中AC边上的垂直平分线，如果BC＝8cm ， AB＝10cm ， 则△EBC的周长为（ ）
A、16cm B、18cm C、26cm D、28cm5. 如图，在△ABC中，ED⊥BC ， EA⊥AB ， 若△EAB≌△EDB≌△EDC ， 则∠C＝（ ）
A、36° B、30° C、25° D、15°6. 如图，AE＝AF ， AB＝AC ， EC与BF交于点O ， ∠A＝60°，∠B＝25°，则∠EOB的度数为（ ）
A、60° B、70° C、75° D、15°7. 已知等腰三角形其中一个内角为70°，那么这个等腰三角形的顶角度数为（ ）A、70° B、70°或55° C、40°或55° D、70°或40°8. 下图中显示的是从镜子中看到的背后墙上电子钟的读数，由此你可以推断这时的实际时间是（ ）
A、10：05 B、20：01 C、20：10 D、10：029.如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带（ ）去.
A、① B、② C、③ D、①和②10. 如图，△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB ， PS⊥AC ， 垂足分别是R、S ， 若AQ=PQ ， PR=PS ， 下面四个结论：①AS=AR；②QP∥AR；③△BRP≌△QSP；④AP垂直平分RS ． 其中符合题意结论的序号是（ ）．
A、①② B、①②③ C、①②④ D、①②③④二、填空题
-
11. 在△ABC中，∠A：∠B：∠C=2：3：4，则∠A= ， ∠C= ．12. 若正多边形的每一个内角为 ，则这个正多边形的边数是 ．13. 已知，点A（m﹣1，3）与点B（2，n﹣1）关于x轴对称，则（m+n）2020的值为 ．14. 如图，已知方格纸中是4个相同的小正方形，则 的度数为.
15. 如图，在△ABC和△FDE中，AD=FC ， AB=EF ， 当添加条件时，就可得到△ABC≌△FED ． （只需填写一个正确条件即可）
16. 如图，在△ABC中，AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于点D，则∠DBC＝度.
17. 已知：如图，∠AOB＝45°，点P为∠AOB内部的点，点P关于OB ， OA的对称点P1 ， P2的连线交OA ， OB于M ， N两点，连接PM ， PN ， 若OP＝2，则△PMN的周长＝ ．
18. 一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数．三、解答题
-
19.
如图，已知点B、E、C、F在同一直线上，AB=DE，∠A=∠D，AC∥DF．
求证：
(1)、△ABC≌△DEF；
(2)、BE=CF
20. 如图，在平面直角坐标系中，已知A（1，2），B（3，1），C（﹣2，﹣1）．
(1)、在图中作出△ABC关于y轴对称的△A1B1C1；(2)、写出点C1的坐标：；(3)、△A1B1C1的面积是多少？21. 如图，在△ABC中，∠B=∠C ， 点D、E、F分别在AB、BC、AC边上，且BE=CF ， AD+EC=AB ．
(1)、求证：DE=EF；(2)、当∠A=36°时，求∠DEF的度数．22. 如图所示，在四边形ABCD中，AD//BC ， E为CD的中点，连接AE、BE ， 且BE⊥AE ， 延长AE交BC的延长线于点F ． 求证：
(1)、AB＝BC+AD ．(2)、AE平分∠BAD ．23. 如图，AD为△ABC的中线，BE为△ABD的中线．
(1)、∠ABE＝15°，∠BAD＝40°，求∠BED的度数；(2)、尺规作图：过点E作EF⊥BC ， 垂足为F（保留作图痕迹）；(3)、在（2）的条件下，若△ABC的面积为40，BC＝10，求EF的长．24. 如图，已知△ABC和△CDE均为等边三角形，且点B、C、D在同一条直线上，连接AD、BE ， 交CE和AC分别于G、H点，连接GH ．
(1)、求证：AD＝BE；(2)、求证：△BCH≌△ACG；(3)、试猜想：△CGH是什么特殊的三角形，并加以说明．25. 如图，在等边△ABC中，AB＝9cm，点P从点C出发沿CB边向点B以2cm/s的速度移动，点Q从B点出发沿BA边向A点以5cm/s速度移动．Q两点同时出发，它们移动的时间为t秒钟．
(1)、你能用t表示BP和BQ的长度吗？请你表示出来．(2)、请问几秒钟后，△PBQ为等边三角形？(3)、若P、Q两点分别从C ． B两点同时出发，并且都按顺时针方向沿AEC三边运动，请问经过几秒钟后点P与点Q第一次在△ABC的哪条边上相遇？．26. 如图，等边△ABC中，A ， B关于y轴对称，AD⊥AC交y轴负半轴于点D ， C（0，6）．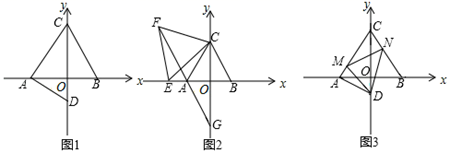
(1)、如图1，求D点坐标；(2)、如图2，E为x轴负半轴上任一点，以CE为边作等边△CEF ， FA的延长线交y轴于点G ， 求OG的长；(3)、如图3，在（1）的条件下，以D为顶点作60°的角，它的两边分别与CA、BC交于点MN ， 连接MN ． 探究线段AM、MN、NB之间的关系，并予以证明．