广东省东莞市2021-2022学年八年级上学期期中数学试题
试卷更新日期：2021-12-06 类型：期中考试
一、单选题
-
1. 下面四个图形是轴对称图形的是（ ）A、
B、
C、
D、
2. 由下列长度的三条线段，能组成一个三角形的是（ ）A、 B、 C、 D、3. 如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（ ）A、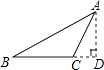
B、
C、
D、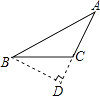
4. 下列设计的原理不是利用三角形的稳定性的是（ ）A、由四边形组成的伸缩门 B、自行车的三角形车架 C、斜钉一根木条的长方形窗框 D、照相机的三脚架5. 如图，在△ABC和△DEC中，已知AB＝DE ， ∠B＝∠E ， 还需添加一个条件才能使△ABC≌△DEC ， 则不能添加的一组条件是（ ）
A、BC＝EC B、∠ACD＝∠BCE C、∠A＝∠D D、AC＝DC6. 如图，△ABC与△DEF关于直线1对称，BE交l于点O ， 则下列说法不一定正确的是（ ）
A、AC＝DF B、BO＝EO C、AB＝EF D、l是线段AD的垂直平分线7. 用直尺和圆规作一个角等于已知角的示意图如图所示，则说明∠A′O′B′= ∠AOB 的依据是（ ）
A、SSS B、SAS C、ASA D、AAS8. 适合条件∠A＝ ∠B＝ ∠C的△ABC是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形9. 小张在操场从原地右转40°前行至十米的地方，再右转40°前行十米处，继续此规则前行，问小张第一次回到原地时，共走了（ ）米．A、70米 B、80米 C、90米 D、100米10. 如图，把△ABC纸片沿DE折叠，当点C落在四边形ABDE的外部时，测得∠1＝108°，∠C＝35°，则∠2的度数为（ ）
A、35° B、36° C、37° D、38°二、填空题
-
11. 在平面直角坐标系中，点P(1，2）关于y轴的对称点Q的坐标是；12. 某个正多边形有一个外角是36°，则这个正多边形是 边形.13. 若等腰三角形的一边长等于 ，另一边长等于 ，则它的周长等于.14. 如果将一副三角板按如图方式叠放，那么∠1的大小为 ．
15. 如图，已知∠ACB＝90°，OA平分∠BAC ， OB平分∠ABC ， 则∠AOB＝°．
16. 如图，五边形 中， ，则 的度数为 ．
17. 如图，已知AD BC ， ∠BAD与∠ABC的平分线相交于点P ， 过点P作EF⊥AD ， 交AD于点E ， 交BC于点F ， EF＝4cm，AB＝5cm，则△APB的面积为cm2
三、解答题
-
18. 如图，△ABC的各顶点坐标分别为A（4，﹣4），B（1，﹣1），C（3，﹣1）．
(1)、画出△ABC关于x轴对称的△A1B1C1；(2)、求△ABC的面积．19. 如图，AD是△ABC的角平分线，CE是△ABC的高，∠BAC＝60°，∠BCE＝40°，求∠ADC的度数．
20. 如图，点E、F在BC上，BE＝FC ， AB＝DC ， ∠A＝∠D＝90°．求证：∠B＝∠C ．
21. 用一条长为20cm的细绳围成一个等腰三角形(1)、如果腰长是底边长的2倍，那么各边的长是多少？(2)、能围成有一边长为5cm的等腰三角形吗？如果能，请求出它的另两边.22. 尺规作图，如图，已知三角形△ABC ．
(1)、尺规作图，作BC的垂直平分线DE ， 分别交AB于D、交BC于E（不要求写作法，保留作图痕迹）(2)、连结CD ， 若BE＝5，△ACD的周长为12，求△ABC的周长．23. 如图，AD与BC相交于点O ， OA＝OC ， ∠A＝∠C ．
(1)、求证：AB＝CD；(2)、若OE平分∠BOD ， 求证：OE垂直平分BD ．24. 如图1，∠ACB＝90°，AC＝BC ， AD⊥CE ， BE⊥CE ， 垂足分别为D ， E ．
(1)、求证：△CEB≌△ADC；(2)、若AD＝2.5cm，DE＝1.7cm，求BE的长；(3)、若将CE所在直线旋转到△ABC的外部（如图2），请你直接写出AD ， DE ， BE三者之间的数量关系是 ．25. 如图1，在△ABC中，若AB＝10，BC＝8，求AC边上的中线BD的取值范围．
(1)、小聪同学是这样思考的：延长BD至E ， 使DE＝BD ， 连接CE ， 可证得△CED≌△ABD ．①请证明△CED≌△ABD；
②中线BD的取值范围是 ▲ ．
(2)、问题拓展：如图2，在△ABC中，点D是AC的中点，分别以AB ， BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN ， 其中，AB＝BM ， BC＝BN ， ∠ABM＝∠NBC＝∠90°，连接MN ． 请写出BD与MN的数量关系，并说明理由．