广东省深圳市宝安区2021-2022学年第一学期九年级数学期中试卷

试卷更新日期：2021-12-06 类型：期中考试

进入出卷网下载

一、选择题

1. 若x²=9，则x=（）

A、3 B、-3 C、±3 D、81

查看试题解析
2. 如图，几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
3. 如图是一个可自由转动的游戏转盘，当转盘停止转动后(不考虑指针压线情况)，指针落在数字“Ⅱ”所示区域内的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

查看试题解析
4. 如图，三条直线a∥b∥c，若 $\frac{A D}{D F} = \frac{2}{3}$ ；则 $\frac{E C}{B C}$ =（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $\frac{2}{5}$ D、 $\frac{3}{5}$

查看试题解析
5. 用配方法解方程x²-6x-1=0时，配方结果正确的是（）

A、(x-3)²=10 B、(x-3)²=8 C、(x-6)²=10 D、(x-3)²=1

查看试题解析
6. 如图，已知△ABC与△DEF位似，位似中心为点O，△ABC的面积与△DEF面积之比为16：9，则CO：OF的值为（）

A、3：4 B、4：7 C、4：3 D、7：4

查看试题解析
7. 下列命题中，不正确的是( )

A、顺次连结菱形各边中点所得的四边形是矩形 B、有一个角是直角的菱形是正方形 C、对角线相等且垂直的四边形是正方形 D、有一个角是60°的等腰三角形是等边三角形

查看试题解析
8. 已知一次函数y₁=kx-b 与反比例函数y₂= $\frac{k}{x}$ ，在同一平面直角坐标系中的图象如图所示，则当kx< $\frac{k}{x}$ +b时，x的取值范围是（）

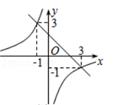A、x<-1或0<x<3 B、-1<x<0或x>3 C、-3<x<0或x> 1 D、x>3

查看试题解析
9. 如图，在 $▱$ ABCD中，点E在线段AB上，点F、G分别为对角线AC与DE、DB的交点．若AB：AE=3：2，则四边形BGFE与 $▱$ ABCD的面积之比为（）

A、7：60 B、8：70 C、5：43 D、3：26

查看试题解析
10. 如图，在Rt△ABC中，∠ACB=90°，AC=3，∠BAC=30°，把Rt△ABC沿AB翻折得到Rt△ABD，过点B作BE⊥BC，交AD于点E，点F是线段BE上一点，且∠ADF=45°．则下列结论：①AE=BE；②△BED∽△ABC；③BD²=AD·DE；④AF= $\sqrt{6}$ ，其中正确的有（）

A、①④ B、②③④ C、①②③ D、①②③④

查看试题解析

二、填空题

11. 若 $\frac{y}{x} = \frac{2}{3}$ ，则 $\frac{x + y}{y}$ =

查看试题解析
12. 如图，AB和DE是直立在地面上的两根立柱，AB=4m，AB在阳光下的影长BC=3m，在同一时刻阳光下DE的影长EF=4m，则DE的长为米．

查看试题解析
13. 在一个不透明的盒子中装有黑球和白球共200个，这些球除颜色外其余均相同，将球搅匀后任意摸出一个球，记下颜色后放回，通过大量重复摸球试验后，发现摸到白球的频率稳定在0.2，则盒子中白球有个．

查看试题解析
14. 如图，矩形△ABC的两边OA、OC分别在x轴和y轴上，以AC为边作平行四边形ACDE，E点在CB的延长线上，反比例函数y= $\frac{k}{x}$ (x>0)过B点且与CD交于F点，CF=3DF，S_△ABF=6，则k的值为

查看试题解析
15. 如图，在△ABC中，AC>AB，AD是角平分线，AE是中线，BF⊥AD于点G，交AE于点F，交AC于点M， EG的延长线交AB于点H，若∠BAC=60°，则 $\frac{F G}{D G}$ =

查看试题解析

三、解答题

16. 解方程：(x-3)²=2x(x-3)

查看试题解析
17. 先化简，再求值： $(\frac{x - 1}{x} - \frac{x - 2}{x + 1}) \div \frac{2 x^{2} - x}{x^{2} + 2 x + 1}$ ，其中x满足x²－2x－2=0.

查看试题解析
18. 在一个不透明的盒子中，共有“一白三黑”4颗围棋子，它们除了颜色之外没有其他区别．

(1)、随机地从盒中提出1颗棋子，则提出黑子的概率是多少

(2)、随机地从盒中同时提出2颗棋子，请你用画树状图或列表的方法表示所有等可能的结果，并求恰好提出“一黑一白"2颗棋子的概率．

查看试题解析
19. 如图，已知菱形ABCD，点E、F是对角线BD所在直线上的两点，且∠AED=45°，DF=BE，连接CE、AF、CF，得四边形AECF．

(1)、求证四边形AECF是正方形；

(2)、若BD=4，BE=3，求菱形ABCD的面积．

查看试题解析
20. 某公司展销如图所示的长方形工艺品，该工艺品长60cm，宽40cm，中间镶有宽度相同的三条丝绸花边．

(1)、若丝绸花边的面积为650cm² ，求丝绸花边的宽度；

(2)、已知该工艺品的成本是40元/件，如果以单价100元/件销售，那么每天可售出200件，另每天除工艺品的成本外所需支付的各种费用共2000元，根据销售经验，如果将销售单价每降低1元，每天可多售出20件，请问该公司每天所获利润能否达到22500元，如果能，应该把销售单价定为多少元？如果不能，请说明理由．

查看试题解析
21.

(1)、[证明体验]
如图13-1，AD为△ABC的角平分线，∠ADC=60°，点E在AB上，AE=AC．求证：DE平分∠ADB．

(2)、[思考探究]
如图13-2，在(1)的条件下，F为AB上一点，连结FC交AD于点G．若FB=FC，DG=2，CD=3，求BD的长．

(3)、[拓展延伸]
如图13-3，在四边形ABCD中，对角线AC平分∠BAD，∠BCA=2∠DCA，点E在AC上，∠EDC=∠ABC．若BC=5，CD=2 $\sqrt{5}$ ，AD=2AE，求AC的长．

查看试题解析
22. 如图14-1，在平面直角坐标系xOy中，直线l₂：y= $- \frac{\sqrt{3}}{3} x + \frac{5 \sqrt{3}}{3}$ 与x轴交于点B，与直线l₁交于点c，c点到x轴的距离CD为2 $\sqrt{3}$ ，直线1交x轴于点A(-3，0) ．

(1)、求直线l₁的函数表达式；

(2)、如图14-2，y轴上的两个动点E、F(E点在F点上方)满足线段EF的长为 $\sqrt{3}$ ，连接CE、AF，当线段CE+EF+AF有最小值时，求出此时点F的坐标，以及CE+EF+AF的最小值；

(3)、如图14-3，将△ACB绕点B逆时针方向旋转60°，得到△BGH，使点A与点H重合，点C与点G重合(C、G两点恰好关于x轴对称)，将ABGH沿直线BC平移，记平移中的△BGH为△B'G'H'，在平移过程中，设直线B'H'与x轴交于点M，是否存在这样的点M，使得△B'MG'为等腰三角形？若存在，请直接写出此时点M的坐标；若不存在，说明理由．

查看试题解析