广东省深圳市罗湖区2021-2022学年第一学期九年级数学期中试卷

试卷更新日期：2021-12-06 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列四个几何体中，它们的主视图、左视图、俯视图都是正方形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列光线所形成的投影不是中心投影的是（）

A、太阳光线 B、台灯的光线 C、手电筒的光线 D、路灯的光线

查看试题解析
3. 掷两枚质地均匀的硬币，两枚硬币全部正面朝上的概率是（）

A、 $1$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
4. 矩形具有而菱形不一定具有的性质是（）

A、两组对边分别平行且相等 B、邻角互补 C、对角线相等 D、对角线互相垂直

查看试题解析
5. 下列命题是真命题的是（）

A、正方形是轴对称图形，但不是中心对称图形 B、对角线互相垂直的平行四边形是矩形 C、四条边相等的四边形是菱形 D、一组对边平行，另一组对边相等的四边形是平行四边形

查看试题解析
6. 如图，在平面直角坐标系中， $△ O A B$ 的顶点坐标为 $O (0 ， 0)$ 、 $A (4 ， 3)$ 和 $B (3 ， 0)$ ．以点O为位似中心，在第三象限内作与 $△ O A B$ 的位似比为 $\frac{1}{3}$ 的位似图形 $△ O C D$ ，则 $△ O C D$ 的面积是（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{3}{2}$ D、 $\frac{9}{2}$

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ A B C = 90 °$ ， $∠ C = 30 °$ ，以点 $A$ 为圆心，以 $A B$ 的长为半径作弧交 $A C$ 于点 $D$ ，连接 $B D$ ，再分别以点 $B ， D$ 为圆心，大于 $\frac{1}{2} B D$ 的长为半径作弧，两弧交于点 $P$ ，作射线 $A P$ 交 $B C$ 于点 $E$ ，连接 $D E$ ，则下列结论中错误的是（）

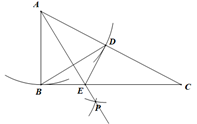A、 $B E = D E$ B、 $D E$ 垂直平分线段 $A C$ C、 $\frac{S_{△ E D C}}{S_{△ A B C}} = \frac{\sqrt{3}}{3}$ D、 $B D^{2} = B C \cdot B E$

查看试题解析
8. 2019年12月以来，湖北省武汉市发现一种新型冠状病毒感染引起的急性呼吸道传染病．感染者的临床表现为：以发热、乏力、干咳为主要表现．在“新冠”初期，有1人感染了“新冠”，经过两轮传染后共有144人感染了“新冠”（这两轮感染因为人们不了解病毒而均未被发现未被隔离），则每轮传染中平均一个人传染了（）

A、10人 B、11人 C、12人 D、13人

查看试题解析
9. 若关于x的方程 $k x^{2} + (k + 2) x + \frac{k}{4} = 0$ 有实数根，则实数k的取值范围是（）

A、 $k \geq - 1$ B、 $k \geq - 1 且 k \neq 0$ C、 $k > - 1 且 k \neq 0$ D、 $k \leq - 1$

查看试题解析
10. 设 $A ， B ， C ， D$ 是反比例函数 $y = \frac{1}{x}$ 图象上的任意四点，现有以下结论：
①存在无数个四边形 $A B C D$ 是平行四边形； ②存在无数个四边形 $A B C D$ 是菱形；

③存在无数个四边形 $A B C D$ 是矩形； ④至少存在一个四边形 $A B C D$ 是正方形.

其中正确结论的个数是（）

A、 $3$ B、 $2$ C、 $1$ D、 $0$

查看试题解析

二、填空题（每题3分，共15分）

11. 已知 $\frac{a}{b} = \frac{1}{3}$ ，则 $\frac{a + b}{b}$ 的值是.

查看试题解析
12. 如图是小孔成像原理的示意图，点 $O$ 与物体 $A B$ 的距离为 $30 c m$ ，与像 $C D$ 的距离是 $14 c m$ ， $A B ∥ C D$ . 若物体 $A B$ 的高度为 $15 c m$ ，则像 $C D$ 的高度是 $c m$ .

查看试题解析
13. 四边形 $A B C D$ ∽四边形 $A^{'} B^{'} C^{'} D^{'}$ ， $∠ A = 70 °$ ， $∠ B^{'} = 108 °$ ， $∠ C^{'} = 92 °$ ，则 $∠ D =$ ．

查看试题解析
14. 如图，矩形 $A B C D$ 的顶点 $D$ 在反比例函数 $y = \frac{k}{x}$ 的图象上，且点 $D$ 在第一象限，顶点 $B ， C$ 在 $x$ 轴上，对角线 $A C$ 的延长线交 $y$ 轴于点 $E$ ，若 $△ B C E$ 的面积是 $12$ ，则 $k =$ .

查看试题解析
15. 如图，在正方形 $A B C D$ 中，以 $A B$ 为腰向正方形内部作等腰 $△ A B E$ （ $A B = A E$ ），点 $G$ 在 $C D$ 上，且 $C G = 3 D G$ ．连接 $B G$ 并延长，与 $A E$ 交于点 $F$ ，与 $A D$ 延长线交于点 $H$ ．连接 $D E$ 交 $B H$ 于点 $K$ ，连接 $C K$ ．若 $A E^{2} = B F \cdot B H$ ， $F G = \frac{13}{10} \sqrt{5}$ ，则 $S_{△ B C K} =$ .

查看试题解析

三、解答题（本大题共55分）

16. 解方程：

(1)、 $x^{2} - 4 x - 5 = 0$

(2)、 $x^{2} + 3 x - 5 = 0$

查看试题解析
17. 如图，在 $△ A B C$ 中，点 $D$ 在 $B C$ 上， $\frac{A D}{A B} = \frac{A E}{A C}$ ， $∠ B A D = ∠ C A E$ ．

(1)、求证： $△ B A C ∽ △ D A E$ ；

(2)、当 $∠ B = 40 °$ 时，求 $∠ A C E$ 的大小．

查看试题解析

18. 在一只不透明的口袋里，装有若干个除了颜色外均相同的小球，某数学学习小组做摸球试验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．如表是活动进行中的一组统计数据：

摸球的次数 $n$	100	150	200	500	800	1000
摸到白球的次数 $m$	59	96	$b$	295	480	601
摸到白球的频率 $\frac{m}{n}$	$a$	0.64	0.58	0.59	0.60	0.601

(1)、请直接写出上表中的

a =

，

b =

；

(2)、请直接写出事件“摸到白球”的概率的估计值是（精确到

0.1

）；

(3)、如果袋中有12个白球，请你估计袋中除了白球外，还有多少个其它颜色的球？

查看试题解析

19. 应用题：（本题第一问要求列方程作答）
某市要组织一次篮球联赛，赛制为单循环形式（每两队之间都赛一场），计划安排15场比赛．

(1)、应该邀请多少支球队参加比赛？

(2)、若某支球队参加3场后，因故不参与以后的比赛，问实际共比赛多少场？

查看试题解析
20. 如图， $O$ 为平行四边形 $A B C D$ 的对称中心，对角线 $A C ⊥ A B$ ，过点 $O$ 作直线 $E F ∥ A B$ ，分别交 $A D ， B C$ 于 $E ， F$ ，连接 $A F ， C E$ ．

(1)、证明：四边形 $A F C E$ 是菱形；

(2)、若四边形 $A F C E$ 是正方形且 $B C = 6$ ，求 $A B$ 的长．

查看试题解析
21. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{k_{2}}{x}$ 的图象相交于 $A 、 B$ 两点，其中点 $A$ 的坐标为 $(- 1 ， 4)$ ，点B的坐标为 $(4 ， n)$ ．

(1)、求这两个函数的表达式；

(2)、根据图象，直接写出满足 $k x + b > \frac{k_{2}}{x}$ 的 $x$ 的取值范围；

(3)、若点 $P$ 在 $y$ 轴上，使得 $S_{△ A B P} = 10$ ，请直接写出点 $P$ 的坐标．

查看试题解析
22. （问题发现）数学小组成员小明做作业时遇到以下问题：

图1 图2 图3

(1)、若四边形 $A B C D$ 是菱形， $∠ A B C = 60 °$ ，点 $P$ 是射线 $B D$ 上一动点，以 $A P$ 为边向右侧作等边 $△ A P E$ ，如图1，当点E在菱形 $A B C D$ 内部或边上时，连接 $C E 、 C A$ ，则 $B P$ 与 $C E$ 有怎样的数量关系？请直接写出你的猜想；

(2)、（类比探究）数学小组对该问题进行进一步探究：
若四边形 $A B C D$ 是正方形，点P是射线 $B D$ 上一动点，以 $A P$ 为直角边在 $A P$ 边的右侧作等腰 $R t △ A P E$ ，其中 $∠ A P E = 90 ° ， A P = P E$ .

①如图2，当点 $P$ 在对角线 $B D$ 上时，小组发现点 $E$ 恰好在射线 $C D$ 上，求 $B P$ 与 $C E$ 之间的数量关系（过程只用说明点 $E$ 在线段 $C D$ 上的情况即可）；

②如图3，当P是对角线 $B D$ 的延长线上一动点时，小组发现点 $E$ 恰好在射线 $C D$ 上，连接 $B E$ ，若 $B E = 6 ， A B = 2$ ，求 $△ B P E$ 的面积．

查看试题解析