2021年初中数学浙教版七年级上册第二章有理数的运算能力阶梯训练——困难版

试卷更新日期：2021-12-06 类型：单元试卷

进入出卷网下载

一、单选题

1. 有理数a在数轴上的位置如图所示，下列各数中，可能在0到1之间的是（）

A、∣a∣-1 B、∣a∣ C、-a D、a+1

查看试题解析
2. 下列说法：①平方等于64的数是8；②若a．b互为相反数，则 $\frac{b}{a} = - 1$ ；③若|-a|=a，则（-a）³的值为负数；④若ab≠0，则 $\frac{a}{| a |} + \frac{b}{| b |}$ 的取值在0，1，2，-2这四个数中，不可取的值是0．正确的个数为（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
3. 2017减去它的 $\frac{1}{2}$ ，再减去余下的 $\frac{1}{3}$ ，再减去余下的 $\frac{1}{4}$ ，…依次类推，一直减到余下的 $\frac{1}{2017}$ ，则最后剩下的数是（）

A、 $0$ B、 $1$ C、 $\frac{2017}{2016}$ D、 $\frac{2016}{2017}$

查看试题解析
4. 我们知道：在整数中，能被2整除的数叫做偶数，反之则为奇数，现把2017个连续整数1，2，3，…，2017的每个数的前面任意填上“+”号或“﹣”号，然后将它们相加，则所得的结果必为（）

A、正数 B、偶数 C、奇数 D、有时为奇数；有时为偶数

查看试题解析
5. 有理数a、b、c在数轴上对应点的位置如图所示，若|b|＞|c|，则下列结论中正确的是（）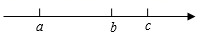

A、abc＜0 B、b＋c＜0 C、a＋c＞0 D、ac＞ab

查看试题解析

二、填空题

6. 某种细菌在培养过程中，每半小时分裂一次（由一个分裂成两个），若这种细菌由1个分裂为16个，则这个过程要经过多长时间？

查看试题解析
7. 两个有理数a、b在数轴上的位置如图所示，则a+b0；ab0（填“＜”或“＞”）．

查看试题解析
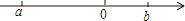8. 有这样一个数字游戏，将1，2，3，4，5，6，7，8，9这九个数字分别填在如图所示的九个空格中，要求每一行从左到右的数字逐渐增大，每一列从上到下的数字也逐渐增大．当数字3和4固定在图中所示的位置时，x代表的数字是，此时按游戏规则填写空格，所有可能出现的结果共有种．

查看试题解析
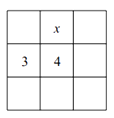9. 若规定“!”是一种数学运算符号，且 $1! = 1, 2! = 2 \times 1 = 2, 3! = 3 \times 2 \times 1 = 6, 4 \times 3 \times 2 \times 1 = 24, \dots$ 则 $\frac{100!}{98!}$ 的值为

查看试题解析
10. 三个有理数a、b、c满足abc>0，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值为．

查看试题解析

三、计算题

11. $- 3^{2} \times {(- \frac{1}{3})}^{2} + (\frac{3}{4} + \frac{1}{6} + \frac{3}{8}) \times (- 24)$

查看试题解析
12. $- {(- 3)}^{2} - [3 + 0.4 \times (- 1 \frac{1}{2})] \div (- 2)$

查看试题解析
13. 列式并计算：

(1)、和是-2，一个加数是6，求另一个加数；

(2)、差是-5，被减数是-7，求减数；

(3)、一个数是16，另一个数比16的相反数小-2，求这两个数的差．

查看试题解析

四、综合题

14. 某出租车驾驶员从公司出发，在南北向的人民路上连续接送5批客人，行驶路程记录如下(规定向南为正，向北为负，单位：km)：

第1批

第2批

第3批

第4批

第5批

5km

2km

-4 km

-3km

10km

(1)、接送完第5批客人后，该驾驶员在公司的什么方向，距离公司多少千米？

(2)、若该出租车每千米耗油0.2升，那么在这个过程中一共耗油多少升？

(3)、若该出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按每千米1.8元收费，在这个过程中该驾驶员共收到车费多少元？

查看试题解析
15. “ $24$ ”点游戏的规则是这样的：在整数范围内任意取四个数，然后进行加、减、乘、除四则运算（每个数只能用一次，可使用小括号、中括号），使其结果等于 $24$ ．例如，取 $2$ ， $3$ ， $6$ ， $9$ 这四个数进行运算，得： $2 \times 6 + 3 + 9 = 24$ ，或 $6 \times 9 \div 2 - 3 = 24$ ，或 $3 \times 9 - 6 \div 2 = 24$ 等．

(1)、用-3，-1，5，3这四个整数，写出 $1$ 种算式，使其运算结果为24；

(2)、用 $- 6$ ， $3$ ， $4$ ， $10$ 这四个整数，写出 $2$ 种不同的算式，使其运算结果为24；

(3)、用 $- 4$ ， $2$ ， $8$ ， $11$ 这四个整数，写出 $1$ 种算式，使其运算结果为 $24$ ．

查看试题解析
16. “分类讨论”是一种重要数学思想方法，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的三个问题.例：三个有理数a，b，c满足 $a b c > 0$ ，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值.
解：由题意得：a，b，c三个有理数都为正数或其中一个为正数，另两个为负数.

①当a，b，c都是正数，即 $a > 0$ ， $b > 0$ ， $c > 0$ 时，

则： $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = \frac{a}{a} + \frac{b}{b} + \frac{c}{c} = 1 + 1 + 1 = 3$ ；

②当a，b，c有一个为正数，另两个为负数时，设 $a > 0$ ， $b < 0$ ， $c < 0$ ，

则： $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = \frac{a}{a} + \frac{- b}{b} + \frac{- c}{c} = 1 + (- 1) + (- 1) = - 1$ ；

综上所述： $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值为3或-1.

请根据上面的解题思路解答下面的问题：

(1)、已知 $| a | = 3$ ， $| b | = 1$ ，且 $a < b$ ，求 $a + b$ 的值；

(2)、已知a，b是有理数，当 $a b \neq 0$ 时，求 $\frac{a}{| a |} + \frac{b}{| b |}$ 的值；

(3)、已知a，b，c是有理数， $a + b + c = 0$ ， $a b c < 0$ .求 $\frac{b + c}{| a |} + \frac{a + c}{| b |} + \frac{a + b}{| c |}$ 的值.

查看试题解析

第1批	第2批	第3批	第4批	第5批
5km	2km	-4 km	-3km	10km

2021年初中数学浙教版七年级上册第二章有理数的运算 能力阶梯训练——困难版

一、单选题

二、填空题

三、计算题

四、综合题

2021年初中数学浙教版七年级上册第二章有理数的运算能力阶梯训练——困难版