2021-2022学年北师版数学八年级上册期末模拟试题一
试卷更新日期:2021-12-04 类型:期末考试
一、单选题
-
1. 下列说法正确的是( )A、了解市民知晓“礼让行人”交通新规的情况,适合全面调查 B、一组数据5,5,3,4,1的中位数是3 C、甲、乙两人9次跳高成绩的方差分别为 甲2 , 乙2 ,说明乙的成绩比甲稳定 D、“经过有交通信号灯的路口,遇到红灯”是随机事件2. 将一副三角板按如图所示的位置摆放在直尺上,则 的度数为( )
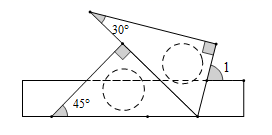 A、70° B、75° C、80° D、85°3. 如图,在Rt△ABC中,∠A=30°,∠C=90°,AB=6,点P是线段AC上一动点,点M在线段AB上,当AM= AB时,PB+PM的最小值为( )
A、70° B、75° C、80° D、85°3. 如图,在Rt△ABC中,∠A=30°,∠C=90°,AB=6,点P是线段AC上一动点,点M在线段AB上,当AM= AB时,PB+PM的最小值为( ) A、3 B、2 C、2 +2 D、3 +34. 下列无理数,与3最接近的是( )A、 B、 C、 D、5. 下列计算正确的是( )A、 3 B、 C、 D、( )2=26. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )
A、3 B、2 C、2 +2 D、3 +34. 下列无理数,与3最接近的是( )A、 B、 C、 D、5. 下列计算正确的是( )A、 3 B、 C、 D、( )2=26. 一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返同,且往返速度的大小不变,两车离甲地的距离 (单位: )与慢车行驶时间 (单位: )的函数关系如图,则两车先后两次相遇的间隔时间是( )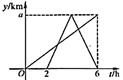 A、 B、 C、 D、7. 已知直线 与 轴、 轴分别交于A、B两点,点P是第一象限内的点,若△PAB为等腰直角三角形,则点P的坐标为( )A、(1,1) B、(1,1)或(1,2) C、(1,1)或(1,2)或(2,1) D、(0,0)或(1,1)或(1,2)或(2,1)8. 九章算术中记载了一个问题,大意是:甲、乙两人各带了若干钱.若甲得到乙所有钱的一半,则甲共有钱50.若乙得到甲所有钱的 ,则乙也共有钱50.甲、乙两人各带了多少钱?设甲带了钱 ,乙带了钱 ,依题意,下面所列方程组正确的是( )A、 B、 C、 D、9. 关于x,y的方程组 的解为 ,若点P(a,b)总在直线y=x上方,那么k的取值范围是( )A、k>1 B、k>﹣1 C、k<1 D、k<﹣110. 如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2交于点A,则方程组的解是( )
A、 B、 C、 D、7. 已知直线 与 轴、 轴分别交于A、B两点,点P是第一象限内的点,若△PAB为等腰直角三角形,则点P的坐标为( )A、(1,1) B、(1,1)或(1,2) C、(1,1)或(1,2)或(2,1) D、(0,0)或(1,1)或(1,2)或(2,1)8. 九章算术中记载了一个问题,大意是:甲、乙两人各带了若干钱.若甲得到乙所有钱的一半,则甲共有钱50.若乙得到甲所有钱的 ,则乙也共有钱50.甲、乙两人各带了多少钱?设甲带了钱 ,乙带了钱 ,依题意,下面所列方程组正确的是( )A、 B、 C、 D、9. 关于x,y的方程组 的解为 ,若点P(a,b)总在直线y=x上方,那么k的取值范围是( )A、k>1 B、k>﹣1 C、k<1 D、k<﹣110. 如图,一次函数y=k1x+b1的图象l1与y=k2x+b2的图象l2交于点A,则方程组的解是( )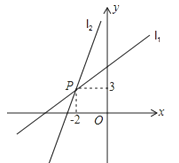 A、 B、 C、 D、11. 一块含有45°的直角三角板和直尺如图放置,若∠1=55°,则∠2的度数是( )
A、 B、 C、 D、11. 一块含有45°的直角三角板和直尺如图放置,若∠1=55°,则∠2的度数是( )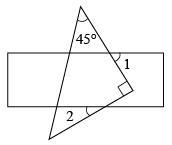 A、30° B、35° C、40° D、45°12. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图像得出如下结论:
A、30° B、35° C、40° D、45°12. 快车从甲地驶往乙地,慢车从乙地驶往甲地,两车同时出发并且在同一条公路上匀速行驶.图中折线表示快、慢两车之间的路程 与它们的行驶时间 之间的函数关系.小欣同学结合图像得出如下结论:①快车途中停留了 ;②快车速度比慢车速度多 ;③图中 ;④快车先到达目的地.其中正确的是( )
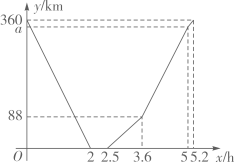 A、①③ B、②③ C、②④ D、①④
A、①③ B、②③ C、②④ D、①④二、填空题
-
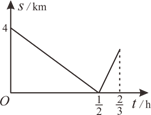
13. 在正比例函数 中,y的值随着x值的增大而增大,则点 在第象限.14. 育红学校七年级学生步行到郊外旅行.七(1)班出发1h后,七(2)班才出发,同时七(2)班派一名联络员骑自行车在两班队伍之间进行联络,联络员和七(1)班的距离s(km)与七(2)班行进时间t(h)的函数关系图象如图所示.若已知联络员用了 第一次返回到自己班级,则七(2)班需要 h才能追上七(1)班.
 15. 人们把 这个数叫做黄金分割数,著名数学家华罗庚优选法中的 法就应用了黄金分割数.设 , ,则 ,记 , ,…, .则 .16. 已知关于x,y的二元一次方程组 满足 ,则a的取值范围是.17. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 、 ,若 , ,则 的度数是.
15. 人们把 这个数叫做黄金分割数,著名数学家华罗庚优选法中的 法就应用了黄金分割数.设 , ,则 ,记 , ,…, .则 .16. 已知关于x,y的二元一次方程组 满足 ,则a的取值范围是.17. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 、 ,若 , ,则 的度数是.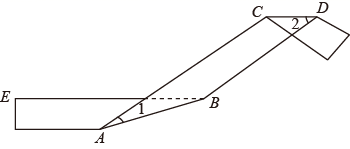 18. 如图,在四边形 中, .设 ,则 (用含 的代数式表示).
18. 如图,在四边形 中, .设 ,则 (用含 的代数式表示).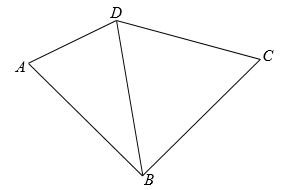
三、解答题
-
19. 计算: .20. 计算:21. 解下列方程组:(1)、(2)、22. 为庆祝中国共产党建党100周年,某校举行了“红色华诞,党旗飘扬”党史知识竞赛.为了解竞赛成绩,抽样调查了七,八年级部分学生的分数,过程如下:
( 1 )收集数据从该校七.八年级学生中各随机抽取20名学生的分数,其中八年级的分数如下:
81 83 84 85 86 87 87 88 89 90
92 92 93 95 95 95 99 99 100 100
( 2 )整理、描述数据按如下分段整理描述样本数据:
分数
人数
年级
七年级
4
6
2
8
八年级
3
4
7
( 3 )分析数据两组样本数据的平均数、中位数、众数、方差如下表所示:
年级
平均数
中位数
众数
方差
七年级
91
89
97
40.9
八年级
91
33.2
根据以上提供的信息,解答下列问题:
①填空: , , ;
②样本数据中,七年级甲同学和八年级乙同学的分数都为90分,同学的分数在本年级抽取的分数中从高到低排序更靠前(填“甲”或“乙”):
③从样本数据分析来看,分数较整齐的是年级(填“七”或“八”);
④如果七年级共有400人参赛,则该年级约有人的分数不低于95分.
23. 本地某快递公司规定:寄件不超过 千克的部分按起步价计费;寄件超过 千克的部分按千克计费.小丽分别寄快递到上海和北京,收费标准及实际收费如下表:收费标准
目的地
起步价(元)
超过 千克的部分
(元 千克)
上海
北京
实际收费
目的地
质量
费用(元)
上海
2
9
北京
3
22
求 , 的值.
24. 小军到某景区游玩,他从景区入口处步行到达小憩屋,休息片刻后继续前行,此时观光车从景区入口处出发的沿相同路线先后到达观景点,如图, , 分别表示小军与观光车所行的路程 与时间 之间的关系.根据图象解决下列问题:
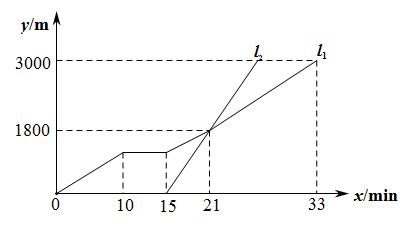 (1)、观光车出发分钟追上小军;(2)、求 所在直线对应的函数表达式;(3)、观光车比小军早几分钟到达观景点?请说明理由.25. 小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1 , y1),P2(x2 , y2),可通过构造直角三角形利用图1得到结论:P1P2= 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x= ,y= .
(1)、观光车出发分钟追上小军;(2)、求 所在直线对应的函数表达式;(3)、观光车比小军早几分钟到达观景点?请说明理由.25. 小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1 , y1),P2(x2 , y2),可通过构造直角三角形利用图1得到结论:P1P2= 他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:x= ,y= . (1)、请你帮小明写出中点坐标公式的证明过程;(2)、①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;
(1)、请你帮小明写出中点坐标公式的证明过程;(2)、①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标:;
(3)、如图3,点P(2,n)在函数y= x(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.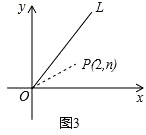 26. 如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
26. 如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.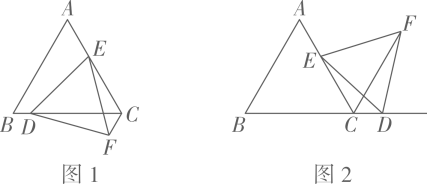 (1)、(问题解决)
(1)、(问题解决)如图1,若点D在边BC上,求证:CE+CF=CD;
(2)、(类比探究)如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.