2021年初中数学浙教版七年级上册第六章图形的基本知识 能力阶梯训练——困难版

试卷更新日期：2021-12-03 类型：单元试卷

进入 出卷网 下载

一、单选题

  • 1. 如图，在线段AB上有C，D两点，CD长度为1cm，AB长为整数，则以A，B，C，D为端点的所有线段长度和不可能为（   ）

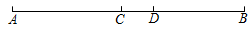    A、16cm B、21cm C、22cm D、31cm

    查看试题解析

  • 2. 如图，点O在直线 AB 上，过O作射线 OC ， ∠BOC=100° ，一直角三角板的直角顶点与点O重合，边 OM 与 OB 重合，边 ON 在直线 AB 的下方．若三角板绕点O按每秒 10° 的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线 ON 恰好平分锐角 ∠AOC ，则t的值为（    ）

    A、5 B、4 C、5或23 D、4或22

    查看试题解析

  • 3. 如图，数轴上点 A ， B ， C 所对应的数分别为 a ， b ， c ，且都不为0，点 C 是线段 AB 的中点，若 |a+b|−|a+b−2c|+|b−2c|−|a−2c|=0 ，则原点 O 的位置（   ）

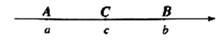    A、在线段 AC 上 B、在线段 CA 的延长线上 C、在线段 BC 上 D、在线段 CB 的延长线上

    查看试题解析

  • 4. 如图，已知A，O，B在一条直线上，∠1是锐角，则∠1的余角是（     ）

    A、12∠2-∠1 B、12∠2-32∠1 C、12∠2-∠1 D、∠2-∠1

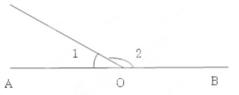    查看试题解析

  • 5. 当式子|x+1|+|x﹣6|取得最小值时，x的取值范围为（   ）
    A、﹣1≤x＜6 B、﹣1≤x≤6 C、x=﹣1或x=6 D、﹣1＜x≤6

    查看试题解析

  • 6. 点A，B，C在同一直线上，已知AB=3cm，BC=1cm，则线段AC的长是（ ）
    A、2cm B、3cm C、4cm D、2cm或4cm

    查看试题解析

  • 7. 两条直线最多有1个交点，三条直线最多有3个交点，四条直线最多有6个交点，那么六条直线最多有 （ ）
    A、21个交点 B、18个交点 C、15个交点 D、10个交点

    查看试题解析

  • 8. 关于长方体有下列三个结论：
    ① 长方体中每一个面都是长方形；② 长方体中每两个面都互相垂直；
    ③ 长方体中相对的两个面是全等的长方形．
    其中结论正确的个数有（   ）

    A、0个； B、1个； C、2个； D、3个.

    查看试题解析

二、作图题

  • 9. 如图

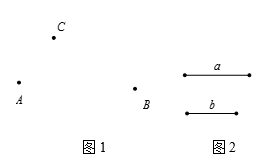    (1)、如图1，平面上有3个点A，B，C．

    ①画直线AB；画射线BC；画线段AC；

    ②过点C作AB的垂线，垂足为点D；

    ③量出点C到直线AB的大约距离．

    (2)、尺规作图：

    已知：线段a，b，如图2．

    求作：一条线段MN，使它等于2a－b．（不写作法，保留作图痕迹）

    查看试题解析

三、综合题

  • 10. 小明同学在数学活动中，将一副三角板按如图1所示的方式放置，其中点B在线段EC上，点D在线段AC上，AB与DE相交于点F，∠C＝90°，∠A＝30°，∠E＝45°．

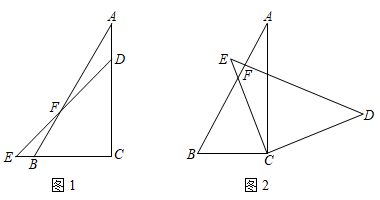    (1)、求∠BFD的度数；
    (2)、如图2，当小明将三角板DCE绕点C转动到ED⊥AB时，求∠BCE的度数；
    (3)、小明思考：在转动三角板DCE的过程中，当0°＜∠BCE＜180°，且点E在直线BC的上方时，是否存在DE与三角板ABC的一条边互相平行？若存在，请你帮小明直接写出∠BCE所有可能的值；若不存在，请说明理由

    查看试题解析

  • 11. 已知∠AOB＝110°，∠COD＝40°，OE平分∠AOC，OF平分∠BOD.

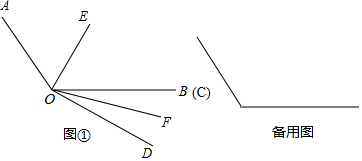    (1)、如图①，当OB、OC重合时，求∠AOE﹣∠BOF的值；
    (2)、当∠COD从图①所示位置绕点O以每秒3°的速度顺时针旋转t秒（0＜t＜10）；在旋转过程中∠AOE﹣∠BOF的值是否会因t的变化而变化，若不发生变化，请求出该定值；若发生变化，请说明理由.

    查看试题解析