广西壮族自治区贵港市覃塘区2021-2022学年八年级上学期数学期中考试试卷

试卷更新日期：2021-12-03 类型：期中考试

进入出卷网下载

一、单选题

1. 下列代数式中，不属于分式的是（）

A、 $\frac{1}{π}$ B、 $\frac{1}{x}$ C、 $\frac{a b}{a}$ D、 $- \frac{3}{1 - x}$

查看试题解析
2. 如果分式 $\frac{| m | - 4}{| m - 4 |}$ 的值等于0，那么m的值为（）

A、±4 B、4 C、﹣4 D、不存在

查看试题解析
3. 下列各组中的三条线段恰好是一个三角形三条边的是（）

A、3，4，7 B、3，4，10 C、3，7，10 D、4，7，10

查看试题解析
4. 分式方程 $\frac{2}{x - 1} = \frac{1}{x}$ 的解是（）

A、x＝0 B、x＝1 C、x＝﹣1 D、x＝﹣2

查看试题解析
5. △ABC中，若∠A＋∠B＝∠C，则△ABC是(　　)

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
6. 下列计算正确的是（）

A、（ $\frac{b}{a}$ ）³ $= \frac{b^{3}}{a}$ B、 $\frac{- a - b}{a - b} = - 1$ C、 $\frac{1}{a} + \frac{2}{b} = \frac{3}{a + b}$ D、a² $\div \frac{1}{a} =$ a³

查看试题解析
7. 若一个等腰三角形的顶角为120°，则它的外角的度数为（）

A、60°或30° B、150°或60° C、30° D、150°

查看试题解析
8. 对于下列命题：①若a²＞b² ，则|a|＞|b|；②若a+b＝0，则|a|＝|b|；③等边三角形的三个内角都相等；其中原命题与逆命题均为真命题的是（）

A、①②③ B、①② C、①③ D、②③

查看试题解析
9. 若关于x的分式方程 $\frac{k x}{x^{2} - 4} = \frac{3}{x + 2} - \frac{2}{x - 2}$ 无解，则k的值为（）

A、1或﹣4或6 B、1或4或﹣6 C、﹣4或6 D、4或﹣6

查看试题解析
10. 如图，一张含有80°的三角形纸片，剪去这个80°角后，得到一个四边形，则∠1+∠2的度数是（）

A、200° B、240° C、260° D、300°

查看试题解析
11. 如图，在 $△$ ABC中，边BC的垂直平分线分别交AC，BC于点D，E，若 $△$ ABC的周长为12，CE $= \frac{5}{2}$ ，则 $△$ ABD的周长为（）

A、10 B、9 C、8 D、7

查看试题解析
12. 如图，AB＝CD，且AB⊥CD，作CE⊥AD，BF⊥AD，垂足分别是E，F，若CE＝m，BF＝n，EF＝k，则线段AD的长是（）

A、m﹣n＝k B、m+n﹣k C、m+k D、n+k

查看试题解析

二、填空题

13. 若分式 $\frac{x - 1}{x + 2}$ 的值不存在，则x的值是.

查看试题解析
14. 计算：2⁰•2^﹣3＝.

查看试题解析
15. 世界上最小的开花结果的植物的果实像一个微小的无花果，其质量只有7.6×10^﹣8g.将7.6×10^﹣8用小数表示为 .

查看试题解析
16. 如图，已知 $a ∥ b$ ，∠2＝95°，∠3＝140°，则∠1的度数为.

查看试题解析
17. 如图，已知ABC是等腰直角三角形，∠ACB＝90°，AD⊥DE于点D，BE⊥DE于点E，且点C在DE上，若AD＝5，BE＝8，则DE的长为.

查看试题解析
18. 如图，已知AB＝AC，∠ABD＝∠ACF，∠ADB＝∠AFC，点D、E、F、C在同一条直线上，对于下列四个结论：① $△$ ABD≌ $△$ ACF；②AD＝AF；③∠DAF＝∠BAC；④ $△$ BCE≌ $△$ BAD.其中正确结论的序号是.

查看试题解析

三、解答题

19. 计算：

(1)、（ $\frac{a^{- 2}}{b^{3}}$ ）²÷（ $\frac{a^{- 2}}{b^{3}}$ ）³•（ $\frac{a^{- 2}}{b^{3}}$ ）^﹣⁴；

(2)、 $\frac{a - 2}{1 + 2 a + a^{2}} \div$ （a $- \frac{3 a}{a + 1}$ ）.

查看试题解析
20. 尺规作图（只保留作图痕迹，不要求写出作法）：如图，已知线段m和∠α，求作：Rt $△$ ABC，使斜边AB＝m，∠A＝∠α.

查看试题解析
21. 解下列分式方程：

(1)、 $\frac{2 x}{x + 3} = \frac{1}{x + 3} + 1$ ；

(2)、 $\frac{x}{x - 1} + \frac{4}{1 - x^{2}} = 1$ .

查看试题解析
22. 如图，在等边 $△$ ABC中，点D在BC边上，点E在△ABC外，AD＝AE.若∠BAD＝20°，∠DAE＝70°，求∠CAE和∠CDE的度数.

查看试题解析
23. 先化简，再求值：

(1)、 $\frac{m}{m^{2} - m} \cdot \frac{m^{2} - 1}{m + 1} - \frac{m}{m - 1}$ ，其中m＝2.

(2)、（1 $- \frac{1}{x - 1}$ ） $\div \frac{x^{2} - 4 x + 4}{x^{2} - x}$ ，其中x＝﹣3.

查看试题解析
24. 如图，点A，B，C在同一直线上，点E在BD上，且 $△$ ABD≌ $△$ EBC.

(1)、若AB＝2，BC＝3，求DE的长；

(2)、判断AD与CE所在直线的位置关系，并说明理由.

查看试题解析
25. 某商店以固定进价一次性购进一种商品，3月份按一定售价销售，销售额为2400元，为扩大销量，减少库存，4月份在3月份售价基础上打9折销售，结果销售量增加30件，销售额增加840元．

(1)、求该商店3月份这种商品的售价是多少元？

(2)、如果该商店3月份销售这种商品的利润为900元，那么该商店4月份销售这种商品的利润是多少元？

查看试题解析
26. 如图，已知 $△$ ABC是等边三角形，点M，N分别在CB，BC的延长线上，且BM＝CN.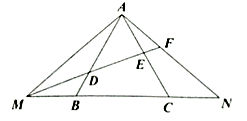

(1)、求证：AM＝AN；

(2)、在（1）的条件下，作∠AMN的平分线MF，MF与AB，AC，AN分别交于点D，E，F，若AD＝MD.求证：MF＝AC+CN.

查看试题解析