广西壮族自治区防城港市上思县2021-2022学年八年级上学期数学期中考试试卷
试卷更新日期：2021-12-03 类型：期中考试
一、单选题
-
1. 以下列各组线段为边，能组成三角形的是（ ）.A、2cm，3cm，5cm B、5cm，6cm，10cm C、1cm，1cm，3cm D、3cm，4cm，9cm2. 下列说法错误的是（ ）.A、锐角三角形的三条高线，三条中线，三条角平分线分别交于一点 B、钝角三角形有两条高线在三角形外部 C、直角三角形只有一条高线 D、任意三角形都有三条高线，三条中线，三条角平分线3. 下列图形中具有稳定性的是（ ）A、正方形 B、钝角三角形 C、长方形 D、四边形4. 九边形的对角线有（ ）A、25条 B、31条 C、27条 D、30条5. 如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A=60°，∠B=40°，则∠ECD等于（ ）
A、40° B、45° C、50° D、55°6. 一个正多边形的内角和是540°，则该正多边形的一个外角的度数为（ ）A、45° B、55° C、60° D、72°7. 下列说法错误的是（ ）A、全等三角形的对应高相等 B、全等三角形的对应中线相等 C、全等三角形对应的角平分线相等 D、所有的等边三角形都全等8. 如图所示，若AB DE，且∠E=55°，则∠B+∠C的度数是（ ）
A、135° B、125° C、55° D、45°9. 如图，AB＝AD，CB＝CD，∠B＝30°，∠BAD＝46°，则∠ACD的度数是（ ）
A、120° B、125° C、127° D、104°10. 有下列四种说法：①角的内部任意一点到角的两边的距离相等；②到角的两边距离相等的点在这个角的平分线上；③角的平分线上任意一点到角的两边的距离相等；④在 ABC中的∠BAC的平分线上任意一点到三角形三边的距离相等，其中正确的有（ ）A、1 B、2 C、3 D、411. 如图，把三角形ABC沿着DE折叠后，点A落在四边形BCED的内部 ，若∠A=45°，则∠1+∠2等于（ ）
A、60° B、90° C、120° D、135°12. 如图，某人从点A出发，前进8m后向右转60°，再前进8m后又向右转60°，按照这样的方式一直走下去，当他第一次回到出发点A时，共走了（ ）
A、24m B、32m C、40m D、48m二、填空题
-
13. 若三角形的两条边的长分别为4和5，第三边的长为x，则x 的取值范围是.14. 如图所示，∠BAC的外角∠CAE等于100°，∠B=45°，则∠C的度数是.
15. 若等腰三角形的两边长分别为3cm和8cm，则它的周长是.16. 如图，由于受第18号台风“圆规”的影响，学校的某玻璃三角板摔成三块，派小明同学到玻璃店再配一块同样大小的三角板，让小明最省事的方法是带去.
17. 将三角尺按右图所示的方式放置在一张长方形纸片上， ， ， ，则 的度数为.
18. 如图，在梯形ABCD中， ，点M是AD 的中点，且MB=MC.若AD=4，AB=6，BC=8，则梯形ABCD的周长是.
三、解答题
-
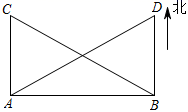
19. 如图，AC，BD相交于点O，且AB=DC，AC=DB，求证：∠A=∠D.
20. 如图，点A、D、C、F在同一条直线上，AD=CF，AB=DE，BC=EF.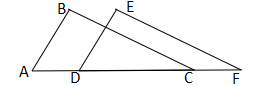
(1)、求证：ΔABC≌△DEF；(2)、若∠A=55°，∠B=88°，求∠F的度数.21. 尺规作图（只保留作图痕迹，不要求写出作法）：如图，已知 ，请根据“ ”基本事实作出 ，使 .
22. 如图，已知∠C＝∠D＝90°，BC与AD交于点E，AC＝BD，求证：AE＝BE.
23. 如图，AB=AD，BC=DC，点E在AC上.
(1)、求证：AC平分∠BAD；(2)、求证：BE=DE.
