辽宁省沈阳市五校协作体2021-2022学年高一上学期数学期中联考试卷
试卷更新日期:2021-12-03 类型:期中考试
一、单选题
-
1. 设集合 ,则满足条件 的集合N的个数是( )A、3 B、4 C、7 D、82. 已知a,b是实数,则“|a+b|=|a|+|b|”是“ab>0”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件3. 函数 的图象大致为( )A、
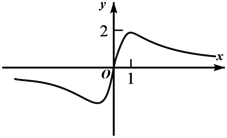 B、
B、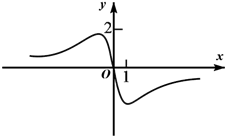 C、
C、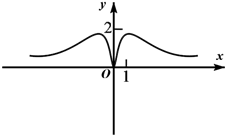 D、
D、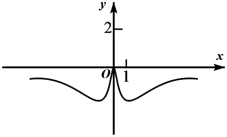 4. 关于x的方程 的根为 , ,则代数式 的值为( )A、2 B、-4 C、4 D、-25. 函数 的定义域为 ,则函数 的定义域为( )A、 B、 C、 D、6. 若不等式 在区间 上有解,则实数a的取值范围是( )A、 B、 C、 D、7. 函数 的值域为( )A、 B、 C、 D、8. 是定义在R上的奇函数,当 时, ,若 对一切 成立,则实数a的取值范围是( )A、 B、 C、 D、
4. 关于x的方程 的根为 , ,则代数式 的值为( )A、2 B、-4 C、4 D、-25. 函数 的定义域为 ,则函数 的定义域为( )A、 B、 C、 D、6. 若不等式 在区间 上有解,则实数a的取值范围是( )A、 B、 C、 D、7. 函数 的值域为( )A、 B、 C、 D、8. 是定义在R上的奇函数,当 时, ,若 对一切 成立,则实数a的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 设函数 , 的定义域为R , 且 是奇函数, 是偶函数,则下列说法中正确的是( )A、 是偶函数 B、 是偶函数 C、 是奇函数 D、 是奇函数10. 使得函数 在区间 上单调递增的实数a可能的取值是( )A、2 B、1 C、0 D、-111. 下列命题中说法正确的是( )A、若 ,则 的最小值为2 B、若 , ,则 的最小值为3 C、若a , ,且 ,则 的最小值为 D、若 ,则 的最小值为412. 已知函数 ,若关于x的方程 有且仅有9个不同的根,则实数a可能的取值是( )A、 B、 C、 D、1
三、填空题
-
13. 当 时,则函数 的值域为 .14. 若函数 在R上为增函数,则实数a的取值范围是 .15. 函数 ,则关于x的不等式 的解集是 .16. 已知函数 满足 ,又函数 ,若 ,则 的值为 .
四、解答题
-
17. 已知集合 ,非空集合 .(1)、当 时,求 ;(2)、求使得 成立的实数a的取值范围.18. 已知命题p:“ ,函数 无零点”,命题q:“方程 有两个不相等的正实数根”,若命题p与命题q有且只有一个真命题,求实数m的取值范围.19. 已知函数 .(1)、方程 的一根在区间 内,另一根在区间 内,求实数m的取值范围;(2)、方程 的两个不等根都在区间 上,求实数m的取值范围.