2021-2022学年北师版数学九年级下册《第三章 圆》单元检测B卷
试卷更新日期:2021-12-02 类型:单元试卷
一、单选题
-
1. 已知平面内有⊙O和点A , B , 若⊙O半径为2cm , 线段OA=3cm , OB=2cm , 则直线AB与⊙O的位置关系为( )A、相离 B、相交 C、相切 D、相交或相切2. 往水平放置的半径为 的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度 ,则水的最大深度为( )
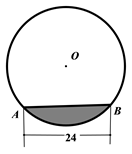 A、 B、 C、 D、3. 如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于( )
A、 B、 C、 D、3. 如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于( ) A、 B、 C、 D、4. 如图,△BCD内接于⊙O,∠D=70°,OA⊥BC交⨀O于点A,连接AC,则∠OAC的度数为( )
A、 B、 C、 D、4. 如图,△BCD内接于⊙O,∠D=70°,OA⊥BC交⨀O于点A,连接AC,则∠OAC的度数为( ) A、40° B、55° C、70° D、110°5. 如图,点C是以点O为圆心,AB为直径的半圆上一点,连接AC,BC,OC.若AC=4,BC=3,则sin∠BOC的值是( )
A、40° B、55° C、70° D、110°5. 如图,点C是以点O为圆心,AB为直径的半圆上一点,连接AC,BC,OC.若AC=4,BC=3,则sin∠BOC的值是( )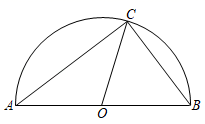 A、1 B、 C、 D、6. 如图,A , B , C是⊙O上的三点,若 ,则 的度数是( )
A、1 B、 C、 D、6. 如图,A , B , C是⊙O上的三点,若 ,则 的度数是( ) A、40° B、35° C、30° D、25°7. 如图,AB为 的直径,C , D为 上的两点,若 ,则 的度数为( )
A、40° B、35° C、30° D、25°7. 如图,AB为 的直径,C , D为 上的两点,若 ,则 的度数为( )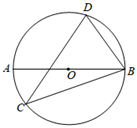 A、 B、 C、 D、8. 如图, 与正五边形 的两边 相切于 两点,则 的度数是( )
A、 B、 C、 D、8. 如图, 与正五边形 的两边 相切于 两点,则 的度数是( )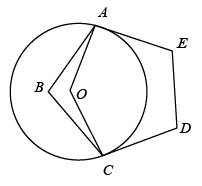 A、 B、 C、 D、9. 如图,∠BAC=36°,点O在边AB上,⊙O与边AC相切于点D,交边AB于点E,F,连接FD,则∠AFD等于( )
A、 B、 C、 D、9. 如图,∠BAC=36°,点O在边AB上,⊙O与边AC相切于点D,交边AB于点E,F,连接FD,则∠AFD等于( )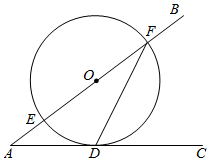 A、27° B、29° C、35° D、37°10. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )
A、27° B、29° C、35° D、37°10. 如图, 是 的弦,点 在过点 的切线上, , 交 于点 .若 ,则 的度数等于( )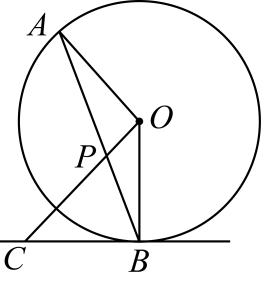 A、 B、 C、 D、11. 如图,ABCDEF为⊙O的内接正六边形,AB=a,则图中阴影部分的面积是( )
A、 B、 C、 D、11. 如图,ABCDEF为⊙O的内接正六边形,AB=a,则图中阴影部分的面积是( ) A、 B、( )a2 C、 2 D、( )a212. 如图,弧长为半圆的弓形在坐标系中,圆心在 .将弓形沿x轴正方向无滑动滚动,当圆心经过的路径长为 时,圆心的横坐标是( )
A、 B、( )a2 C、 2 D、( )a212. 如图,弧长为半圆的弓形在坐标系中,圆心在 .将弓形沿x轴正方向无滑动滚动,当圆心经过的路径长为 时,圆心的横坐标是( )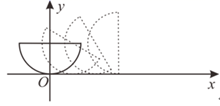 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图, 是 的直径,点 在 上,若 ,则 °.
 14. 如图, 内接于 , ,点 是 的中点,连接 , , ,则 .
14. 如图, 内接于 , ,点 是 的中点,连接 , , ,则 .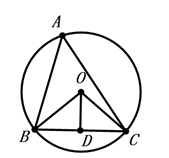 15. 如图,在圆内接五边形ABCDE中,∠EAB∠+∠C+∠CDE+∠E=430°,则∠CDA=度.
15. 如图,在圆内接五边形ABCDE中,∠EAB∠+∠C+∠CDE+∠E=430°,则∠CDA=度. 16. 如图,在平面直角坐标系 中,点A在 轴负半轴上,点B在 轴正半轴上,⊙D经过A , B , O , C四点,∠ACO=120°,AB=4,则圆心点D的坐标是
16. 如图,在平面直角坐标系 中,点A在 轴负半轴上,点B在 轴正半轴上,⊙D经过A , B , O , C四点,∠ACO=120°,AB=4,则圆心点D的坐标是 17. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是cm2
17. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(即阴影部分)面积之和是cm2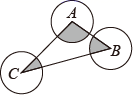 18. 如图,在 的正方形网格图中,已知点A、B、C、D、O均在格点上,其中A、B、D又在 上,点E是线段 与 的交点.则 的正切值为.
18. 如图,在 的正方形网格图中,已知点A、B、C、D、O均在格点上,其中A、B、D又在 上,点E是线段 与 的交点.则 的正切值为.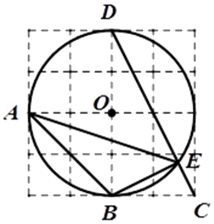
三、解答题
-
19. 如图, 是 的外接圆,点E是 的内心,AE的延长线交BC于点F,交 于点D,连接BD,BE.
 (1)、求证: ;(2)、若 , ,求DB的长.20. 如图,在 中, ,点E在BC边上,过A,C,E三点的 交AB边于另一点F,且F是弧AE的中点,AD是 的一条直径,连接DE并延长交AB边于M点.
(1)、求证: ;(2)、若 , ,求DB的长.20. 如图,在 中, ,点E在BC边上,过A,C,E三点的 交AB边于另一点F,且F是弧AE的中点,AD是 的一条直径,连接DE并延长交AB边于M点.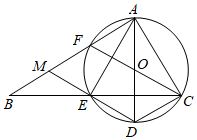 (1)、求证:四边形CDMF为平行四边形;(2)、当 时,求 的值.21. 如图,直线 经过 上的点 ,直线 与 交于点 和点 , 与 交于点 ,与 交于点 , , .
(1)、求证:四边形CDMF为平行四边形;(2)、当 时,求 的值.21. 如图,直线 经过 上的点 ,直线 与 交于点 和点 , 与 交于点 ,与 交于点 , , . (1)、求证: 是 的切线;(2)、若 , ,求图中阴影部分面积.22. 如图,在⊙ 中, 是直径, ,垂足为P,过点 的 的切线与 的延长线交于点 , 连接 .
(1)、求证: 是 的切线;(2)、若 , ,求图中阴影部分面积.22. 如图,在⊙ 中, 是直径, ,垂足为P,过点 的 的切线与 的延长线交于点 , 连接 .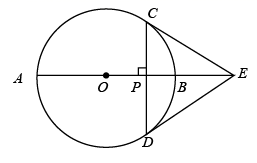 (1)、求证: 为⊙ 的切线;(2)、若⊙ 半径为3, ,求 .23. 如图,⊙O是 ABC的外接圆,AD是⊙O的直径,F是AD延长线上一点,连接CD,CF,且∠DCF=∠CAD.
(1)、求证: 为⊙ 的切线;(2)、若⊙ 半径为3, ,求 .23. 如图,⊙O是 ABC的外接圆,AD是⊙O的直径,F是AD延长线上一点,连接CD,CF,且∠DCF=∠CAD.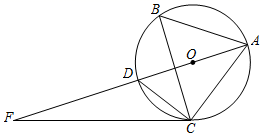 (1)、求证:CF是⊙O的切线;(2)、若cosB= ,AD=2,求FD的长.
(1)、求证:CF是⊙O的切线;(2)、若cosB= ,AD=2,求FD的长.

