2021-2022学年北师版数学九年级下册《第二章 二次函数》单元检测B卷
试卷更新日期:2021-12-02 类型:单元试卷
一、单选题
-
1. 若抛物线 与x轴两个交点间的距离为4.对称轴为 ,P为这条抛物线的顶点,则点P关于x轴的对称点的坐标是( )A、 B、 C、 D、2. 已知A、B两点的坐标分别为(3,﹣4)、(0,﹣2),线段AB上有一动点M(m,n),过点M作x轴的平行线交抛物线y=a(x﹣1)2+2于P(x1 , y1)、Q(x2 , y2)两点.若x1<m≤x2 , 则a的取值范围为( )A、﹣4≤a<﹣ B、﹣4≤a≤﹣ C、﹣ ≤a<0 D、﹣ <a<03. 已知抛物线 上的部分点的横坐标x与纵坐标y的对应值如表:
x
…
-1
0
1
2
3
…
y
…
3
0
-1
m
3
…
以下结论正确的是( )
A、抛物线 的开口向下 B、当 时,y随x增大而增大 C、方程 的根为0和2 D、当 时,x的取值范围是4. 二次函数 ( 、 、 是常数,且 )的自变量 与函数值 的部分对应值如下表:…
0
1
2
…
…
2
2
…
且当 时,对应的函数值 .有以下结论:① ;② ;③关于 的方程 的负实数根在 和0之间;④ 和 在该二次函数的图象上,则当实数 时, .其中正确的结论是( )
A、①② B、②③ C、③④ D、②③④5. 若二次函数 的图象如图所示,则一次函数 与反比例函数 在同一个坐标系内的大致图象为( )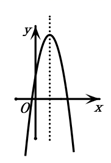 A、
A、 B、
B、 C、
C、 D、
D、 6. 将抛物线y=(x﹣1)2+2向左平移3个单位长度,再向下平移4个单位长度所得到的抛物线的解析式为( )A、y=x2﹣8x+22 B、y=x2﹣8x+14 C、y=x2+4x+10 D、y=x2+4x+27. 如图,二次函数 的图象经过点 , ,与y轴交于点C . 下列结论:
6. 将抛物线y=(x﹣1)2+2向左平移3个单位长度,再向下平移4个单位长度所得到的抛物线的解析式为( )A、y=x2﹣8x+22 B、y=x2﹣8x+14 C、y=x2+4x+10 D、y=x2+4x+27. 如图,二次函数 的图象经过点 , ,与y轴交于点C . 下列结论:① ;②当 时,y随x的增大而增大;③ ;④ .
其中正确的个数有( )
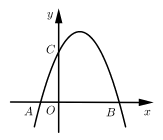 A、1个 B、2个 C、3个 D、4个8. 如图,抛物线y=ax2+bx+c(a≠0)的顶点为(1,n),与x轴的一个交点B(3,0),与y轴的交点在(0,﹣3)和(0,﹣2)之间.下列结论中:① 0;②﹣2<b ;③(a+c)2﹣b2=0;④2c﹣a<2n , 则正确的个数为( )
A、1个 B、2个 C、3个 D、4个8. 如图,抛物线y=ax2+bx+c(a≠0)的顶点为(1,n),与x轴的一个交点B(3,0),与y轴的交点在(0,﹣3)和(0,﹣2)之间.下列结论中:① 0;②﹣2<b ;③(a+c)2﹣b2=0;④2c﹣a<2n , 则正确的个数为( ) A、1 B、2 C、3 D、49. 抛物线 经过点 、 ,且与y轴交于点 ,则当 时,y的值为( )A、-5 B、-3 C、-1 D、510. 如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是( )
A、1 B、2 C、3 D、49. 抛物线 经过点 、 ,且与y轴交于点 ,则当 时,y的值为( )A、-5 B、-3 C、-1 D、510. 如图是王阿姨晚饭后步行的路程s(单位:m)与时间t(单位:min)的函数图象,其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是( ) A、25min~50min,王阿姨步行的路程为800m B、线段CD的函数解析式为 C、5min~20min,王阿姨步行速度由慢到快 D、曲线段AB的函数解析式为11. 三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A、25min~50min,王阿姨步行的路程为800m B、线段CD的函数解析式为 C、5min~20min,王阿姨步行速度由慢到快 D、曲线段AB的函数解析式为11. 三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( ) A、4 米 B、5 米 C、2 米 D、7米12. 如图,二次函数 图象的一部分与x轴的一个交点坐标为 ,对称轴为 ,结合图象给出下列结论:
A、4 米 B、5 米 C、2 米 D、7米12. 如图,二次函数 图象的一部分与x轴的一个交点坐标为 ,对称轴为 ,结合图象给出下列结论:
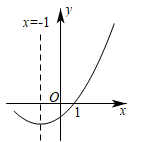
① ;
② ;
③关于x的一元二次方程 的两根分别为-3和1;
④若点 , , 均在二次函数图象上,则 ;
⑤ (m为任意实数).
其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
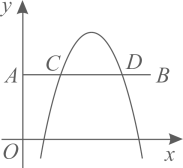
13. 从 中任取一数作为 ,使抛物线 的开口向上的概率为 .14. 平面直角坐标系 中,已知点 ,且实数m,n满足 ,则点P到原点O的距离的最小值为.15. 抛物线 与x轴有交点,则k的取值范围是.16. 某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为元.17. 如图,在平面直角坐标系中,点A的坐标为 ,点B的坐标为 .若抛物线 (h、k为常数)与线段 交于C、D两点,且 ,则k的值为 .
 18. 如图,二次函数 的图象与x轴的正半轴交于点A , 对称轴为直线 ,下面结论:
18. 如图,二次函数 的图象与x轴的正半轴交于点A , 对称轴为直线 ,下面结论: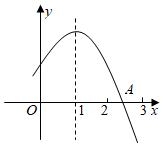
① ;
② ;
③ ;
④方程 必有一个根大于 且小于0.
其中正确的是(只填序号).
三、解答题
-
19. 某药店选购了一批消毒液,进价为每瓶10元,在销售过程中发现销售量y(瓶)与每瓶售价x(元)之间存在一次函数关系(其中 ,且x为整数),当每瓶消毒液售价为12元时,每天销售量为90瓶;当每瓶消毒液售价为15元时,每天销售量为75瓶;(1)、求y与x之间的函数关系式;(2)、设该药店销售该消毒液每天的销售利润为w元,当每瓶消毒液售价为多少元时,药店销售该消毒液每天销售利润最大.20. 如图,抛物线 与 轴相交于A,B两点,与y轴相交于点C,对称轴为直线 ,顶点为D,点B的坐标为 .
 (1)、填空:点A的坐标为 , 点D的坐标为 , 抛物线的解析式为;(2)、当二次函数 的自变量:满足 时,函数y的最小值为 ,求m的值;(3)、P是抛物线对称轴上一动点,是否存在点P,使 是以AC为斜边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.21. 如图,已知抛物线y=a(x﹣3)(x+6)过点A(﹣1,5)和点B(﹣5,m)与x轴的正半轴交于点C.
(1)、填空:点A的坐标为 , 点D的坐标为 , 抛物线的解析式为;(2)、当二次函数 的自变量:满足 时,函数y的最小值为 ,求m的值;(3)、P是抛物线对称轴上一动点,是否存在点P,使 是以AC为斜边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.21. 如图,已知抛物线y=a(x﹣3)(x+6)过点A(﹣1,5)和点B(﹣5,m)与x轴的正半轴交于点C.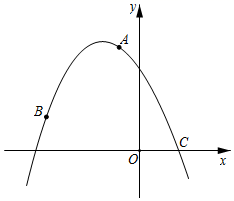 (1)、求a,m的值和点C的坐标;(2)、若点P是x轴上的点,连接PB,PA,当 时,求点P的坐标;(3)、在抛物线上是否存在点M,使A,B两点到直线MC的距离相等?若存在,求出满足条件的点M的横坐标;若不存在,请说明理由.22. 如图,已知抛物线y=ax2+bx+c与x轴相交于A(-3,0),B两点,与y轴相交于点C(0,2),对称轴是直线x=-1,连接AC.
(1)、求a,m的值和点C的坐标;(2)、若点P是x轴上的点,连接PB,PA,当 时,求点P的坐标;(3)、在抛物线上是否存在点M,使A,B两点到直线MC的距离相等?若存在,求出满足条件的点M的横坐标;若不存在,请说明理由.22. 如图,已知抛物线y=ax2+bx+c与x轴相交于A(-3,0),B两点,与y轴相交于点C(0,2),对称轴是直线x=-1,连接AC.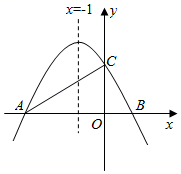 (1)、求该抛物线的表达式;(2)、若过点B的直线l与抛物线相交于另一点D,当∠ABD=∠BAC时,求直线l的表达式;(3)、在(2)的条件下,当点D在x轴下方时,连接AD,此时在y轴左侧的抛物线上存在点P,使 ,请直接写出所有符合条件的点P的坐标.23. 如图1,二次函数 的图象交坐标轴于点 , ,点 为 轴上一动点.
(1)、求该抛物线的表达式;(2)、若过点B的直线l与抛物线相交于另一点D,当∠ABD=∠BAC时,求直线l的表达式;(3)、在(2)的条件下,当点D在x轴下方时,连接AD,此时在y轴左侧的抛物线上存在点P,使 ,请直接写出所有符合条件的点P的坐标.23. 如图1,二次函数 的图象交坐标轴于点 , ,点 为 轴上一动点. (1)、求二次函数 的表达式;(2)、过点 作 轴分别交线段 ,抛物线于点 , ,连接 .当 时,求 的面积;(3)、如图2,将线段 绕点 逆时针旋转90得到线段 .
(1)、求二次函数 的表达式;(2)、过点 作 轴分别交线段 ,抛物线于点 , ,连接 .当 时,求 的面积;(3)、如图2,将线段 绕点 逆时针旋转90得到线段 .①当点 在抛物线上时,求点 的坐标;
②点 在抛物线上,连接 ,当 平分 时,直接写出点P的坐标.
24. 如图,抛物线 与 轴交于 、 两点,与 轴交于点 .直线 与抛物线交于 、 两点,与 轴交于点 ,点 的坐标为 .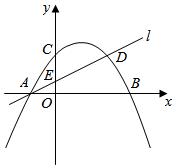 (1)、求抛物线的解析式与直线 的解析式;(2)、若点 是抛物线上的点且在直线 上方,连接 、 ,求当 面积最大时点 的坐标及该面积的最大值;(3)、若点 是 轴上的点,且 ,求点 的坐标.25. 在平面直角坐标系中,O为原点, 是等腰直角三角形, ,顶点 ,点B在第一象限,矩形 的顶点 ,点C在y轴的正半轴上,点D在第二象限,射线 经过点B.
(1)、求抛物线的解析式与直线 的解析式;(2)、若点 是抛物线上的点且在直线 上方,连接 、 ,求当 面积最大时点 的坐标及该面积的最大值;(3)、若点 是 轴上的点,且 ,求点 的坐标.25. 在平面直角坐标系中,O为原点, 是等腰直角三角形, ,顶点 ,点B在第一象限,矩形 的顶点 ,点C在y轴的正半轴上,点D在第二象限,射线 经过点B.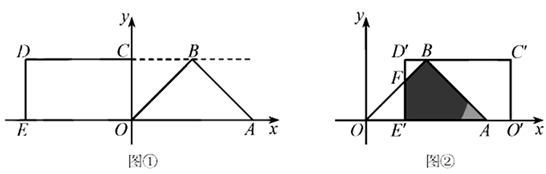
(Ⅰ)如图①,求点B的坐标;
(Ⅱ)将矩形 沿x轴向右平移,得到矩形 ,点O,C,D,E的对应点分别为 , , , ,设 ,矩形 与 重叠部分的面积为S.
①如图②,当点 在x轴正半轴上,且矩形 与 重叠部分为四边形时, 与 相交于点F,试用含有t的式子表示S,并直接写出t的取值范围;
②当 时,求S的取值范围(直接写出结果即可).