贵州省玉屏侗族自治县2021-2022学年八年级上学期期中考试数学试题

试卷更新日期：2021-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. 要使分式 $\frac{2 x - 3}{x - 2}$ 有意义， $x$ 的取值范围是（）

A、 $x \neq 2$ B、 $x \neq 0$ C、 $x \neq - 2$ D、 $x \neq \frac{3}{2}$

查看试题解析
2. 等腰三角形的一个外角为80°，则它的底角为（　　）

A、100° B、80° C、40° D、100°或40°

查看试题解析
3. 如图，在 $△ A B C$ 中， $∠ A = 30 °$ ， $∠ B = 50 °$ ， $C D$ 平分 $∠ A C B$ ，则 $∠ A D C$ 的度数是（）

A、 $80 °$ B、 $90 °$ C、 $100 °$ D、 $110 °$

查看试题解析
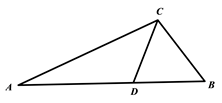4. 若等腰三角形中有两边长分别为2和5，则这个三角形的周长为（　　）

A、9 B、12 C、7或9 D、9或12

查看试题解析
5.
如图，若△ABC≌△DEF，∠A=45°，∠F=35°，则∠E等于（　　）

A、35° B、45° C、60° D、100°

查看试题解析
6. 有下列命题：①两点之间，线段最短； ②相等的角是对顶角； ③当a＞0时，|a|＝a； ④内错角互补，两直线平行．其中真命题的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 若 $a \neq b$ ，则下列分式化简正确的是（）

A、 $\frac{a + 2}{b + 2} = \frac{a}{b}$ B、 $\frac{a - 2}{b - 2} = \frac{a}{b}$ C、 $\frac{a^{2}}{b^{2}} = \frac{a}{b}$ D、 $\frac{\frac{1}{2} a}{\frac{1}{2} b} = \frac{a}{b}$

查看试题解析
8. 用反证法证明“a＞b”时应假设（　　）

A、a＞b B、a＜b C、a=b D、a≤b

查看试题解析
9. 下列式子：① ${(- 2)}^{- 2} = - \frac{1}{4}$ ；② $a^{2} \div a^{3} = a^{- 1}$ ；③ $3 a^{- 2} = \frac{1}{3 a^{2}}$ ；④ $7.02 \times 10^{- 4} = 0.0000702$ 其中正确的式子有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 某煤厂原计划x天生产120吨煤，由于采用新的技术，每天增加生产3吨，因此提前2天完成任务，列出方程为（）

A、 $\frac{120}{x - 2} = \frac{120}{x} - 3$ B、 $\frac{120}{x} = \frac{120}{x + 2} - 3$ C、 $\frac{120}{x + 2} = \frac{120}{x} - 3$ D、 $\frac{120}{x} = \frac{120}{x - 2} - 3$

查看试题解析

二、填空题

11. 计算： $2 x^{2} y^{3} \div x y^{2} =$ .

查看试题解析
12. 如图，已知△ABC是等边三角形，BC=BD，∠CBD=90°，则∠1的度数是.

查看试题解析
13. 用科学记数法表示 $0.00021 =$ ；用小数表示 $3.57 \times 10^{- 6} =$

查看试题解析
14. 如图，在△ABC中，点D在边BC上，AB＝AD＝DC ， ∠C＝35°，则∠BAD＝度．

查看试题解析
15. 化简的 $(\frac{1}{x - 3} - \frac{x + 1}{x^{2} - 1}) \cdot (x - 3)$ 结果是．

查看试题解析
16. 如图，△ABC中，EF是AB的垂直平分线，与AB交于点D，BF=12，CF=3，则AC = ．

查看试题解析
17. 用换元法解方程 $\frac{x^{2} - 12}{x} - \frac{4 x}{x^{2} - 12} = 3$ 时，设 $\frac{x^{2} - 12}{x} = y$ ，则原方程可化为

查看试题解析
18. 若 $\frac{1}{(2 n - 1) (2 n + 1)}$ = $\frac{a}{2 n - 1}$ + $\frac{b}{2 n + 1}$ ，对任意自然数n都成立，则a= ， b=；
计算：m= $\frac{1}{1 \times 3}$ + $\frac{1}{3 \times 5}$ + $\frac{1}{5 \times 7}$ + …+ $\frac{1}{19 \times 21}$ = ．

查看试题解析

三、解答题

19. 计算：

(1)、 $2^{- 5} \times {(\frac{1}{2})}^{- 4} + 2^{- 1} \times 2 + {(π - 3.14)}^{0}$

(2)、 $\frac{x^{2} - 1}{x^{2} + 2 x + 1} \div \frac{x^{2} - x}{x + 1}$

查看试题解析
20. 解下列分式方程：

(1)、 $\frac{3 + x}{4 - x} = \frac{1}{2}$

(2)、 $\frac{2}{y + 1} + \frac{3}{y - 1} = \frac{6}{y^{2} - 1}$

查看试题解析
21. 先化简，再求值：

(1)、先化简，再求值： $\frac{x - 2}{x}$ ÷(x－ $\frac{4}{x}$ )，其中x＝ $\sqrt{2}$ －2.

(2)、先化简 $\frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ÷ $\frac{x^{2} - 2 x}{x + 1}$ ＋ $\frac{1}{x - 1}$ ，再从－2，－1，0，1，2中选一个合适的数作为x的值代入求值．

查看试题解析
22. 如图，在△ABC中，D是BC边上一点，AD=BD=AC，∠BAC=63⁰ ，求∠DAC的度数.

查看试题解析
23. 如图所示，已知AB＝AC＝20 cm，DE垂直平分AB，垂足为E，DE交AC 于点D，若△DBC的周长为35 cm，求BC的长．

查看试题解析
24. 李老师家距学校1900米，某天他步行去上班，走到路程的一半时发现忘带手机，此时离上班时间还有23分钟，于是他立刻步行回家取手机，随后骑电瓶车返回学校．已知李老师骑电瓶车到学校比他步行到学校少用20分钟，且骑电瓶车的平均速度是步行速度的5倍，李老师到家开门、取手机、启动电瓶车等共用4分钟.

(1)、求李老师步行的平均速度；

(2)、请你判断李老师能否按时上班，并说明理由.

查看试题解析
25. 已知：△ABC中，∠C=90°，CA=CB ，点D是AB的中点

(1)、如图，当点E在AC边上，ED⊥DF交BC所在的直线于点F ，求证：AE+BF=BC；

(2)、当E运动到CA的延长线上时，请画出相应的图形并判断（1）中的结论是否成立，若不成立，请写出相应的结论并证明．

查看试题解析