山东省淄博市沂源县2021-2022学年八年级上学期期中数学试题

试卷更新日期：2021-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中从左到右的变形，是因式分解的是（）

A、（a+3）（a-3）=a²-9 B、x²+x-5=（x-2）（x+3）+1 C、a²b+ab²=ab（a+b） D、x²+1=x（x+ $\frac{1}{x}$ ）

查看试题解析
2. 下列各式的因式分解中正确的是（）

A、 $- a^{2} + a b - a c = - a (a + b - c)$ B、 $9 x y z - 6 x^{2} y^{2} = 3 x y z (3 - 2 x y)$ C、 $3 a^{2} x - 6 b x + 3 x = 3 x (a^{2} - 2 b)$ D、 $\frac{1}{2} x y^{2} + \frac{1}{2} x^{2} y = \frac{1}{2} x y (x + y)$

查看试题解析
3. 下列计算错误的是（）

A、 $\frac{0.2 a + b}{0.7 a - b} = \frac{2 a + b}{7 a - b}$ B、 $\frac{x^{3} y^{2}}{x^{2} y^{3}} = \frac{x}{y}$ C、 $\frac{a - b}{b - a} = - 1$ D、 $\frac{1}{c} + \frac{2}{c} = \frac{3}{c}$

查看试题解析
4. 若方程 $\frac{x}{x - 3} - 2 = \frac{k}{x - 3}$ 有增根，则k的值等于（）

A、－2 B、0 C、1 D、3

查看试题解析
5. 将多项式 $4 x^{2} + 1$ 加上一个单项式后，使它能成为另一个整式的完全平方，下列添加单项式错误的是（）

A、4x B、 $- 4 x$ ⁴ C、 $4 x$ ⁴ D、 $- 4 x$

查看试题解析
6. 计算：85²﹣15²=（　　）

A、70 B、700 C、4900 D、7000

查看试题解析
7. 下列各式中，不能用平方差公式分解因式的是（）

A、 $- a^{2} + b^{2}$ B、 $- x^{2} - y^{2}$ C、 $49 x^{2} y^{2} - z^{2}$ D、 $16 m^{4} - 25 m^{2} p^{2}$

查看试题解析

8. 一城市准备选购一千株高度大约为2m的某种风景树来进行街道绿化，有四个苗圃生产基地投标（单株树的价格都一样）．采购小组从四个苗圃中都任意抽查了20株树苗的高度，得到的数据如下：

	树苗平均高度（单位：m）	标准差
甲苗圃	1.8	0.2
乙苗圃	1.8	0.6
丙苗圃	2.0	0.6
丁苗圃	2.0	0.2

请你帮采购小组出谋划策，应选购（）

A、甲苗圃的树苗 B、乙苗圃的树苗； C、丙苗圃的树苗 D、丁苗圃的树苗

查看试题解析

9. 2013年，某市发生了严重干旱，该市政府号召居民节约用水，为了解居民用水情况，在某小区随机抽查了10户家庭的月用水量，结果统计如图，则关于这10户家庭的月用水量，下列说法错误的是（　　）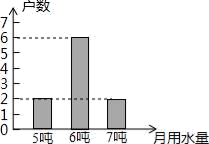

A、众数是6 B、极差是2 C、平均数是6 D、方差是4

查看试题解析
10. 某工地调来144人参加挖土和运土，已知3人挖出的土1人恰好能全部运走，怎样调配劳动力才使挖出来的土能及时运走且不窝工（停工等待）？为解决此问题，可设派 $x$ 人挖土，其他人运土，下列所列方程：① $\frac{144 - x}{x} = \frac{1}{3}$ ；② $144 - x = \frac{x}{3}$ ；③ $x + 3 x = 144$ ；④ $\frac{x}{144 - x} = 3$ ．正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. $a$ 、 $b$ 为实数，且 $a b = 1$ ，设 $P = \frac{a}{a + 1} + \frac{b}{b + 1}$ ， $Q = \frac{1}{a + 1} + \frac{1}{b + 1}$ ，则 $P$ 和 $Q$ 的大小关系是（）

A、 $P > Q$ B、 $P < Q$ C、 $P = Q$ D、不能确定

查看试题解析
12. 某人往返于 $A$ ， $B$ 两地，去时先步行2公里再乘汽车10公里；回来时骑自行车，来去所用时间恰好一样，已知汽车每小时比步行多走16公里，汽车比骑自行车每小时多走8公里，若步行速度为x公里/小时，则可列出方程（）

A、 $\frac{2}{x} + \frac{12}{x + 8} = \frac{10}{x + 16}$ B、 $\frac{10}{x + 16} - \frac{12}{x + 8} = \frac{2}{x}$ C、 $\frac{2}{x} + \frac{10}{x + 16} = \frac{12}{x + 8}$ D、 $\frac{10}{x + 16} + \frac{12}{x + 8} = \frac{2}{x}$

查看试题解析

二、填空题

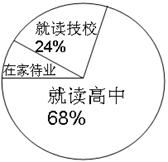
13. 某校对去年毕业的350名学生的毕业去向进行跟踪调查，并绘制出扇形统计图（如图所示），则该校去年毕业生在家待业人数有人．

查看试题解析
14. 有一组数据如下：2，3，a，5，6，它们的平均数是4，则这组数据的方差是.

查看试题解析
15. 若 $a x^{2} + 24 x + b = {(m x - 3)}^{2}$ ，则 $a =$ ．

查看试题解析
16. 已知 $x$ 为整数，且 $\frac{2}{x + 3} + \frac{2}{3 - x} + \frac{2 x + 18}{x^{2} - 9}$ 为整数，则所有符合条件的 $x$ 值的和为．

查看试题解析
17. 若关于x的方程 $\frac{a x}{x - 2}$ = $\frac{4}{x - 2}$ +1无解，则a的值是．

查看试题解析

三、解答题

18. 因式分解

(1)、 $- 12 x y + x^{2} + 36 y^{2}$

(2)、 $m n (m - n) - m (n - m)$

(3)、 $- 4 x^{3} + 20 x^{2} - 24 x$

查看试题解析
19. 计算

(1)、 $\frac{2 a - 2 b}{a^{2} - 2 a b + b^{2}} + \frac{1}{a - b}$

(2)、 $\frac{2}{x - 1} \div (\frac{2}{x^{2} - 1} + \frac{1}{x + 1})$

查看试题解析
20. 解分式方程

(1)、 $\frac{x}{x + 2} = \frac{x - 1}{x}$

(2)、 $\frac{1}{x - 2} = \frac{1 - x}{2 - x} - 3$

查看试题解析
21. 请你阅读下列计算过程，再回答所提出的问题：
解： $\frac{x - 3}{x^{2} - 1} - \frac{3}{1 - x}$

= $\frac{x - 3}{(x + 1) (x - 1)} - \frac{3}{x - 1}$ （A）

= $\frac{x - 3}{(x + 1) (x - 1)} - \frac{3 (x - 3)}{(x + 1) (x - 1)}$ （B）

=x﹣3﹣3（x+1）（C）

=﹣2x﹣6（D）

(1)、上述计算过程中，从哪一步开始出现错误：；

(2)、从B到C是否正确，若错误，错误的原因是；

(3)、请你正确解答．

查看试题解析
22. 某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了15人某月的加工零件个数：
加工件数
540
450
300
240
210
120
人数
1
1
2
6
3
2

(1)、写出这15人该月加工零件数的平均数、中位数和众数．

(2)、假如生产部负责人把每位工人的月加工零件数定为260（件），你认为这个定额是否合理，为什么？

查看试题解析
23. 国家实施高效节能电器的财政补贴政策，某款空调在政策实施后，客户每购买一台可获补贴500元.若同样用11万元所购买此款空调，补贴后可购买的台数比补贴前多20%，则该款空调补贴前的售价为每台多少元？

查看试题解析
24. （探索发现）
先观察下面给出的等式，探究其隐含的规律，然后回答问题： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ； $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ； $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ； $\dots$

(1)、若 $n$ 为正整数，直接写出结果： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{n (n + 1)} =$ ．

(2)、（拓展延伸）
根据上面探索的规律，解决下面的问题：

解关于 $x$ 的分式方程： $\frac{1}{(x - 1) (x - 2)} - \frac{1}{(x - 2) (x - 3)} - \frac{2}{(x - 1) (x - 3)} = \frac{x - 5}{x - 3}$ ．

查看试题解析

加工件数	540	450	300	240	210	120
人数	1	1	2	6	3	2