山东省烟台市龙口市2021-2022学年八年级上学期期中数学试题

试卷更新日期：2021-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式从左到右的变形中，是因式分解的为（）

A、a（x+y）=ax+ay B、6x³y²=2x²y•3xy C、t²﹣16+3t=（t+4）（t﹣4）+3t D、y²﹣6y+9=（y﹣3）²

查看试题解析
2. 如果把分式 $\frac{2 x}{3 x - 2 y}$ 中的x，y都扩大2倍，那么分式的值（）

A、扩大2倍 B、不变 C、缩小2倍 D、扩大4倍

查看试题解析
3. 下列分式是最简分式的是（）

A、 $\frac{2 x}{x^{2} + 2}$ B、 $\frac{x + 1}{x^{2} - 1}$ C、 $\frac{4}{2 x}$ D、 $\frac{2 - x}{x - 2}$

查看试题解析
4. 用计算器计算方差时，要首先进入统计计算状态，需要按键（）

A、 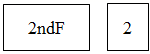B、 C、 D、

查看试题解析
5. 已知ab＝﹣2，a+b＝3，则a²b+ab²的值是（）

A、6 B、﹣6 C、1 D、﹣1

查看试题解析
6. 计算 $(x^{2} - x y) \div \frac{x - y}{x}$ 的结果是（）

A、 $x^{2}$ B、 $x^{2} - y$ C、 ${(x - y)}^{2}$ D、 $x$

查看试题解析
7. 如图，在6×6方格中有两个涂有阴影的图形M、N，①中的图形M平移后位置如②所示，以下对图形M的平移方法叙述正确的是（）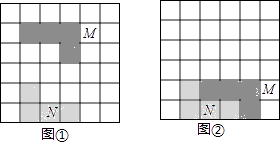

A、向右平移2个单位，向下平移3个单位 B、向右平移1个单位，向下平移3个单位 C、向右平移1个单位，向下平移4个单位 D、向右平移2个单位，向下平移4个单位

查看试题解析
8. 小明同学对数据15，28，36，4□，43进行统计分析，发现其中一个两位数的个位数字被黑水涂污看不到了，则统计结果与被涂污数字无关的是（）

A、平均数 B、标准差 C、中位数 D、极差

查看试题解析
9. 某船在静水中航行的速度是x千米/时，水流的速度是y千米/时，该船从甲地顺流去乙地a小时到达，则该船从乙地返回甲地需要的时间为（）

A、 $\frac{a (x + y)}{x - y}$ 小时 B、 $\frac{a (x - y)}{x + y}$ 小时 C、 $\frac{a x}{x + y}$ 小时 D、 $\frac{a (x + y)}{y - x}$ 小时

查看试题解析
10. 小亮家1月至10月的用电量统计如图所示，这组数据的众数和中位数分别是（）

A、30和 20 B、30和25 C、30和22.5 D、30和17.5

查看试题解析
11. 某班有50人，一次数学测试后，老师对测试成绩进行了统计．由于小颖没有参加此次集体测试，因此计算其他49人的平均分为92分，方差s²＝23．后来小颖进行了补测，成绩是92分，关于该班50人的数学测试成绩，下列说法正确的是（）

A、平均分不变，方差变小 B、平均分不变，方差变大 C、平均分和方差都不变 D、平均分和方差都改变

查看试题解析
12. 若关于x的方程 $\frac{m - 1}{x - 1} = 2$ 的解为正数，则m的取值范围是（）

A、 $m > - 1$ B、 $m \neq 1$ C、 $m > 1$ D、 $m > - 1$ 且 $m \neq 1$

查看试题解析

二、填空题

13. 若分式 $\frac{| x | - 3}{x - 3}$ 的值为零，则x= ．

查看试题解析
14. 当 $m =$ 时，解分式方程 $\frac{x - 5}{x - 3} = \frac{m}{3 - x}$ 会出现增根．

查看试题解析
15. 某班同学进行知识竞赛，将所得成绩整理成如图所示的统计图，则这次竞赛成绩的众数是分．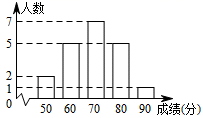

查看试题解析
16. 若二次三项式x $^{2}$ +kx+81是一个完全平方式，则k的值是．

查看试题解析
17. 如图，将 $△$ ABC沿射线BC方向移动，使点B移动到点C ，得到 $△$ DCE ，连接AE ，与DC交于点F ，若 $△$ ABC的面积为6，则 $△$ ACF的面积为．

查看试题解析
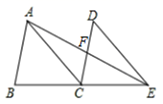18. 如图，边长为2m+3的正方形纸片剪出一个边长为m+3的正方形之后，剩余部分可剪拼成一个长方形，若拼成的长方形一边长为m，则另一边长为

查看试题解析

三、解答题

19. 分解因式：

(1)、-2a³b+6a²b-8ab ．

(2)、（x+y）（x﹣y）+y（y﹣x）

(3)、（3a+2b）²﹣（2a+3b）² ．

(4)、（n²+2n+2）（n²+2n）+1．

查看试题解析
20.

(1)、计算： $\frac{2 a}{a^{2} - 16} - \frac{1}{a - 4}$

(2)、 $(\frac{1}{a - 2} + a) \div \frac{a^{2} - a}{a - 2}$

(3)、先化简 $\frac{2 a + 2}{a - 1} \div (a + 1) + \frac{a^{2} - 1}{a^{2} - 2 a + 1}$ ，然后a在-1，1，2三个数中任选一个合适的数代入求值．

查看试题解析
21. 解方程： $\frac{2}{x^{2} - 1} + 1 = \frac{x}{x - 1}$ ．

查看试题解析
22. 某公司招聘人才，对应聘者分别进行了阅读能力、思维能力和表达能力三项测试，其中甲、乙两人的测试成绩（百分制）如下表：（单位：分）

应聘者

阅读能力

思维能力

表达能力

甲

85

90

80

乙

95

80

95

(1)、若根据三项测试的平均成绩在甲、乙两人中录用一人，那么谁将被录用？

(2)、若将阅读能力、思维能力和表达能力三项测试得分按1：3：1的比确定每人的最后成绩，谁将被录用？

查看试题解析
23. 为了弘扬我国书法艺术，培养学生良好的书写能力．某校举办了书法比赛，学校准备为获奖同学颁奖，在购买奖品时发现， $A$ 种奖品的单价比 $B$ 种奖品的单价多10元，用300元购买 $A$ 种奖品的件数与用240元购买 $B$ 种奖品的件数相同．

(1)、求 $A$ ， $B$ 两种奖品的单价各是多少元；

(2)、学校为获奖的15名学生购买奖品（每人一件 $A$ 种奖品或一件 $B$ 种奖品），且购买的总费用不超过700元，求最多可以购买多少件 $A$ 种奖品？

查看试题解析

24. 表格是小明一学期数学成绩的记录，根据表格提供的信息回答下面的问题．

考试类别	平时				期中考试	期末考试
考试类别	第一单元	第二单元	第三单元	第四单元	期中考试	期末考试
成绩	88	92	90	86	90	96

(1)、小明6次成绩的众数是分；中位数是分；

(2)、计算小明平时成绩的平均分；

(3)、计算小明平时成绩的方差；

(4)、按照学校规定，本学期的综合成绩的权重如图所示，请你求出小明本学期的综合成绩，要写出解题过程．（注意：①平时成绩用四次成绩的平均数；②每次考试满分都是100分）．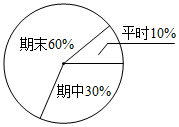

查看试题解析

25. 某校“数学社团”活动中，小亮对多项式进行因式分解，m²－mn+2m－2n =(m²－mn)+(2m－2n)=m(m－n)+2(m－n) =(m－n)(m+2)．以上分解因式的方法叫做“分组分解法”，请你在小亮解法的启发下，解决下面问题：

(1)、因式分解a³－3a²－9a+27；

(2)、因式分解x²+4y²－4xy－16；

(3)、已知a ， b ， c是 $△$ ABC的三边，且满足 $a^{2} - a b + c^{2} = 2 a c - b c$ ，判断 $△$ ABC的形状并说明理由．

查看试题解析
26. （阅读学习）
阅读下面的解题过程：

已知： $\frac{x}{x^{2} + 1} = \frac{1}{3}$ ，求 $\frac{x^{2}}{x^{4} + 1}$ 的值．

解：由 $\frac{x}{x^{2} + 1} = \frac{1}{3}$ 知x≠0，所以 $\frac{x^{2} + 1}{x} = 3$ ，即 $x + \frac{1}{x} = 3$

所以 $\frac{x^{4} + 1}{x^{2}} = x^{2} + \frac{1}{x^{2}} = {(x + \frac{1}{x})}^{2} - 2 = 3^{2} - 2 = 7$

故 $\frac{x^{2}}{x^{4} + 1}$ 的值为 $\frac{1}{7}$ ．

（类比探究）

(1)、上题的解法叫做“倒数法”，请你利用“倒数法”解决下面的题目：已知 $\frac{x}{x^{2} - 3 x + 1} = - 1$ ，求 $\frac{x^{2}}{x^{4} - 7 x^{2} + 1}$ 的值．

(2)、（拓展延伸）
已知 $\frac{1}{a} + \frac{1}{b} = \frac{1}{6}$ ， $\frac{1}{b} + \frac{1}{c} = \frac{1}{9}$ ， $\frac{1}{a} + \frac{1}{c} = \frac{1}{15}$ ，求 $\frac{a b c}{a b + b c + a c}$ 的值．

查看试题解析

应聘者	阅读能力	思维能力	表达能力
甲	85	90	80
乙	95	80	95