山东省临沂市平邑县2021-2022学年八年级上学期期中数学试题
试卷更新日期:2021-12-01 类型:期中考试
一、单选题
-
1. 下列图形是轴对称图形的有( )
 A、2个 B、3个 C、4个 D、5个2. 在△ABC中,若∠A+∠B-∠C=0,则△ABC是( )A、直角三角形 B、锐角三角形 C、钝角三角形 D、等腰三角形3. 做一个三角形的木架,以下四组木棒中,符合条件的是( )A、3,4,7 B、4,5,6 C、5,12,6 D、1,2,34. 已知:点 与点 关于 轴对称,则 的值为( )A、0 B、1 C、-1 D、5. 一个正多边形的内角和为720°,则这个正多边形的每一个外角等于( )A、50° B、60° C、70° D、80°6. 已知,如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的有( )
A、2个 B、3个 C、4个 D、5个2. 在△ABC中,若∠A+∠B-∠C=0,则△ABC是( )A、直角三角形 B、锐角三角形 C、钝角三角形 D、等腰三角形3. 做一个三角形的木架,以下四组木棒中,符合条件的是( )A、3,4,7 B、4,5,6 C、5,12,6 D、1,2,34. 已知:点 与点 关于 轴对称,则 的值为( )A、0 B、1 C、-1 D、5. 一个正多边形的内角和为720°,则这个正多边形的每一个外角等于( )A、50° B、60° C、70° D、80°6. 已知,如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的有( )
⑴AD平分∠EDF;
⑵△EBD≌△FCD;
⑶BD=CD;
⑷AD⊥BC.
A、1个 B、2个 C、3个 D、4个7.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
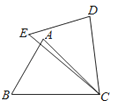 A、BC=EC,∠B=∠E B、BC=EC,AC=DC C、BC=DC,∠A=∠D D、∠B=∠E,∠A=∠D8. 如图,在 中, 的平分线与 的垂直平分线交于点 ,连接 ,若 , ,则 的度数为( )
A、BC=EC,∠B=∠E B、BC=EC,AC=DC C、BC=DC,∠A=∠D D、∠B=∠E,∠A=∠D8. 如图,在 中, 的平分线与 的垂直平分线交于点 ,连接 ,若 , ,则 的度数为( ) A、12° B、31° C、53° D、75°9. 如图,三角形纸片ABC , AB=12cm , BC=8cm , AC=7cm , 沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD , 则△AED的周长为( )cm .
A、12° B、31° C、53° D、75°9. 如图,三角形纸片ABC , AB=12cm , BC=8cm , AC=7cm , 沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD , 则△AED的周长为( )cm . A、10 B、11 C、13 D、1510. 下列说法中,正确说法的个数有( )
A、10 B、11 C、13 D、1510. 下列说法中,正确说法的个数有( )①角是轴对称图形,对称轴是角的平分线;②等腰三角形至少有 条对称轴,至多有 条对称轴;③关于某直线对称的两个三角形一定是全等三角形;④两图形关于某直线对称,对称点一定在直线的两旁.
A、1个 B、2个 C、3个 D、4个11. 已知非直角三角形ABC中,∠A=45°,高BD与CE所在直线交于点H,则∠BHC的度数是( )A、45° B、45° 或135° C、45°或125° D、135°12. 如图, , , ,结论:① ;② ;③ ;④ .其中正确的有( ) A、①②④ B、①③④ C、②③④ D、①②③④
A、①②④ B、①③④ C、②③④ D、①②③④二、填空题
-
13. 如图,工程建筑中的屋顶钢架经常采用三角形的结构,其中的数学道理是三角形具有性.
 14. 已知等腰三角形的一个外角为 ,则它的顶角的度数为 .15. 如图,在 中, 分别以 为圆心, 为半径画弧交于两点,过这两点的直线交AC于点,连接BD,则△BCD的周长是 .
14. 已知等腰三角形的一个外角为 ,则它的顶角的度数为 .15. 如图,在 中, 分别以 为圆心, 为半径画弧交于两点,过这两点的直线交AC于点,连接BD,则△BCD的周长是 . 16. 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上的 处,折痕为CD , 则 = .
16. 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上的 处,折痕为CD , 则 = . 17. 在平面直角坐标系中,点A(2,0),B(0,1),当点C的坐标为 时,△BOC与△ABO全等.
17. 在平面直角坐标系中,点A(2,0),B(0,1),当点C的坐标为 时,△BOC与△ABO全等.三、解答题
-
18. 如下图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第 个图形需要黑色棋子的个数是 .
 19. 如图,已知AD、AE分别是△ABC的高和中线,AB=3 cm,AC=4cm,BC=5cm,∠BAC=90°.
19. 如图,已知AD、AE分别是△ABC的高和中线,AB=3 cm,AC=4cm,BC=5cm,∠BAC=90°.
试求:
(1)、△ABE的面积;(2)、AD的长度;20. 如图, 三个顶点的坐标分别为 , , .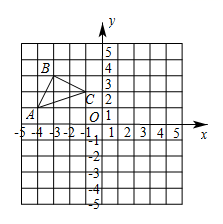 (1)、作出 关于 轴对称的 ,并写出 的坐标.(2)、求出 的面积.(3)、在 轴上画出点 ,使 最小,并写出点 的坐标.(不写作法,保留作图痕迹)21. 如图,已知在 中, , 为 边的中点,过点 作 , ,垂足分别为 , .
(1)、作出 关于 轴对称的 ,并写出 的坐标.(2)、求出 的面积.(3)、在 轴上画出点 ,使 最小,并写出点 的坐标.(不写作法,保留作图痕迹)21. 如图,已知在 中, , 为 边的中点,过点 作 , ,垂足分别为 , . (1)、求证: ;(2)、若 , ,求 的周长.22. 如图,已知:在△ABC和△AEF中,点E在BC边上,AE=AB , AC=AF , ∠CAF=∠BAE , EF与AC交于点G .
(1)、求证: ;(2)、若 , ,求 的周长.22. 如图,已知:在△ABC和△AEF中,点E在BC边上,AE=AB , AC=AF , ∠CAF=∠BAE , EF与AC交于点G . (1)、求证:EF=BC;(2)、若∠ABC=65°.∠ACB=28°,求∠FGC的度数.23. 如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB , F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE . 连接DE、DF、EF .
(1)、求证:EF=BC;(2)、若∠ABC=65°.∠ACB=28°,求∠FGC的度数.23. 如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB , F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE . 连接DE、DF、EF . (1)、求证:△ADF≌△CEF;(2)、试证明△DFE是等腰直角三角形.24. 如图,已知 中, , , ,点 为 的中点.
(1)、求证:△ADF≌△CEF;(2)、试证明△DFE是等腰直角三角形.24. 如图,已知 中, , , ,点 为 的中点. (1)、如果点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上由点 向点 运动.
(1)、如果点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上由点 向点 运动.①若点 的运动速度与点 的运动速度相等,经过 秒后, 与 是否全等,请说明理由;
②若点 的运动速度与点 的运动速度不相等,当点 的运动速度为多少时,能够使 与 全等?
(2)、若点 以②中的运动速度从点 出发,点 以原来的运动速度从点 同时出发,都逆时针沿 三边运动,则经过后,点 与点 第一次在 的边上相遇?(在横线上直接写出答案,不必书写解题过程)